数据结构算法及应用——二叉树

一、二叉树性质

特性1 包含n (n> 0 )个元素的二叉树边数为n-1

特性2 二叉树的高度（height）或深度（depth）是指该二叉树的层数（有几层元素，而不是有层的元素间隔）

特性3 若二叉树的高度为h，h≥0，则该二叉树最少有h个元素，最多有(2^h – 1)个元素。

特性4 包含n 个元素的二叉树的高度最大为n，最小[log2 (n+1)]

二、满二叉树:

当高度为h 的二叉树恰好有2^h - 1个元素时，称其为满二叉树.

 

 

 

 

 

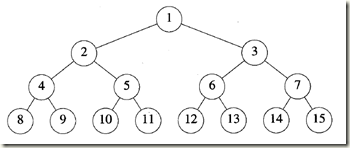
三、完全二叉树

假设对高度为h 的满二叉树中的元素按从第上到下，从左到右的顺序从1到2^h- 1进行编号（如图8 - 6所示）。假设从满二叉树中删除k个元素，其编号为2^h -i, 1≤i≤k，所得到的二叉树被称为完全二叉树.

注意满二叉树是完全二叉树的一个特例，并且，注意有n个元素的完全二叉树的深度为[log2 (n+1)]

特性5 设完全二叉树中一元素的序号为i, 1≤i≤n。则有以下关系成立：
1) 当i = 1时，该元素为二叉树的根。若i > 1，则该元素父节点的编号为  下取整【i/2】
2) 当2i >n时，该元素无左孩子。否则，其左孩子的编号为2i。
3) 若2i + 1 >n，该元素无右孩子。否则，其右孩子编号为2i + 1。

四、二叉树的遍历

• 前序遍历。
• 中序遍历。
• 后序遍历。
• 逐层遍历。

在进行前序遍历时，每个节点是在其左右子树被访问之前进行访问的；

在中序遍历时，首先访问左子树，然后访问子树的根节点，最后访问右子树。

在后序遍历时，当左右子树均访问完之后才访问子树的根节点。

五、源码

1.InterfaceBinaryTree 类

#pragma once
/*
T为BinaryTreeNode<U>类型的数据
*/
template<class T>
class InterfaceBinaryTree {
	//如果二叉树为空，则返回true ，否则返回false
	virtual bool IsEmpty() const=0;

	//返回二叉树的大小
	virtual int Size()const = 0;	

	//前序遍历
	virtual void PreOrder(void (*)(T *))const=0;   //参数是一个指向 void Func（T*)类型的函数指针

	//中序遍历
	virtual void InOrder(void(*)(T *))const=0;

	//后序遍历
	virtual void PostOrder(void(*)(T *))const=0;

	//逐层遍历
	virtual void LevelOrder(void(*)(T *))const=0;
};

2.BinaryTreeNode类

#pragma once
template<class T>
class BinaryTreeNode{
public:
	template<class  T> friend class BinaryTree;	

	BinaryTreeNode() {
		leftChild = rightChild = 0;
	}
	BinaryTreeNode(const T &data) {
		this->data = data;
		leftChild = rightChild = 0;
	}
	BinaryTreeNode(const T &data, BinaryTreeNode<T> *leftSubTree, BinaryTreeNode<T> *rightSubTree) {
		this->data = data;
		leftChild = leftSubTree;
		rightChild = rightSubTree;
	}

private:
	T data;
	BinaryTreeNode<T> *leftChild;
	BinaryTreeNode<T> *rightChild;

};

3.BinaryTree类

#pragma once
#include"BinaryTreeNode.h"
#include"InterfaceBinaryTree.h"
#include"MyException.h"
#include<iostream>
using namespace std;
template<class T>
class BinaryTree:public InterfaceBinaryTree<BinaryTreeNode<T>> {
public:
	BinaryTree() { root = 0; }
	~BinaryTree() {};
	//如果二叉树为空，则返回true ，否则返回false
	bool IsEmpty() const {
		return (root == 0) ? true : false;
	}
	//取根节点的数据域放入x；如果操作失败，则返回false，否则返回true
	bool Root(T &x)const;
	//创建一个二叉树，root作为根节点， left作为左子树，right作为右子树
	void MakeTree(const T &element, BinaryTree<T> &left, BinaryTree<T> &right);
	//拆分二叉树
	void BreakTree(T &element, BinaryTree<T> &left, BinaryTree<T> &right);

	void PreOrderOutput() const {
		PreOrder(output);
	}
	void InOrderOutput()const {
		InOrder(output);
	}
	void PostOrderOutput()const {
		PostOrder(output);
	}

	//前序遍历
	void PreOrder(void(*theVisit)(BinaryTreeNode<T>*))const {
		visit = theVisit; _preOrder(root);
	}
	//中序遍历
	void InOrder(void(*theVisit)(BinaryTreeNode<T>*))const {
		visit = theVisit; _inOrder(root);
	}
	//后序遍历
	void PostOrder(void(*theVisit)(BinaryTreeNode<T>*))const {
		visit = theVisit; _postOrder(root);
	}
	//逐层遍历
	void LevelOrder(void(*theVisit)(BinaryTreeNode<T>*))const {
		visit = theVisit; _levelOrder(root);
	}

	void Delete() {
		PostOrder(free);
		root = 0;
	}
	int Height()const {
		return height(root);
	}
	int Size()const {
		count = 0;
		InOrder(addCount);
		return count;
	}
protected:
	static void _preOrder(BinaryTreeNode<T> *root);
	static void _inOrder(BinaryTreeNode<T> *root);
	static void _postOrder(BinaryTreeNode<T> *root);
	static void _levelOrder(BinaryTreeNode<T> *root);

	static void(*visit)(BinaryTreeNode<T> *);          //函数指针，用于遍历时的函数访问
	static void output(BinaryTreeNode<T> *t) {
		cout << t->data << " ";
	}
	static void free(BinaryTreeNode<T> *t) {
		delete t;
	}
	static void addCount(BinaryTreeNode<T> *t) {
		count++;
	}
	static int height(BinaryTreeNode<T> *t);

private:
	BinaryTreeNode<T> *root;
	static int count;

};

//访问函数的函数指针
template<class T>
void(*BinaryTree<T>::visit)(BinaryTreeNode<T>*);
template<class T>
int BinaryTree<T>::count = 0;

//前序遍历
template<class T>
void BinaryTree<T>::_preOrder(BinaryTreeNode<T> *root) {
	if (root != 0) {
		BinaryTree<T>::visit(root);
		_preOrder(root->leftChild);
		_preOrder(root->rightChild);
	}
}
//中序遍历
template<class T>
void BinaryTree<T>::_inOrder(BinaryTreeNode<T> *root) {
	if (root != 0) {
		_inOrder(root->leftChild);
		BinaryTree<T>::visit(root);
		_inOrder(root->rightChild);
	}
}
//后序遍历
template<class T>
void BinaryTree<T>::_postOrder(BinaryTreeNode<T> *root) {
	if (root != 0) {
		_postOrder(root->leftChild);
		_postOrder(root->rightChild);
		BinaryTree<T>::visit(root);
	}
}
//逐层遍历
template<class T>
void BinaryTree<T>::_levelOrder(BinaryTreeNode<T> *root) {

}

//取根节点的数据域放入x；如果操作失败，则返回false，否则返回true
template<class T>
bool BinaryTree<T>::Root(T &x)const {
	if (root == 0) {
		return false;
	}
	x = root->data;
	return true;
}
/*生成一个二叉树，新建一个BinaryTreeNode节点，使其值为element，左子树为left，右子树为right*/
template<class T>
void BinaryTree<T>::MakeTree(const T &element, BinaryTree<T> &left, BinaryTree<T> &right) {
	root = new BinaryTreeNode<T>(element, left.root, right.root);
	left.root = right.root = 0;
}
/*将一个二叉树拆分成左子树和右子树两部分，根节点的值保存到element*/
template<class T>
void BinaryTree<T>::BreakTree(T &element, BinaryTree<T> &left, BinaryTree<T> &right) {
	if (root == 0)
		throw BadInput();
	element = root->data;
	left.root = root->leftChild;
	right.root = root->rightChild;
	delete root;                   //删除原来根节点的内存
	root = 0;
}
/*求二叉树的高度*/
template<class T>
int BinaryTree<T>::height(BinaryTreeNode<T> *t) {
	if (t == 0)
		return 0;
	int leftHeight = height(t->leftChild);   //左子树的高度
	int rightHeight = height(t->rightChild); //右子树的高度

	//返回左右子树中的最大值加一
	if (leftHeight > rightHeight)
		return ++leftHeight;
	else
		return ++rightHeight;
}

4.MyException类

#pragma once
#pragma once
// exception classes for various error types

#include<iostream>
#include <string>

using namespace std;

class NoMem {
public:
	NoMem() {
		this->message = "内存不足";
	}
	NoMem(string msg) {
		this->message = msg;
	}
	void OutputMessage() {
		cout << message << endl;
	}

private:
	string message;

};
class OutOfBounds {
public:
	OutOfBounds() {
		this->message = "输入超过了数组的界";
	}
	OutOfBounds(string msg) {
		this->message = msg;
	}
	void OutputMessage() {
		cout << message << endl;
	}

private:
	string message;

};
class BadInput {
public:
	BadInput() {
		this->message = "输入有误";
	}
	BadInput(string msg) {
		this->message = msg;
	}
	void OutputMessage() {
		cout << message << endl;
	}
private:
	string message;
};