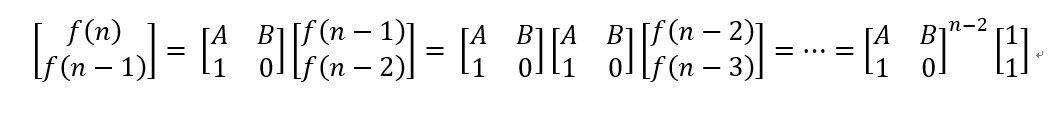HDU 1005 Number Sequence(矩阵快速幂,快速幂模板)
f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.
Given A, B, and n, you are to calculate the value of f(n).
以下是快速幂的模板, 求a^n, 为防止溢出,中间最好mod一哈
int main(){
int n;
int a;
cin >> a>>n;
int ans = 1;
while(n){//a^n
if(n&1){
ans *= a;
}
a*=a;
n>>=1;
ans %= 10000007;
}
cout << ans<<endl;
return 0;
}本题的递推式:
代码(含矩阵快速幂):
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<set>
#include<map>
#include<queue>
#include<cmath>
#include<stdlib.h>
typedef long long ll;
typedef unsigned long long ull;
using namespace std;
const int maxn = 1e5 + 100;
double eps = 1e-8;
int a[4][4], b[4][4];
int ans[4][4];
struct mtx{
int a[4][4];
};
mtx mtpl(mtx x, mtx y){//将矩阵a乘b的结果直接放在tmp里
mtx tmp;
memset(tmp.a, 0, sizeof(tmp.a));
for(int i = 1; i <= 2; i++){
for(int j = 1; j <= 2; j++){
int sum = 0;
for(int k = 1; k <= 2; k++){
sum += x.a[i][k] * y.a[k][j];
}
sum%=7;
tmp.a[i][j] += sum;
}
}
return tmp;
}
int main(){
int A, B;
ll n;
while(scanf("%d %d %lld", &A, &B, &n) ){
if(A==B && B==n && n==0)break;
mtx a, ans;
ans.a[1][1] = ans.a[2][2] = 1;
ans.a[1][2] = ans.a[2][1] = 0;
a.a[1][1] = A;
a.a[1][2] = B;
a.a[2][1] = 1;
a.a[2][2] = 0;
n-=2; //注意这里求的是a^(n-2)而不是a^n
if(n==-1) {
cout << 1<<endl;
continue;
}
while(n){
if(n&1)ans=mtpl(ans, a);
a=mtpl(a, a);
n>>=1;
}
cout << (ans.a[1][1]+ans.a[1][2]) %7<< endl;//人家说最后结果mod 7,WA的时候没想到这里要%7。。不是第一次了
}
return 0;
}HDU 1005 Number Sequence(矩阵快速幂,快速幂模板)的更多相关文章
- HDU - 1005 Number Sequence 矩阵快速幂
HDU - 1005 Number Sequence Problem Description A number sequence is defined as follows:f(1) = 1, f(2 ...
- HDU - 1005 -Number Sequence(矩阵快速幂系数变式)
A number sequence is defined as follows: f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) m ...
- HDU 1005 Number Sequence(数列)
HDU 1005 Number Sequence(数列) Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Jav ...
- HDU 1005 Number Sequence(数论)
HDU 1005 Number Sequence(数论) Problem Description: A number sequence is defined as follows:f(1) = 1, ...
- HDU 1005 Number Sequence【斐波那契数列/循环节找规律/矩阵快速幂/求(A * f(n - 1) + B * f(n - 2)) mod 7】
Number Sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)T ...
- HDU - 1005 Number Sequence (矩阵快速幂)
A number sequence is defined as follows: f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mo ...
- HDU 1005 Number Sequence(矩阵)
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission( ...
- HDU 1005 Number Sequence【多解,暴力打表,鸽巢原理】
Number Sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)T ...
- HDU 1005 Number Sequence
Number Sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)T ...
随机推荐
- 17.python自定义模块的导入方式
1.直接用import导入 最后运行main.py可以看到命令行窗口输出了一句:你好,这样就完成了. 2.通过sys模块导入自定义模块的路径path 3.在环境变量中找到自定义模块 这个方法原理就是利 ...
- java 实现敏感词(sensitive word)工具详解使用说明
sensitive-word 平时工作中,只要涉及到用户可以自由发言(博客.文档.论坛),就要考虑内容的敏感性处理. sensitive-word 基于 DFA 算法实现的高性能敏感词工具.工具使用 ...
- linux文件通配符
* #匹配任意字符 ? #匹配任意单个字符 ~ #当前用户家目录 ~user #用户user的家目录 ~+ #当前工作目录 ~- #前一个工作目录 [0-9] #匹配的数字范围 [a-z] #匹配小写 ...
- GoCenter助力Golang全速前进
一.背景 Go语言是Google开发的一种静态强类型.编译型.并发型,并具有垃圾回收功能的编程语言.为了方便搜索和识别,有时会将其称为Golang.自2009年11月Google正式宣布推出,成为开放 ...
- 存储过程带参数和sqlcommand
public DataSet SelectBillNo(string CarrierCode, string Date, string CompanyCode) { System.Collection ...
- BZOJ4559&P3270[JLoi2016]成绩比较
题目描述 \(G\)系共有\(n\)位同学,\(M\)门必修课.这\(N\)位同学的编号为\(0\)到\(N-1\)的整数,其中\(B\)神的编号为\(0\)号.这\(M\)门必修课编号为\(0\)到 ...
- kubernetes concepts -- Pod Lifecycle
Pod Lifecycle This page describes the lifecycle of a Pod. Pod phase A Pod’s status field is a PodSta ...
- 公司项目redis 项目报错 记事
异常内容: Timeout performing GET Key_CacheHSCode, inst: 1, mgr: ExecuteSelect, err: never, queue: 2, qu ...
- 「 从0到1学习微服务SpringCloud 」10 服务网关Zuul
系列文章(更新ing): 「 从0到1学习微服务SpringCloud 」06 统一配置中心Spring Cloud Config 「 从0到1学习微服务SpringCloud 」07 RabbitM ...
- 一题多解——Strategic Game
点击打开题目 题目大意:给定一棵无根树,点亮其中某些点,使得这棵树的所有边都连接着一个以上的点亮的点 贪心中比较有挑战的题 由于如果点亮叶节点,就只会照亮一条边,但点亮它的父亲,就可以照亮除此边以外的 ...