题解 LA3720

题目大意 多组数据，每组数据给定两个整数 \(n,m\)，请求出 \(n\times m\) 的点阵（即 \((n-1)\times(m-1)\) 的方格）中有多少条非水平竖直的经过至少两个格点的不同直线。

分析 这道题有多种解法，这里给出最经典的，使用容斥原理的解法。

令 \(dp[i][j]\) 表示 \(i\times j\) 的方格中，经过 \((0,0)\) 顶点的所有至少经过两个点的不同直线数（比如 \(dp[3][2]=5\)）。

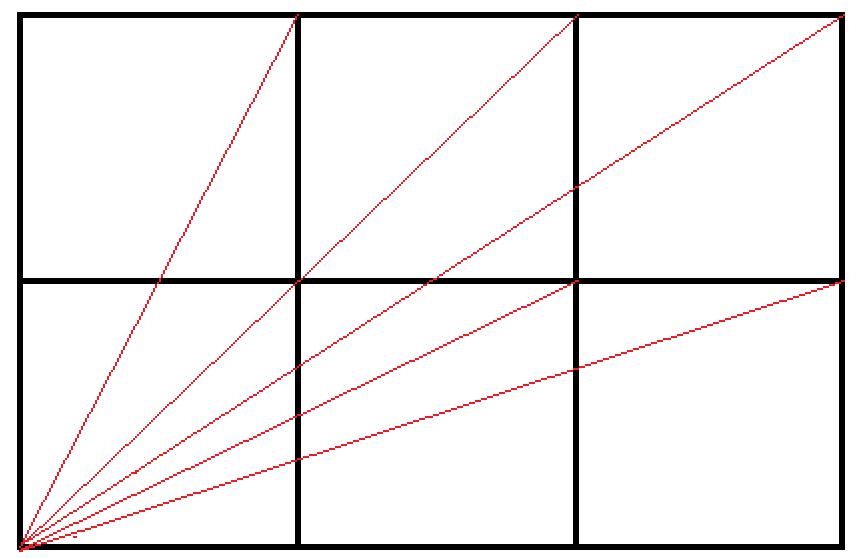
不难发现，\(dp\) 数组满足可加可减性，也即可以用容斥原理来递推。且点 \((i,j)\) 当且仅当 \(GCD(i,j)=1\) 时可以为 \(dp[i][j]\) 贡献 \(1\)。所以有

\[dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+[gcd(i,j)=1]
\]

现在考虑如何用 \(dp\) 数组来递推出最终答案。我们记 \(i\times j\) 方格中从左下到右上的不同直线数为 \(ans[i][j]\)，则最终答案为 \(2\times ans[i][j]\)（比如 \(ans[3][2]=14\)）。

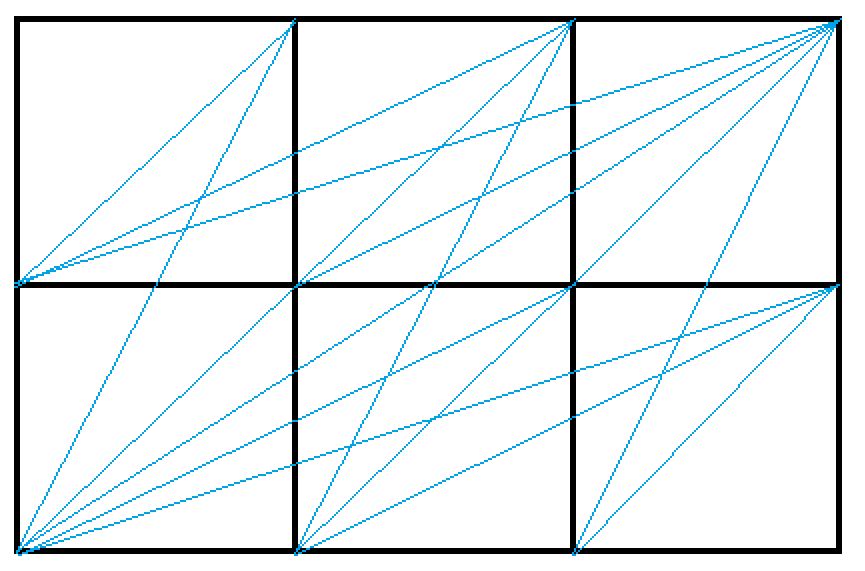
不难看出，\(ans\) 数组也满足可加可减性，可以用容斥原理来递推。且点 \((i,j)\) 构成的新直线当且仅当它在 \(dp[i][j]\) 中而不在 \(dp[i/2][j/2]\) 中才有贡献，这是因为如果它在被重复计算过则一定在 \(dp[i/2][j/2]\) 中被计算过（为什么），所以有

\[ans[i][j]=ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1]+dp[i][j]-dp[i/2][j/2]
\]

#include<bits/stdc++.h>
using namespace std;

const int maxn = 305;
const int maxm = 305;

int n, m;
int dp[maxn][maxm];
int ans[maxn][maxm];

void Init(int N, int M)
{
	for(int i = 1; i <= N; ++i)
		for(int j = 1; j <= M; ++j)
			dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + (__gcd(i, j) == 1);

	for(int i = 1; i <= N; ++i)
		for(int j = 1; j <= M; ++j)
			ans[i][j] = ans[i - 1][j] + ans[i][j - 1] - ans[i - 1][j - 1] + dp[i][j] - dp[i / 2][j / 2];
}

int main()
{
	Init(300, 300);
	while(~scanf("%d%d", &n, &m) && n && m)
		printf("%d\n", 2 * ans[n - 1][m - 1]);
}