【java面试】算法篇之堆排序

一、堆的概念

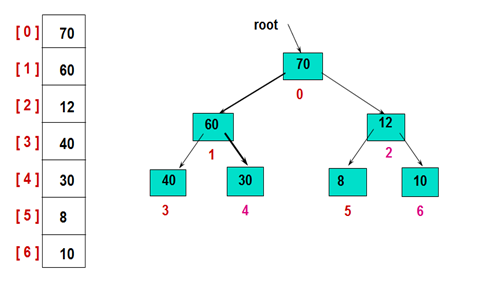
堆是一棵顺序存储的完全二叉树。完全二叉树中所有非终端节点的值均不大于（或不小于）其左、右孩子节点的值。

其中每个节点的值小于等于其左、右孩子的值，这样的堆称为小根堆；

其中每个节点的值大于等于其左、右孩子的值，这样的堆称为大根堆；

二、要点

1.将数组构造成初始堆（若想升序则建立大根堆，若想降序，则建立小根堆）

从最后一个节点开始调整，得到初始堆。

2.堆排序处理

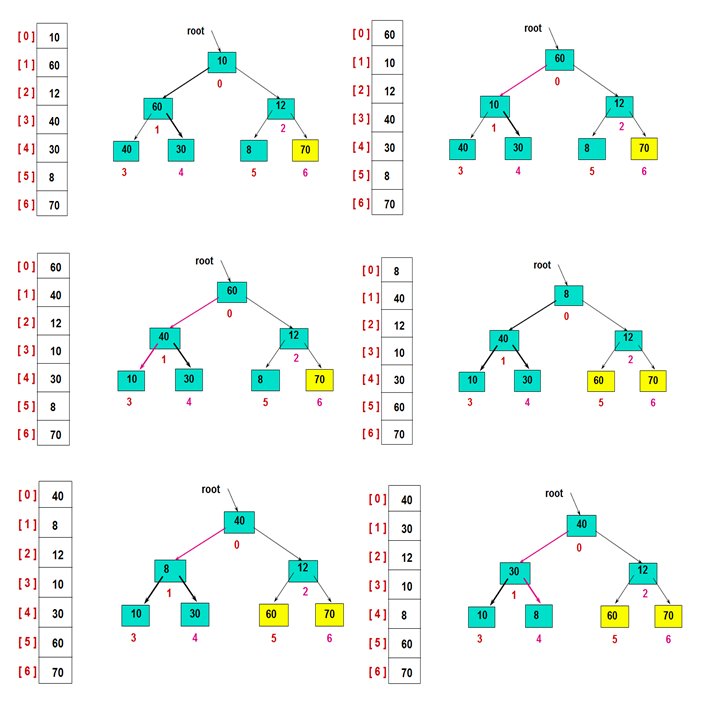
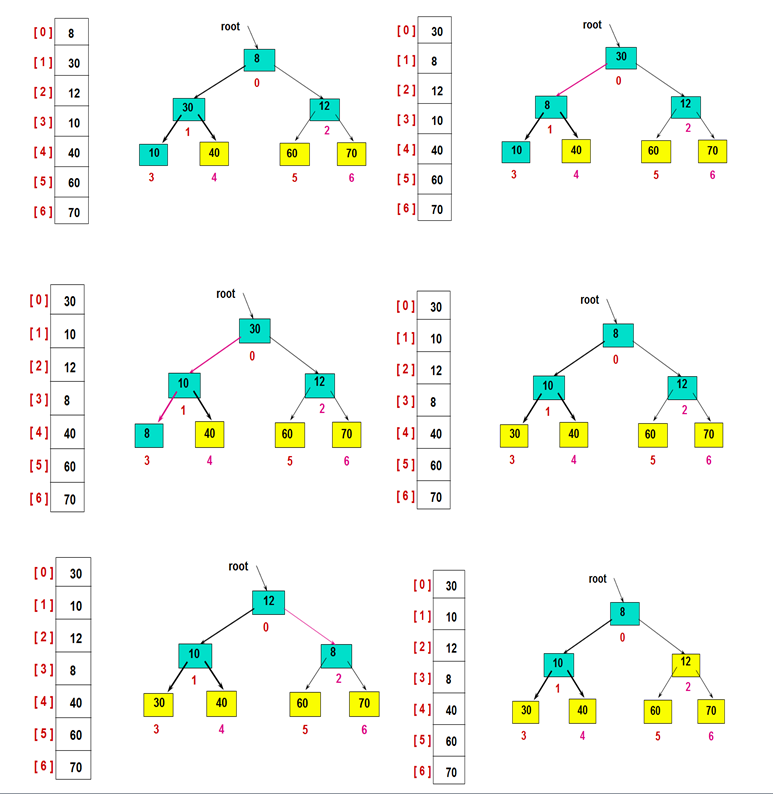
交换堆顶的元素和最后一个元素，此时最后一个位置作为有序区（有序区显示为黄色），然后进行其他无序区的堆调整，重新得到大顶堆后，交换堆顶和倒数第二个元素的位置……

重复此过程：

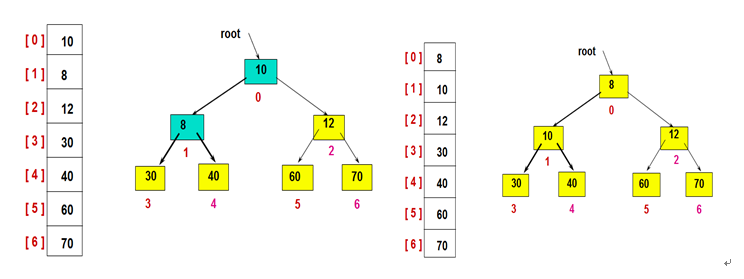
最后，有序扩展完成即排序完成：

核心代码

public void HeapAdjust(int[] array, int parent, int length) {

    int temp = array[parent]; // temp保存当前父节点

    int child = 2 * parent + 1; // 先获得左孩子

    while (child < length) {

        // 如果有右孩子结点，并且右孩子结点的值大于左孩子结点，则选取右孩子结点

        if (child + 1 < length && array[child] < array[child + 1]) {

            child++;

        }

        // 如果父结点的值已经大于孩子结点的值，则直接结束

        if (temp >= array[child])

            break;

        // 把孩子结点的值赋给父结点

        array[parent] = array[child];

        // 选取孩子结点的左孩子结点,继续向下筛选

        parent = child;

        child = 2 * child + 1;

    }

    array[parent] = temp;

}

public void heapSort(int[] list) {

    // 循环建立初始堆

    for (int i = list.length / 2; i >= 0; i--) {

        HeapAdjust(list, i, list.length - 1);

    }

    // 进行n-1次循环，完成排序

    for (int i = list.length - 1; i > 0; i--) {

        // 最后一个元素和第一元素进行交换

        int temp = list[i];

        list[i] = list[0];

        list[0] = temp;

        // 筛选 R[0] 结点，得到i-1个结点的堆

        HeapAdjust(list, 0, i);

        System.out.format("第 %d 趟: \t", list.length - i);

        printPart(list, 0, list.length - 1);

    }

}

算法分析

堆排序算法的总体情况

排序类别	排序方法	时间复杂度			空间复杂度	稳定性	复杂性
		平均情况	最坏情况	最好情况
选择排序	堆排序	O(nlog2n)	O(nlog2n)	O(nlog2n)	O(1)	不稳定	较复杂