CodeForce - 1187 E. Tree Painting (换根dp）

You are given a tree (an undirected connected acyclic graph) consisting of nn vertices. You are playing a game on this tree.

Initially all vertices are white. On the first turn of the game you choose one vertex and paint it black. Then on each turn you choose a white vertex adjacent (connected by an edge) to any black vertex and paint it black.

Each time when you choose a vertex (even during the first turn), you gain the number of points equal to the size of the connected component consisting only of white vertices that contains the chosen vertex. The game ends when all vertices are painted black.

Let's see the following example:

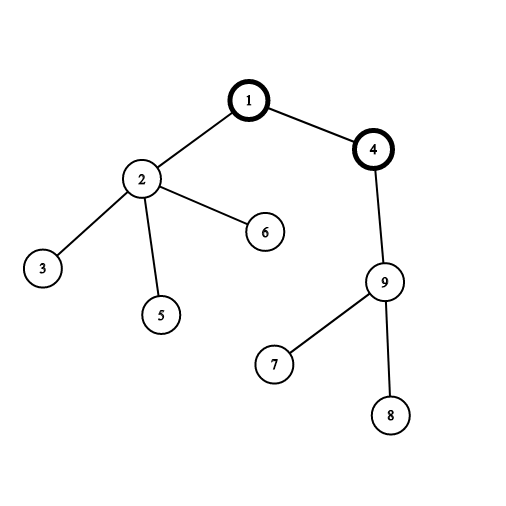
Vertices 11 and 44 are painted black already. If you choose the vertex 22, you will gain 44 points for the connected component consisting of vertices 2,3,52,3,5 and 66. If you choose the vertex 99, you will gain 33 points for the connected component consisting of vertices 7,87,8 and 99.

Your task is to maximize the number of points you gain.

Input

The first line contains an integer nn — the number of vertices in the tree (2≤n≤2⋅1052≤n≤2⋅105).

Each of the next n−1n−1 lines describes an edge of the tree. Edge ii is denoted by two integers uiui and vivi, the indices of vertices it connects (1≤ui,vi≤n1≤ui,vi≤n, ui≠viui≠vi).

It is guaranteed that the given edges form a tree.

Output

Print one integer — the maximum number of points you gain if you will play optimally.

Examples

input

Copy

9
1 2
2 3
2 5
2 6
1 4
4 9
9 7
9 8

output

Copy

36

input

Copy

5
1 2
1 3
2 4
2 5

output

Copy

14

题意：
要把树上每个节点染成黑色，每次只能选择染与黑色点相邻的点，第一次染色随意。
每次染色，所获贡献是，与当前点联通的白色点的个数，包括自身。

思路：
首先以1号节点为根节点，计算出每一个节点的子树大小(siz[i]) ,然后计算出每一个节点的所有子树siz之和（dp[i])。
假设当前根节点是u，子节点是v，那么u去掉v子树的贡献为 ：res = dp[u]-dp[v]-siz[v];
dp[v]就会变成 dp[v]=dp[v]+res+(n-siz[v])

#include<iostream>
#include<algorithm>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<ctime>

#define fuck(x) cout<<#x<<" = "<<x<<endl;
#define debug(a, x) cout<<#a<<"["<<x<<"] = "<<a[x]<<endl;
#define ls (t<<1)
#define rs ((t<<1)|1)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = ;
const int maxm = ;
const int inf = 0x3f3f3f3f;
const ll Inf = ;
const int mod = ;
const double eps = 1e-;
const double pi = acos(-);

int Head[maxn];
struct edge{
    int v;
    int Next;
}e[maxn];
int cnt=;
void add(int x,int y){
    e[cnt].v=y;
    e[cnt].Next = Head[x];
    Head[x]=cnt++;
}
ll dp[maxn];
ll siz[maxn];
bool vis[maxn];

int n;
void dfs(int u){
    vis[u]=true;
    for(int k=Head[u];~k;k=e[k].Next){
        if(vis[e[k].v]){ continue;}
        dfs(e[k].v);
        siz[u]+=siz[e[k].v];
        dp[u]+=dp[e[k].v];
    }
    siz[u]++;
    dp[u]+=siz[u];
}

void dfs1(int u){
    vis[u]=true;
    for(int k=Head[u];~k;k=e[k].Next){
        int v = e[k].v;
        if(vis[v]){ continue;}
        ll res = dp[u]-dp[v]-siz[v];
        dp[v]=dp[v]+res-siz[v]+n;
        dfs1(v);
    }
}

int main() {
//    ios::sync_with_stdio(false);
//    freopen("in.txt", "r", stdin);

    memset(Head,-,sizeof(Head));

    scanf("%d",&n);
    for(int i=;i<n;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }

    dfs();
    memset(vis,,sizeof(vis));
    dfs1();

    ll ans=;
    for(int i=;i<=n;i++){
//        printf("%lld ",siz[i]);
        ans = max(ans,dp[i]);
    }
//    printf("\n");
    printf("%lld\n",ans);
    return ;
}