机器学习实战-ch3-决策树

决策树是一种新算法：

优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。
缺点：可能会产生过度匹配问题。

决策树算法可用于数据类型：数值型和标称型。

决策树的核心在于选择正确的属性对数据进行划分。选择的标准是数据增益。信息增益：讲无序的数据变得更加有序。

信息增益熵：如果把X分成n个类，每个类的概率为p（i），那么-log（p（i））的期望就是熵。

如果分成1类，则熵为0，表示没有增益。

如果分成两类，各占1半，熵为1；

如果分成4类，各占1/4,则熵为2；

可以直观的感觉分成类越多，熵就越大。

---

[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]

按照最后一个属性划分，熵为0.97

加上一个元素[1,1,’maybe’]，熵就变成1.47

-----

为了计算数据增益，需要定义一个子函数。按照特定的维度，以及维度上的值，划分dataSet。

-----

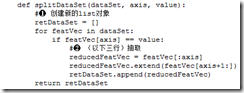
利用上面的子函数可以选择增益最大的维度。

对每个维度di进行遍历

对di上的value进行切分，得到k个集合

计算一个熵si

选择最大的si，对应的维度就是用来做决策的维度。

-----

每次选择一个维度后，对应的维度就会从数据集消失。然后dataSet分成若干个小集合。如果某个dataSet子集中所有元素label一致，则不需要再次划分。否则继续选择增益最大的属性继续划分。直到构成完整的决策树。