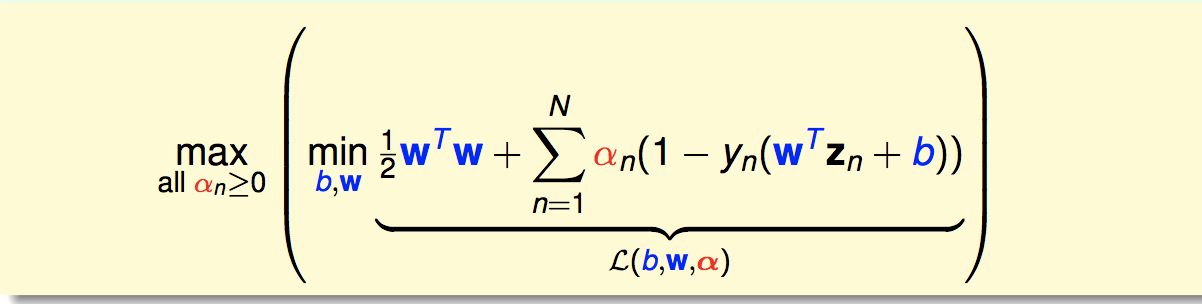对偶SVM
1.对偶问题的推导
为什么要求解对偶问题?一是对偶问题往往更容易求解,二是可以自然的引入核函数。
1.1 用拉格朗日函数将原问题转化为“无约束”等价问题
原问题是:

写出它的拉格朗日函数:

然后我们的原问题就等价为:

为什么可以这样等价:

即:对于不满足约束条件的(b,w),min里面趋于无穷大,因此min就把这些b,w舍去了;对于满足约束条件的解,min里面就刚好是原来的目标函数,刚好与原问题等价。
1.2 导出拉格朗日对偶问题
首先我们有如下成立:

然后我们取右边式子中的“best”阿尔法,仍然会有大于等于号成立,因为best is one of any:

这时右边的式子就是对偶问题。这里直接给出一个定理,当满足下面条件时(对于SVM来说刚好满足),原始问题和对偶问题的解是相同的:

并且它们的最优解满足KKT条件:
1.3 用KKT条件来简化对偶问题
我们的对偶问题现在是:
根据KKT条件,我们有:

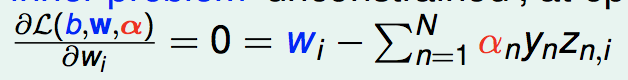
把第一个代进来:

再把第二个代进来:

这时候,我们的问题里面就只剩一个参数阿尔法了。再把平方项展开,写的好看一点,就得到了标准的硬间隔SVM对偶问题:

2. 解对偶问题
还是解QP那一套:

之后再求W和b:
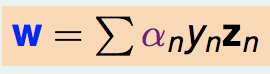 (所有支持向量的加权和)
(所有支持向量的加权和)
 (任取一个支持向量算出)
(任取一个支持向量算出)
3. 支持向量
引出对偶问题后,我们重现定义支持向量为阿尔法大于0的向量。他们一定是在边界上的,但是在边界上的不一定阿尔法大于0:

前面我们也提到过,w和b的计算只需要支持向量,其他向量都是无用的:

对偶SVM的更多相关文章
- 《机器学习技法》---对偶SVM
1.对偶问题的推导 为什么要求解对偶问题?一是对偶问题往往更容易求解,二是可以自然的引入核函数. 1.1 用拉格朗日函数将原问题转化为“无约束”等价问题 原问题是: 写出它的拉格朗日函数: 然后我们的 ...
- SVM原理与实践
SVM迅速发展和完善,在解决小样本.非线性及高维模式识别问题中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中.从此迅速的发展起来,已经在许多领域(生物信息学,文本和手写识别等)都取 ...
- SVM1 线性SVM
一.Linear Support Vector Machine 接下来的讨论假设数据都是线性可分的. 1.1 SVM的引入:增大对测量误差的容忍度 假设有训练数据和分类曲线如下图所示: 很明显,三个分 ...
- SVM学习笔记
一.SVM概述 支持向量机(support vector machine)是一系列的监督学习算法,能用于分类.回归分析.原本的SVM是个二分类算法,通过引入“OVO”或者“OVR”可以扩展到多分类问题 ...
- SVM对偶形式
dual svm 对偶SVM linear SVM 可以用二次规划方法解 xn通过非线性转换变成zn SVM配合非线性特征转换 透过large-margin降低模型复杂度 透过特征转换得到弯弯曲曲的边 ...
- SVM笔记
1.前言 SVM(Support Vector Machine)是一种寻求最大分类间隔的机器学习方法,广泛应用于各个领域,许多人把SVM当做首选方法,它也被称之为最优分类器,这是为什么呢?这篇文章将系 ...
- 【机器学习算法基础+实战系列】SVM
概述 支持向量机是一种二分类模型,间隔最大使它有别于感知机.支持向量机学习方法由简至繁的模型:线性可分支持向量机(linear support vector machine in linearly s ...
- SVM小白教程(2):拉格朗日对偶
在上一篇文章中,我们推导出了 SVM 的目标函数: \[ \underset{(\mathbf{w},b)}{\operatorname{min}} ||\mathbf{w}|| \\ \operat ...
- SVM系列之拉格朗日对偶
在学习SVM(Support Vector Machine) 支持向量机时,对于线性可分的分类样本求出的分类函数为: 其中,分类超平面可以表示为:
随机推荐
- [LeetCode] Excel Sheet Column Number 求Excel表列序号
Related to question Excel Sheet Column Title Given a column title as appear in an Excel sheet, retur ...
- D3D三层Texture纹理经像素着色器实现渲染YUV420P
简单记录一下这两天用Texture实现渲染YUV420P的一些要点. 在视频播放的过程中,有的时候解码出来的数据是YUV420P的.表面(surface)通过设置参数是可以渲染YUV420P的,但Te ...
- go reflect
package main import ( "fmt" "reflect" // 反射包 ) type User struct{ //结构体类型 Id int ...
- redis学习笔记
Redis 命令 Redis 命令用于在 redis 服务上执行操作. 要在 redis 服务上执行命令需要一个 redis 客户端.Redis 客户端在我们之前下载的的 redis 的安装包中. 语 ...
- 用vue.js学习es6(六):Iterator和for...of循环
一.Iterator (遍历器)的概念: 遍历器(Iterator)就是这样一种机制.它是一种接口,为各种不同的数据结构提供统一的访问机制.任何数据结构只 要部署Iterator接口,就可以完成遍历操 ...
- 使用视 meta 标签来控制手机浏览器布局
移动浏览器的Fennec一样呈现在一个虚拟的"窗口"页面(视),通常比屏幕宽.所以他们不需要去挤每个页面布局到一个小窗口(这会破坏许多非移动优化的网站) .用户可以平移和缩放才能看 ...
- BeautifulSoup :功能使用
# -*- coding: utf-8 -*- ''' # Author : Solomon Xie # Usage : 测试BeautifulSoup一些用法及容易出bug的地方 # Envirom ...
- theano scan optimization
selected from Theano Doc Optimizing Scan performance Minimizing Scan Usage performan as much of the ...
- DOM(文档对象模型)
1.定义: DOM是Document Object Model文档对象模型的缩写.是针对HTML和XML文档的一个API,通过DOM可以去改变文档. 例如:我们有一段HTML,那么如何访问第二层第一个 ...
- Oracle数据库to_date()和to_char()的相关
select * from T_A a where a.begintime=to_date('2013-1-1','yyyy-mm-dd');和select * from T_A a where to ...