Solidity数组

一.固定长度的数组（Arrays）

1.固定长度类型数组的声明

pragma solidity ^0.4.4;
 
contract C {
 
    // 数组的长度为5，数组里面的存储的值的类型为uint类型
    uint [5] T = [1,2,3,4,5];
}

2.通过length方法获取数组长度遍历数组求总和

pragma solidity ^0.4.4;
 
contract C {
 
    // 数组的长度为5，数组里面的存储的值的类型为uint类型
    uint [5] T = [1,2,3,4,5];
 
    // 通过for循环计算数组内部的值的总和
    function numbers() constant public returns (uint) {
        uint num = 0;
        for(uint i = 0; i < T.length; i++) {
            num = num + T[i];
        }
        return num;
    }
}

3.尝试修改T数组的长度

pragma solidity ^0.4.4;
 
contract C {
 
    uint [5] T = [1,2,3,4,5];
 
    function setTLength(uint len) public {
 
        T.length = len;
    }
}

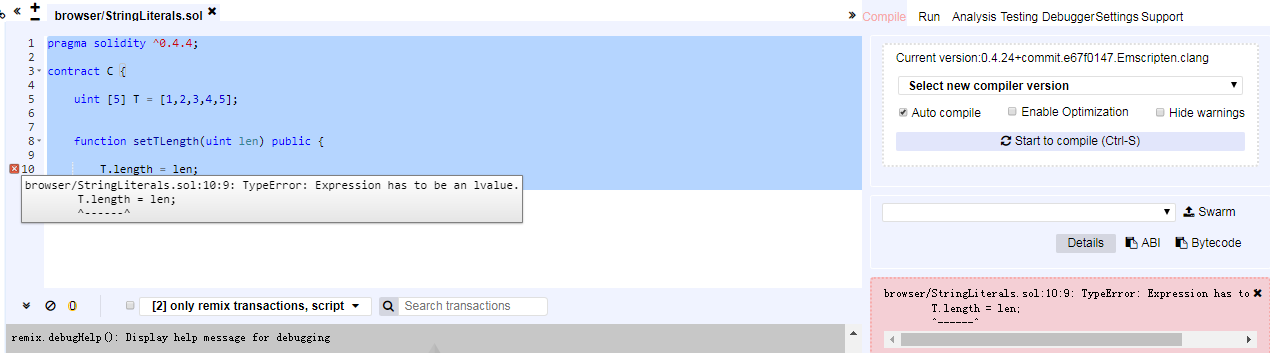
　　PS:声明数组时，一旦长度固定，将不能再修改数组的长度。

 4.尝试修改T数组内部值

pragma solidity ^0.4.4;
 
contract C {
 
    uint [5] T = [1,2,3,4,5];
 
    function setTIndex0Value() public {
 
        T[0] = 10;
    }
 
    // 通过for循环计算数组内部的值的总和
    function numbers() constant public returns (uint) {
        uint num = 0;
        for(uint i = 0; i < T.length; i++) {
            num = num + T[i];
        }
        return num;
    }
}

　　T数组初始的内容为[1,2,3,4,5]，总和为15 ，当我点击setTIndex0Value方法将第0个索引的1修改为10时，总和为24。

　　PS：通过一个简单的试验可证明固定长度的数组只是不可修改它的长度，不过可以修改它内部的值，而bytes0 ~ bytes32固定大小字节数组中，大小固定，内容固定，长度和字节均不可修改。

5.尝试通过push往T数组中添加值

pragma solidity ^0.4.4;
 
contract C {
    uint [5] T = [1,2,3,4,5];
 
    function pushUintToT() public {
 
        T.push(6);
    }
}

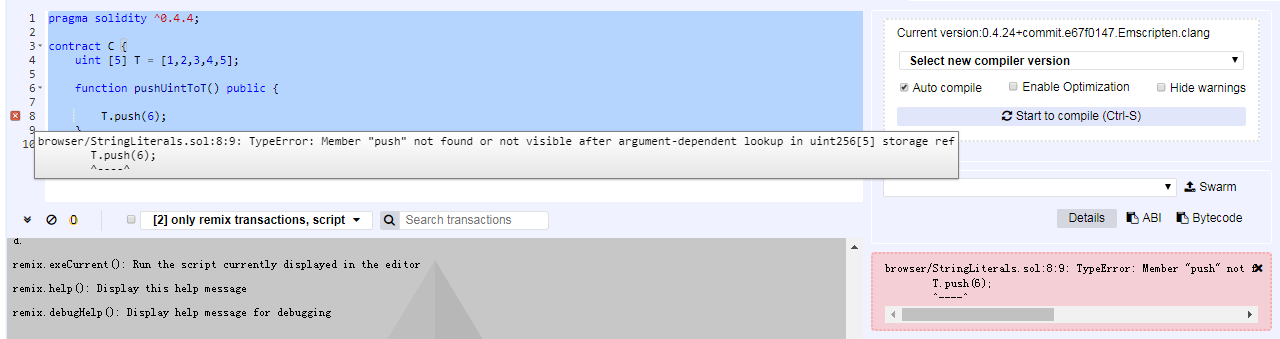
　　PS：固定大小的数组不能调用push方法向里面添加存储内容，声明一个固定长度的数组，比如：uint [5] T，数组里面的默认值为[0,0,0,0,0]，我们可以通过索引修改里面的值，但是不可修改数组长度以及不可通过push添加存储内容。

二.可变长度的Arrays

1.可变长度类型数组的声明

pragma solidity ^0.4.4;
 
contract C {
 
    uint [] T = [1,2,3,4,5];
 
    function T_Length() constant returns (uint) {
 
        return T.length;
    }
}

　　uint [] T = [1,2,3,4,5]，这句代码表示声明了一个可变长度的T数组，因为我们给它初始化了5个无符号整数，所以它的长度默认为5。

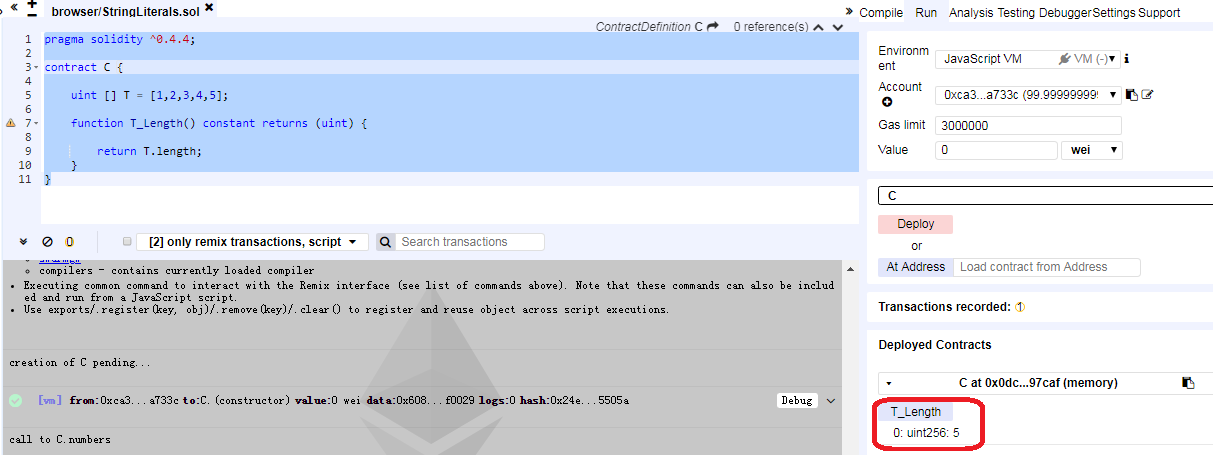
2.通过length方法获取数组长度遍历数组求总和

pragma solidity ^0.4.4;
 
contract C {
 
    uint [] T = [1,2,3,4,5];
 
    // 通过for循环计算数组内部的值的总和
    function numbers() constant public returns (uint) {
        uint num = 0;
        for(uint i = 0; i < T.length; i++) {
            num = num + T[i];
        }
        return num;
    }
}

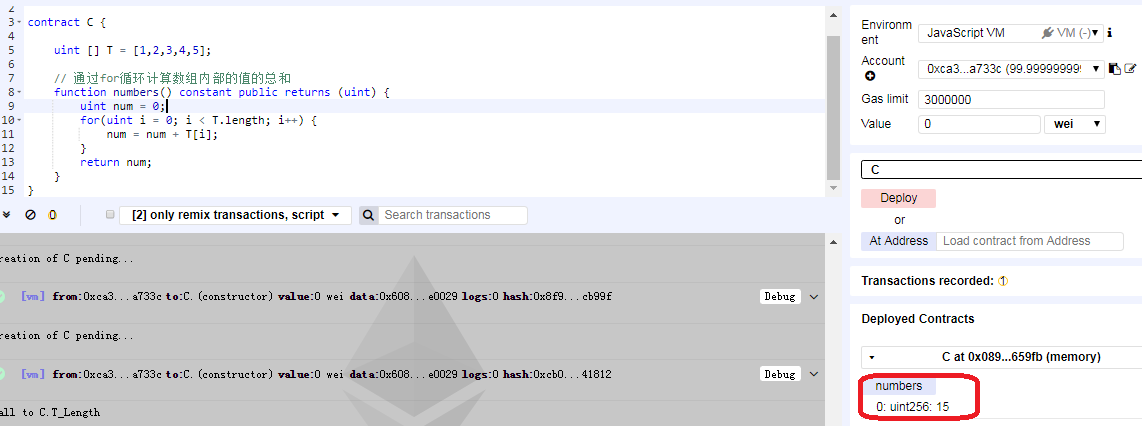
　　通过length方法获取数组长度遍历数组求总和

3.尝试修改T数组的长度

pragma solidity ^0.4.4;
 
contract C {
 
    uint [] T = [1,2,3,4,5];
 
    function setTLength(uint len) public {
 
        T.length = len;
    }
 
    function TLength() constant returns (uint) {
 
        return T.length;
    }
}

　　PS：对可变长度的数组而言，可随时通过length修改它的长度。

4.尝试通过push往T数组中添加值

pragma solidity ^0.4.4;
 
contract C {
 
    uint [] T = [1,2,3,4,5];
 
    function T_Length() constant public returns (uint) {
 
        return T.length;
    }
 
    function pushUintToT() public {
 
        T.push(6);
    }
 
    function numbers() constant public returns (uint) {
        uint num = 0;
        for(uint i = 0; i < T.length; i++) {
            num = num + T[i];
        }
        return num;
    }
}

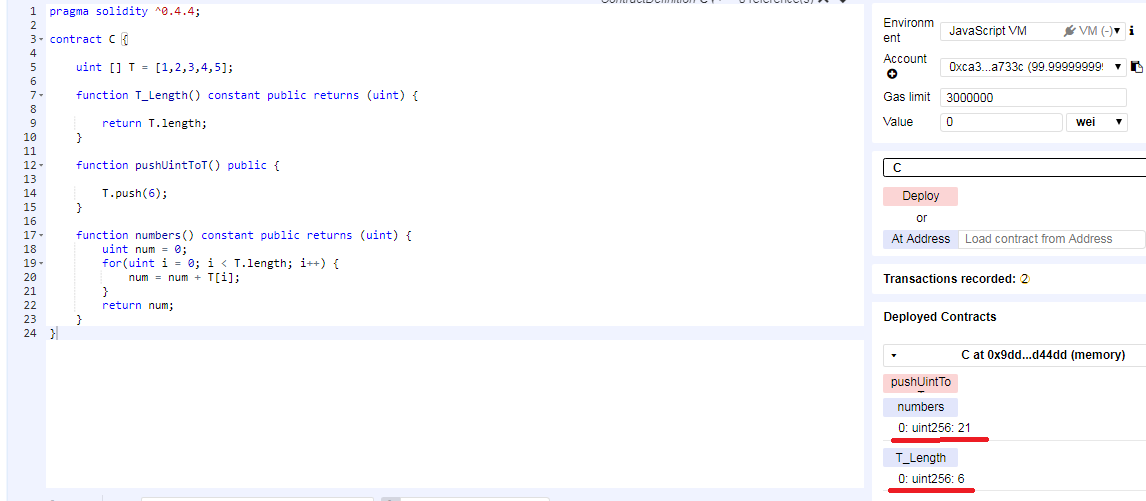
　　PS：当往里面增加一个值，数组的个数就会加1，当求和时也会将新增的数字加起来。

三.二维数组 - 数组里面放数组

pragma solidity ^0.4.4;
 
contract C {
 
    uint [2][3] T = [[1,2],[3,4],[5,6]];
 
    function T_len() constant public returns (uint) {
 
        return T.length; //
    }
}

　　uint [2][3] T = [[1,2],[3,4],[5,6]]这是一个三行两列的数组，你会发现和Java、C语言等的其它语言中二位数组里面的列和行之间的顺序刚好相反。在其它语言中，上面的内容应该是这么存储uint [2][3] T = [[1,2,3],[4,5,6]]。

　　上面的数组T是storage类型的数组，对于storage类型的数组，数组里面可以存放任意类型的值（比如：其它数组，结构体，字典／映射等等）。对于memory类型的数组，如果它是一个public类型的函数的参数，那么它里面的内容不能是一个mapping(映射／字典)，并且它必须是一个ABI类型。

四.创建 Memory Arrays
　　创建一个长度为length的memory类型的数组可以通过new关键字来创建。memory数组一旦创建，它不可通过length修改其长度。

pragma solidity ^0.4.4;
 
contract C {
 
    function f(uint len) {
        uint[] memory a = new uint[](7);
        bytes memory b = new bytes(len);
        // 在这段代码中 a.length == 7 、b.length == len
        a[6] = 8;
    }
}

五.数组字面量 Array Literals / 内联数组 Inline Arrays

pragma solidity ^0.4.4;
 
contract C {
 
    function f() public {
        g([1, 2, 3]);
    }
 
    function g(uint[3] _data) public {
        // ...
    }
}

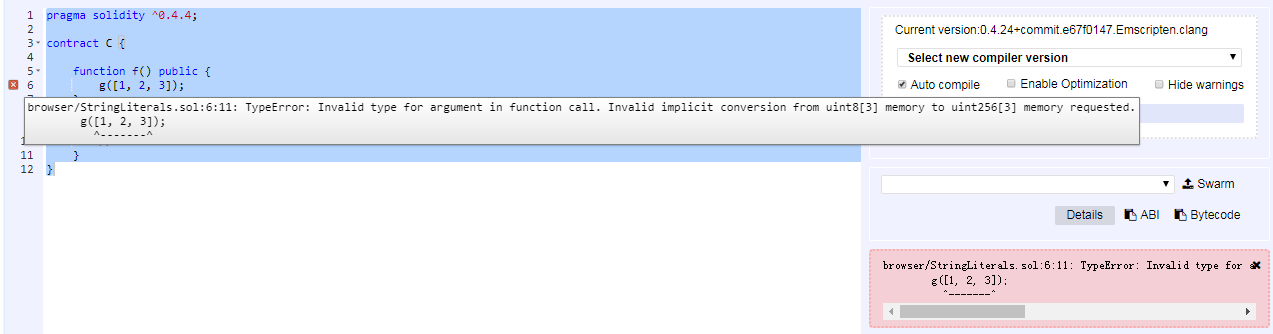
　　在上面的代码中，[1, 2, 3]是 uint8[3] memory 类型，因为1、2、3都是uint8类型，他们的个数为3，所以[1, 2, 3]是 uint8[3] memory 类型。但是在g函数中，参数类型为uint[3]类型，显然我们传入的数组类型不匹配，所以会报错。

　　正确的写法如下：

pragma solidity ^0.4.4;
 
contract C {
 
    function f() public {
        g([uint(1), 2, 3]);
    }
 
    function g(uint[3] _data) public {
        // ...
    }
}

　　在这段代码中，我们将[1, 2, 3]里面的第0个参数的类型强制转换为uint类型，所以整个[uint(1), 2, 3]的类型就匹配了g函数中的uint[3]类型。

memory类型的固定长度的数组不可直接赋值给storage/memory类型的可变数组

　　TypeError: Type uint256[3] memory is not implicitly convertible to expected type uint256[] memory.

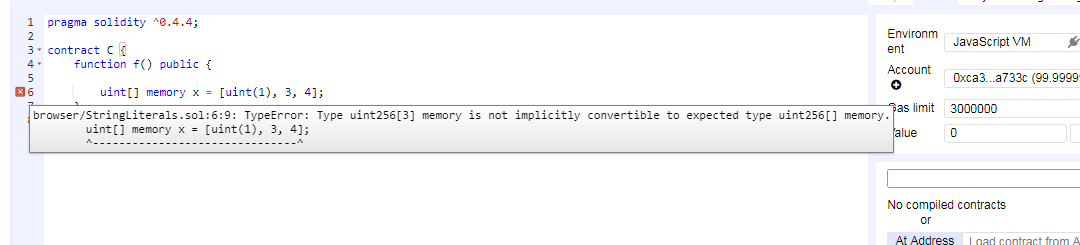
　　TypeError: Type uint256[3] memory is not implicitly convertible to expected type uint256[] storage pointer

　　正确使用

pragma solidity ^0.4.4;
 
contract C {
    function f() public {
 
        uint[3] memory x = [uint(1), 3, 4];
    }
}

六.创建固定大小字节数组／可变大小字节数组
　　之前我们的文章中深入讲解了bytes0 ~ bytes32、bytes以及string的使用。bytes0 ~ bytes32创建的是固定字节大小的字节数组，长度不可变，内容不可修改。而string是特殊的可变字节数组，它可以转换为bytes以通过length获取它的字节长度，亦可通过索引修改相对应的字节内容。

　　创建可变字节数组除了可以通过bytes b = new bytes(len)来创建外，我们亦可以通过byte[] b来进行声明。

　　而bytes0 ~ bytes32我们可以通过byte[len] b来创建，len 的范围为0 ~ 32。不过这两种方式创建的不可变字节数组有一小点区别，bytes0 ~ bytes32直接声明的不可变字节数组中，长度不可变，内容不可修改。而byte[len] b创建的字节数组中，长度不可变，但是内容可修改。

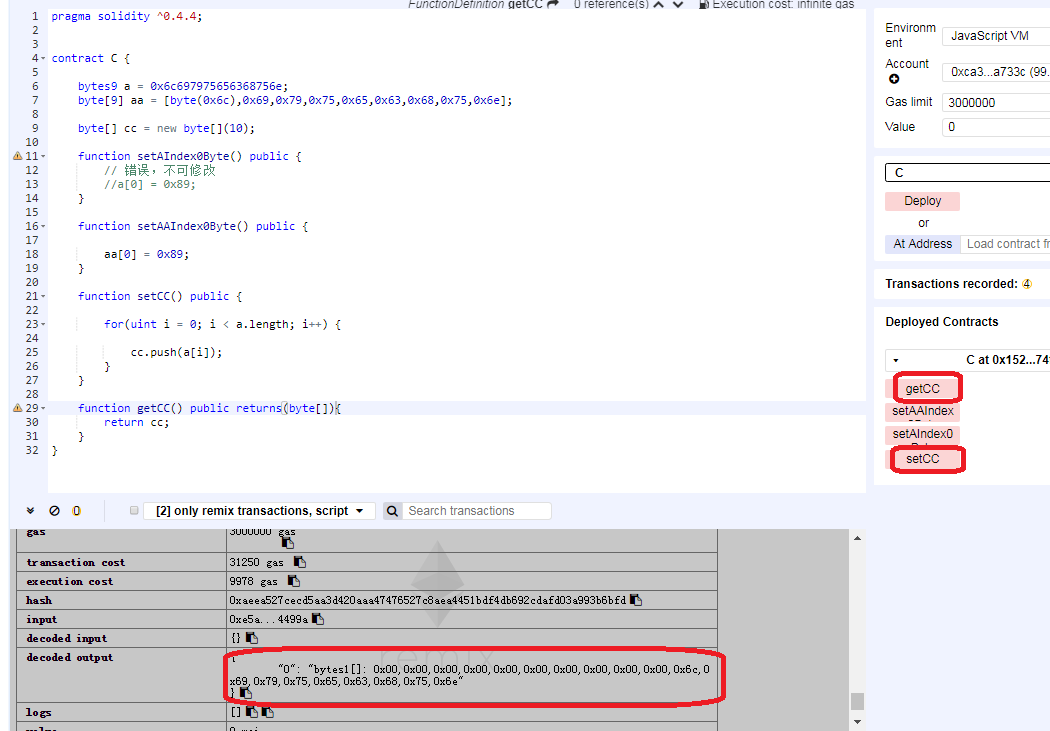
pragma solidity ^0.4.4;
 
contract C {
 
    bytes9 a = 0x6c697975656368756e;
    byte[9] aa = [byte(0x6c),0x69,0x79,0x75,0x65,0x63,0x68,0x75,0x6e];
 
    byte[] cc = new byte[](10);
 
    function setAIndex0Byte() public {
        // 错误，不可修改
        a[0] = 0x89;
    }
 
    function setAAIndex0Byte() public {
 
        aa[0] = 0x89;
    }
 
    function setCC() public {
 
        for(uint i = 0; i < a.length; i++) {
 
            cc.push(a[i]);
        }
    }
}

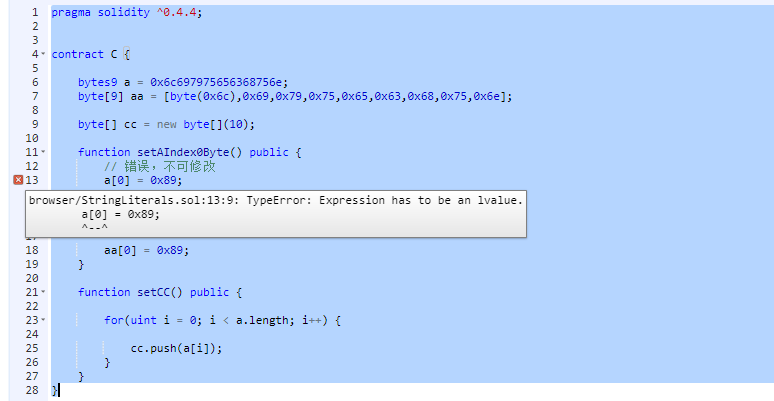
七.总结

　　本篇文章系统讲解了可变与不可变数组的创建、以及二位数组与其它语言中二位数组的区别，同时讲解了如何创建memory类型的数组以及对bytes0 ～ bytes32、bytes与byte[]对比分析。

文章来源：https://blog.csdn.net/liyuechun520/article/details/78410733