[Bayesian] “我是bayesian我怕谁”系列 - Boltzmann Distribution

使用Boltzmann distribution还是Gibbs distribution作为题目纠结了一阵子，选择前者可能只是因为听起来“高大上”一些。本章将会聊一些关于信息、能量这方面的东西，体会“交叉学科”的魅力。

In statistical mechanics and mathematics, a Boltzmann distribution (also called Gibbs distribution) is a probability distribution, probability measure, or frequency distribution of particles in a system over various possible states.

Hi 菜鸡，

神经网络的Boltzmann Machine；

期望传播中提及的Ising model；

强化学习中涉及的训练收敛问题；

够了么？问问自己有没有必要了解？

本系列文章乃自娱自乐，防止衰老；只“雪中送炭”，不提供”全套服务“。

---

• Softmax与分子运动学

一个用于描述稳态系统的内部粒子状态的分布：

任何（宏观）物理系统的温度都是组成该系统的分子和原子的运动的结果。

对于大量粒子来说，处于一个特定的速度范围的粒子所占的比例却几乎不变，如果系统处于或接近处于平衡。---- 分布的期望是”稳定的“，是不是这么个感觉

麦克斯韦-玻尔兹曼分布具体说明了这个比例。

既然是个分布，概率密度函数的样子是：

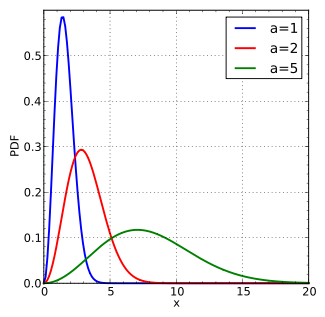
百度百科：click me

写到这里，内心是湿润的，远古时期的物理奥赛底子竟然到今天还发挥着余热，啊哈哈哈哈哈……

麦斯威尔- 玻尔兹曼统计量给出了在某些假设条件下给定单粒子微观状态中发现的平均粒子数：

 

 

i和j是单粒子微态的指标（或标签）
　　N_i是单粒子微观状态i中的平均粒子数，
　　N是系统中的粒子总数，
　　E_i是microstate i的能量，
　　T是系统的平衡温度，
　　k是波尔兹曼常数。

再瞧：Softmax回归

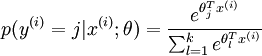
可能你只是看到了”e族函数处处可导“的性质，想到了”归一化“这样的概念，但在另一个层次，有人可能会这样理解：

“神经网络Softmax的公式形式是分子运动学的热能公式的变种，output对应了能量输出，分类的物理意义对应的就是不同能量层级的分子的个数比，也就是成为某类的概率比。如此看来，NN的各个权值的意义，原来就是能量值。NN的收敛，就是能量的分配，系统entropy最大的过程。”

这，又是一个如同pca章节讲述的故事，是否点醒了菜鸡。

• Cross Entropy与KL Divergence

Cross Entropy是求loss的一种方式，对于菜鸡起初难以理解，毕竟另一个“最小二乘”的loss计算方式理解起来会简单的多。

表面美，不一定内在美。

Cross Entropy的依据显然是信息论。

(1) X=x时的Entropy :

(2) 变量X的Entropy (the average amount of information) : 

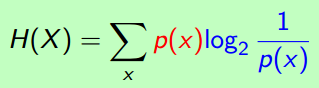
形式好看了些。

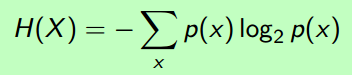
(3) 举个栗子

0-1离散分布，0的概率是θ，１的概率是(1 − θ)，那么：

H(X) = −θ log θ − (1 − θ) log(1 − θ)

可见，当θ=0.5时，这样的变量X才拥有最大H。

基础概念过后，有请Cross Entropy的姐姐Relative Entropy：

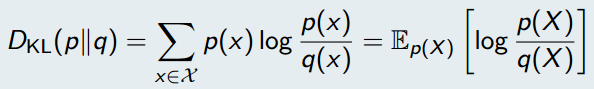
原来Relative Entropy就是Kullback-Leibler (KL) divergence。

举个栗子：两个参数不同的0-1分布的度量，如下：

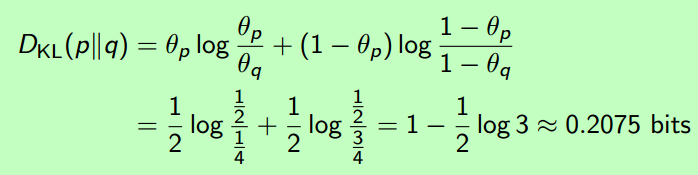
(4) 那么，Cross Entropy又是什么？

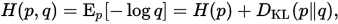
可以看出，交叉熵与相对熵仅相差了H(p)

当p已知时，可以把H(p)看做一个常数，此时交叉熵与KL距离在行为上是等价的，都反映了分布p，q的相似程度。

也就是说，收敛的过程就是逐渐接近ground truth分布的过程。

• Entropy与Mutual Information

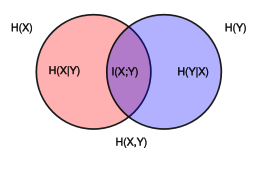
From: http://www.ece.tufts.edu/ee/194NIT/lect01.pdf

The mutual information between two discreet random variables X, Y jointly distributed according to p(x, y) is given by :

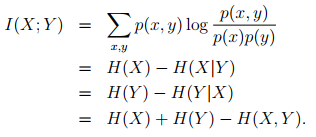
表示两个变量之间的依赖关系。

知道这个东西做什么？一点浅显的见解：能量是一种宏观的体现，信息往往也是如此，如何度量是个问题，这至少给你提供了一套度量方法。

• Hopfield Nets与非线性动力学

主要是看中了其中所涉及的能量公式，一起来个赏析。

信息存储的原理、例子见此链接：https://wenku.baidu.com/view/ef6e6fbec77da26925c5b0af.html

有点马尔科夫迭代收敛到稳态的感觉。

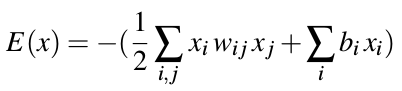
网络的稳定性度量。

为何将能量函数定义为如此形式？如下解答，一种“仿生学”。

• Boltzmann Machine与模拟退火

Ref：最通俗的方法解释退火算法

这里有一个Bolzmann常数。

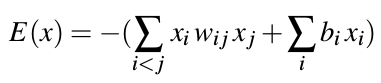
能量的变化作为什么角色？

可见，求的是：O_i = 1的概率，也就是P_a的概率。

Therefore, if all other components are fixed, the probability of x_i taking the value 1 or 0 must be：

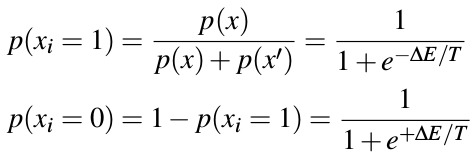
In other words, there is some probability of moving to a higher energy state (or remaining in a higher energy state even when a lower one is available).

可见，具备了模拟退火的feature，为了防止局部极小值，也可能以一定的概率走一奇招！这个概率就与当前的能量大小有关！

Restricted Boltzmann Machine 

The aim is that the hidden units should learn some hidden features or “latent variables” which help the system to model the distribution of the inputs.

Two-layer bi-directional neural network，新的能量公式：

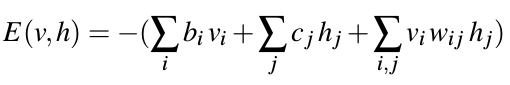
关于训练的具体细节，可参见：http://www.cnblogs.com/neopenx/p/4399336.html

但下图所示，训练的基本过程，Gibbs sampling。

到这里，便终于揭示出本文开头提及的一个真相：Boltzmann为何与Gibbs有了关系。

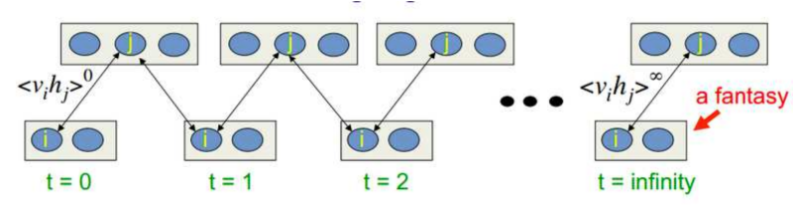
关于能量，总结套路于此：

”由能量决定概率分布，根据概率分布随机变换神经元的状态，直到收敛，整个网络达到稳定状态。“

读完此文，也希望你对神经网络有新的认识。