自适应滤波：最小均方误差滤波器（LMS、NLMS）

作者：桂。

时间：2017-04-02  08:08:31

链接：http://www.cnblogs.com/xingshansi/p/6658203.html

声明：欢迎被转载，不过记得注明出处哦~

---

【读书笔记08】

前言

西蒙.赫金的《自适应滤波器原理》第四版第五、六章：最小均方自适应滤波器（LMS，Least Mean Square）以及归一化最小均方自适应滤波器（NLMS，Normalized Least Mean Square）。全文包括：

　　1）LMS与维纳滤波器（Wiener Filter）的区别；

　　2）LMS原理及推导；

　　3）NLMS推导；

　　4）应用实例；

内容为自己的读书记录，其中错误之处，还请各位帮忙指出！

一、LMS与维纳滤波器（Wiener Filter）的区别

• 这里介绍的LMS/NLMS，通常逐点处理，对应思路是：随机梯度下降；
• 对于Wiener Filter，给定准则函数J，随机/批量梯度都可以得出最优解；
• LMS虽然基于梯度下降，但准则仅仅是统计意义且通常引入误差，可以定义为$J_0$，简而言之$J$通常不等于$J_0$，得出的最优解$w_o$自然也通常不等于维纳最优解；
• 分析LMS通常会分析稳定性，稳定性是基于Wiener解，之前已给出分析。但LMS是Wiener解的近似，所以：迭代步长的稳定性，严格适用于Wiener解，对于LMS只是一种近似参考，并没有充分的理论依据。

下文的分析仍然随机梯度下降的思路进行。

二、LMS原理及推导

LMS是时间换空间的应用，如果迭代步长过大，仍然有不收敛的问题；如果迭代步长过小，对于不平稳信号，还没有实现寻优就又引入了新的误差，屋漏偏逢连夜雨！所以LMS系统是脆弱的，信号尽量平稳、哪怕短时平稳也凑合呢。

给出框图：

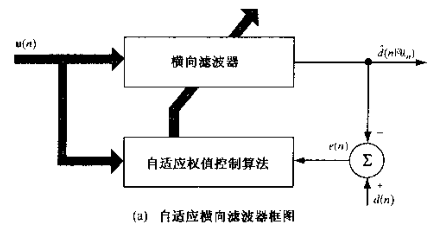
关于随机梯度下降，可以参考之前的文章。这里直接给出定义式：

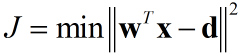
利用梯度下降：

$- \nabla J = {\bf{x}}{\left( {{{\bf{w}}^T}{\bf{x}} - {d}} \right)^T}$

给出LMS算法步骤：

1）给定$\bf{w}(0)$，且$1<\mu<1/\lambda_{max}$；

2）计算输出值：$y\left( k \right) = {\bf{w}}{\left( k \right)^T}{\bf{x}}\left( k \right)$;

3）计算估计误差：$e\left( k \right) = d\left( k \right) - y\left( k \right)$;

4）权重更新：${\bf{w}}\left( {k + 1} \right) = {\bf{w}}\left( k \right) + \mu e\left( k \right){\bf{x}}\left( k \right)$

三、NLMS推导

看到Normalized，与之联系的通常是约束条件，看到约束不免想起拉格朗日乘子。思路有了，现在开始分析：

假设${\bf{w}}\left( k \right) \Rightarrow {\bf{w}}\left( {k + 1} \right)$得到最优权重，即：

$d\left( k \right) = {\bf{w}}\left( {k + 1} \right){\bf{x}}\left( k \right)$

我们希望在得到期望权重的附近，迭代不要过大以免错过最优值：

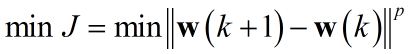
写出准则函数：

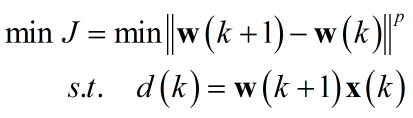
利用之前文章提到的拉格朗日乘子法：

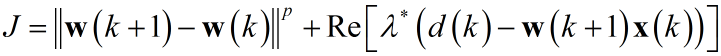
这里仅仅分析基于欧式距离$p = 2$的情形，其它范数类似。求解得出:

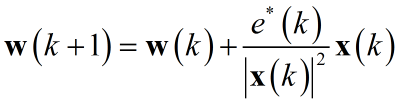
通常为了防止分母为零迭代方程需要修正，而修正后步长存在偏差，故添加调节因子$\mu$：

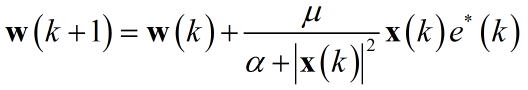
给出NLMS算法步骤：

1）给定$\bf{w}(0)$；

2）计算输出值：$y\left( k \right) = {\bf{w}}{\left( k \right)^T}{\bf{x}}\left( k \right)$;

3）计算估计误差：$e\left( k \right) = d\left( k \right) - y\left( k \right)$;

4）权重更新：${\bf{w}}\left( {k + 1} \right) = {\bf{w}}\left( k \right) + \frac{\mu }{{\alpha  + {{\left| {{\bf{x}}\left( k \right)} \right|}^2}}}{\bf{x}}\left( k \right){e^*}\left( k \right)$

四、应用实例

　　A-自适应噪声滤波

这个场景可以简化为：一个房间两个麦克风，一个放在远处采集房间噪声，一个放在说话人附近采集带噪语音，认为两个音频文件的噪声相似。

这里噪声直接用白噪声，对应实际场景可以认为是采集的噪声数据，给出主要代码：

[s, fs, bits] = wavread(filename);
s=s-mean(s);
s=s/max(abs(s));
N=length(s);
time=(0:N-1)/fs;
%%生成带噪信号
clean=s';
ref_noise=0.1*randn(1,length(s));
mixed = clean+ref_noise
%NLMS
mu=0.05;M=32;espon=1e-4;
% [en,wn,yn]=lmsFunc(mu,M,ref_noise,mixed);%
[en,wn,yn]=nlmsFunc(mu,M,ref_noise,mixed,espon);

LMS代码：

function [e,w,ee]=lmsFunc(mu,M,u,d)
% Normalized LMS
% Call:
% [e,w]=nlms(mu,M,u,d,a);
%
% Input arguments:
% mu = step size, dim 1x1
% M = filter length, dim 1x1
% u = input signal, dim Nx1
% d = desired signal, dim Nx1
% a = constant, dim 1x1
%
% Output arguments:
% e = estimation error, dim Nx1
% w = final filter coefficients, dim Mx1
%intial value 0

w=zeros(M,1); %This is a vertical column

%input signal length
N=length(u);
%make sure that u and d are colon vectors
u=u(:);
d=d(:);
%NLMS
ee=zeros(1,N);
for n=M:N %Start at M (Filter Length) and Loop to N (Length of Sample)
    uvec=u(n:-1:n-M+1); %Array, start at n, decrement to n-m+1
    e(n)=d(n)-w'*uvec;
    w=w+2*mu*uvec*e(n);
    % y(n) = w'*uvec; %In ALE, this will be the narrowband noise.
end

NLMS代码：

function [e,w,ee]=nlmsFunc(mu,M,u,d,a)
% Normalized LMS
% Call:
% [e,w]=nlms(mu,M,u,d,a);
%
% Input arguments:
% mu = step size, dim 1x1
% M = filter length, dim 1x1
% u = input signal, dim Nx1
% d = desired signal, dim Nx1
% a = constant, dim 1x1
%
% Output arguments:
% e = estimation error, dim Nx1
% w = final filter coefficients, dim Mx1
%intial value 0

w=zeros(M,1); %This is a vertical column

%input signal length
N=length(u);
%make sure that u and d are colon vectors
u=u(:);
d=d(:);
%NLMS
ee=zeros(1,N);
for n=M:N %Start at M (Filter Length) and Loop to N (Length of Sample)
    uvec=u(n:-1:n-M+1); %Array, start at n, decrement to n-m+1
    e(n)=d(n)-w'*uvec;
    w=w+mu/(a+uvec'*uvec)*uvec*e(n);
    % y(n) = w'*uvec; %In ALE, this will be the narrowband noise.
end

对应结果图：

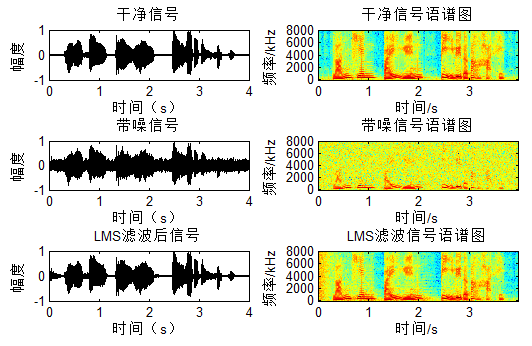
可以看出LMS/NLMS在最开始都有一个自适应的过程。

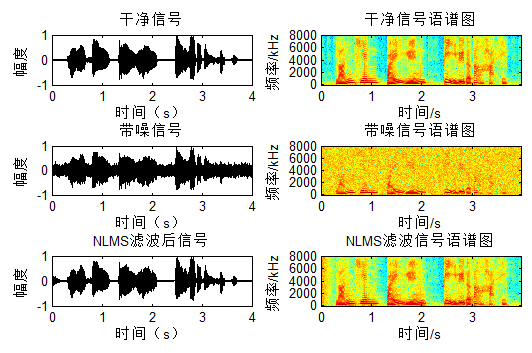
NLMS基于信号$x$的能量实现变步长，信号大步长小，信号小则步长大：目标信号明显，则迭代细致，不明显，则一带而过，呵呵，跟平时看书还挺像，聪明的孩子。

再来看一组信号：

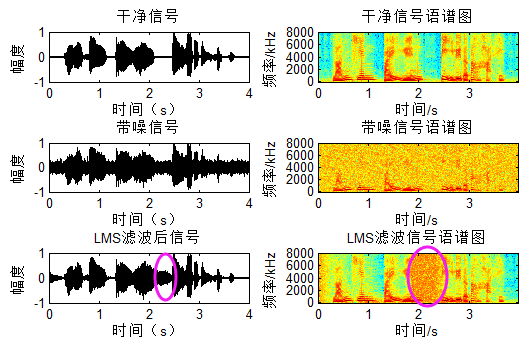
这里在中间令噪声突变，可以看到滤波器又需要重新自适应，因此对于短时平稳LMS勉强使用，如果不断变呢？非平稳LMS自然无效了，这个时候就需要Kalman Filter来搭把手。

　　B-工频噪声滤波

现在有一个音频信号，分析频谱：

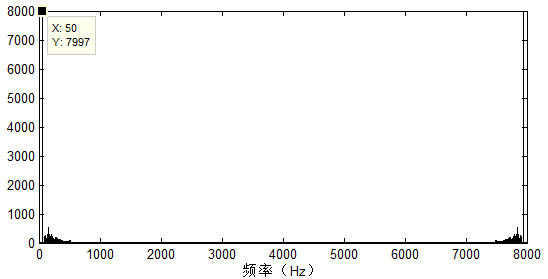
可以看到信号带有明显的$50Hz$噪声，我们知道$50Hz$的正弦与余弦可以组合成任意相位的$50Hz$频率信号，基于这个思路，进行自适应滤波：

给出主要的代码：

x1=cos(2*pi*50*time);
x2=sin(2*pi*50*time);
w1=0.1;
w2=0.1;
e=zeros(1, N);
y=zeros(1, N);
mu=0.05;
for i=1: N
  y(i)=w1 * x1(i)+ w2 * x2(i);
  e(i) =x(i)-y(i);
  w1=w1+mu * e(i) * x1(i);
  w2=w2+mu * e(i) * x2(i);
end

结果图可以看出，工频50Hz滤除：

基于LMS的应用还有很多，不一一说啦。

参考：

• Simon Haykin 《Adaptive Filter Theory Fourth Edition》.
• 宋知用：《MATLAB在语音信号分析和合成中的应用》.