线搜索(line search)方法

在机器学习中, 通常需要求某个函数的最值(比如最大似然中需要求的似然的最大值). 线搜索(line search)是求得一个函数\(f(x)\)的最值的两种常用迭代方法之一(另外一个是trust region). 其思想是首先求得一个下降方向,在这个方向上\(f(x)\)会下降, 然后是求得\(f(x)\)在这个方向上下降的步长. 求下降方向的方法有很多, 比如梯度下降, 牛顿方法和Quasi-Newton方法, 而步长可以是固定值, 也可以通过诸如回溯线搜索来求得.

1. 线搜索(line search)

线搜索是一种迭代的求得某个函数的最值的方法. 对于每次迭代, 线搜索会计算得到搜索的方向\(p_k\)以及沿这个方向移动的步长\(\alpha_k\).

大多数的线搜索方法都会要求\(p_k\)是下降方向(descent direction), 亦即需要满足以下条件: \({p_k}^T{\nabla}f_k <0\), 这样就能够保证函数\(f\)(x)沿着这个方向是下降的. 一般来说, 搜索方向是\(p_k=-B_k^{-1}\nabla f_k\)

其中\(B_k\)是一个对称非奇异矩阵. 在最深下降(steepest descent)方法中, \(B_k\)是单位矩阵\(I\), 在牛顿方法(Newton)中\(B_k\)则是海森(Hessian)矩阵\({\nabla}^2f(x_k)\), 在Quasi-Newton方法中通过迭代求得Hessian矩阵的近似矩阵.

当\(p_k\)由上式定义, 且\(B_k\)是正定矩阵时: $$p_k^T\nabla f_k = -\nabla f_k^T B_k^{-1}\nabla f_k <0$$所以\(p_k\)是下降方向(descent direction).

2. 步长

步长\(\alpha\)应该最小化下面的函数:$$\phi (\alpha)=f(x_k+\alpha p_k)$$

但是求得使上式最小的\(\alpha\)比较困难, 且计算量比较大, 实际常用的方法是在可接受的计算量的情况下尽可能的求得较大的步长, 以使得\(\phi(\alpha)\)尽可能的降低. 经典的线搜索方法通过迭代来求得\(\alpha\), 直至达到某个停止条件. 一般的线搜索方法都包含以下两个步骤:

1. bracketing: 求得一个包含理想的步长的区间
2. 二分法或者插值法: 在这个区间内使用二分法或者插值法来求得步长

2.1 对于凸函数的二分搜索算法

如果\(f(x)\)是一个可微分的凸函数, 则我们的目标是求得\(\alpha\), 使得$$\alpha=arg \min_{\lambda>0}f(x+\lambda p)$$

令\(\phi (\alpha)=f(x_k+\alpha p_k)\), 其中\(\phi(\alpha)\)是\(\alpha\)的凸函数, 所以问题转化为求:$$\bar{\alpha}=arg \min_{\alpha>0} \phi(\alpha)$$

因为\(\phi(\alpha)\)是凸函数, 所以\(\phi'(\bar{\alpha})=0\). 可以得到\(\phi'(\alpha)=\nabla f(x+\alpha p)^T p\), 因为p是梯度下降方向, 所以\(\phi'(0)<0\).

假设我们知道一个\(\hat{\alpha}\)使得\(\phi'(\hat{\alpha})>0\), 那么使得\(\phi'(\bar{\alpha})=0\)的\(\alpha\)肯定位于(0,\(\hat{\alpha}\))区间内. 然后我们可以使用以下二分查找算法来求解\(\phi'(\alpha) \approx 0\)

1. 令k=0, \(\alpha_l :=0\), \(\alpha_u :=\hat{\alpha}\)

令\(\tilde{\alpha}=\frac{\alpha_u + \alpha_l}{2}\), 然后计算\(\phi'(\tilde{\alpha})\):

• 如果\(\phi'(\tilde{\alpha})>0\), 则令\(\alpha_u :=\tilde{\alpha}\), 令\(k\gets k+1\)
• 如果\(\phi'(\tilde{\alpha})<0\), 则令\(\alpha_l :=\tilde{\alpha}\), 令\(k\gets k+1\)
• 如果\(\phi'(\tilde{\alpha})=0\), 停止迭代

2.2 回溯线搜索(backtracking line search)

使用二分查找法来求步长的计算复杂度很高, 因为在最小化\(f(x)\)的每次迭代中我们都需要执行一次线搜索, 而每次线搜索都要用上述的二分查找算法. 我们可以在牺牲一定的精度的条件下来加快计算速度, 回溯线搜索是一种近似线搜索算法.

首先, 我们要求每次的步长\(\alpha_k\)都使得\(f(x)\)充分的降低:$$f(x_k +\alpha p_k)\leq f(x_k)+c_1 \alpha \nabla f_k^T p_k$$

上述条件称作充分下降条件, 其中\(c_1 \in (0,1)\), 一般来说\(c_1=10^{-4}\). 亦即\(f(x)\)的下降应该至少和\(\alpha_k\)以及\(\nabla f_k^T p_k\)成正比. 如下图所示, 上式的右边\(f(x_k)+c_1 \alpha \nabla f_k^T p_k\)是一个线性函数, 可以表示为\(l(\alpha)\).

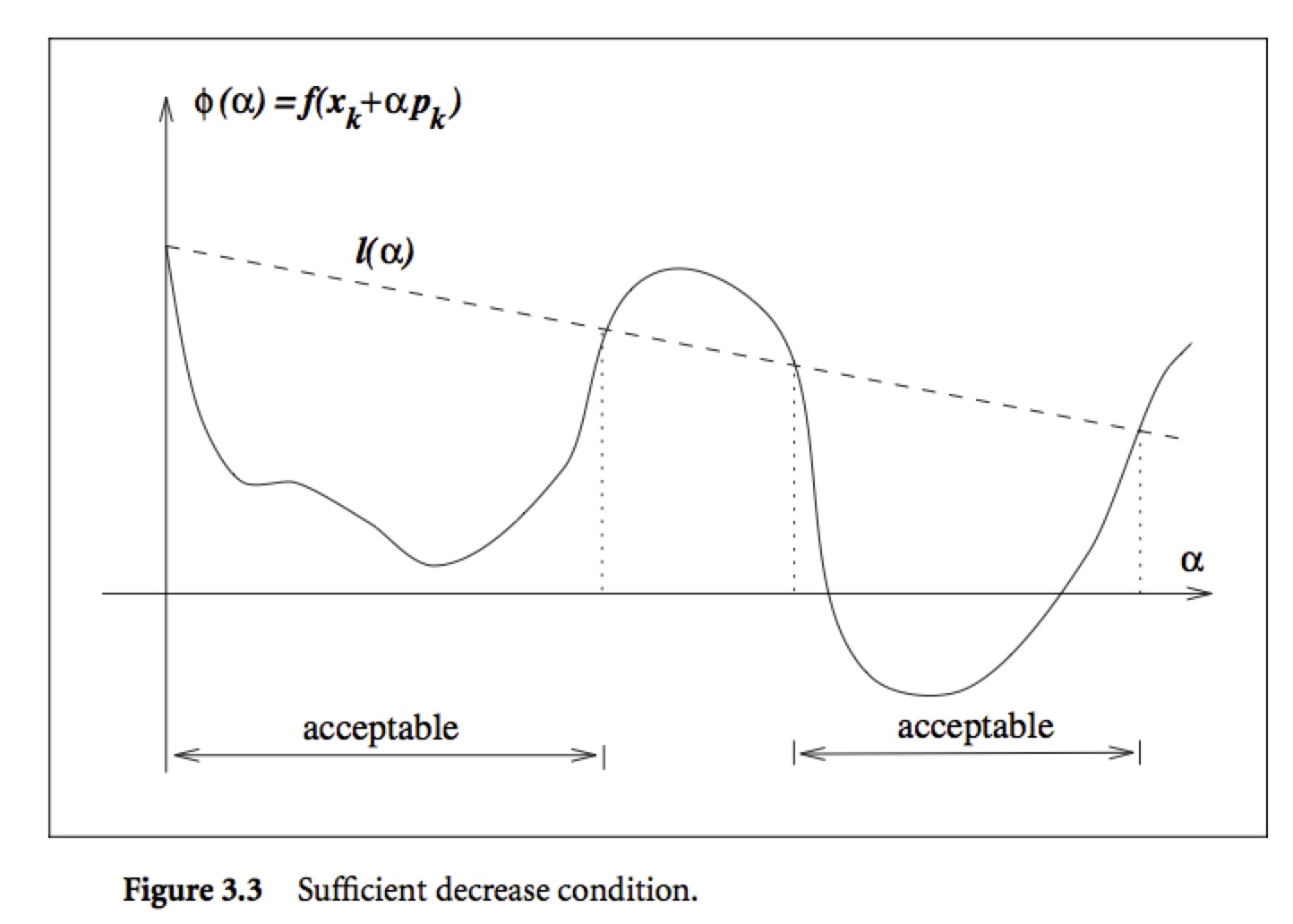
充分下降条件规定只有使得\(\phi(\alpha)\leq l(\alpha)\)的\(\alpha\)才满足条件. 其区间如上图所示.

单独只有充分下降条件是不够的, 因为如上图, 所有充分小的\(\alpha\)都满足上述条件, 但是\(\alpha\)太小会导致下降不充分, 为了排除这些小的\(\alpha\), 我们引入了第二个要求, 亦即曲率条件(curvature condition):$$\nabla f(x_k + \alpha_k p_k)^T p_k \geq c_2 \nabla f_k^T p_k$$其中\(c_2 \in (c_1,1)\). 上式的左边就是\(\phi'(\alpha_k)\), 右边则是\(\phi'(0)\), 亦即上式要求\(\phi'(\alpha_k)\)大于等于\(c_2\)倍的\(\phi'(0)\), 这是因为如果\(\phi'(\alpha)\)是很小的负数, 则我们可以在这个方向上继续使得\(f(x)\)下降更多. 如下图所示

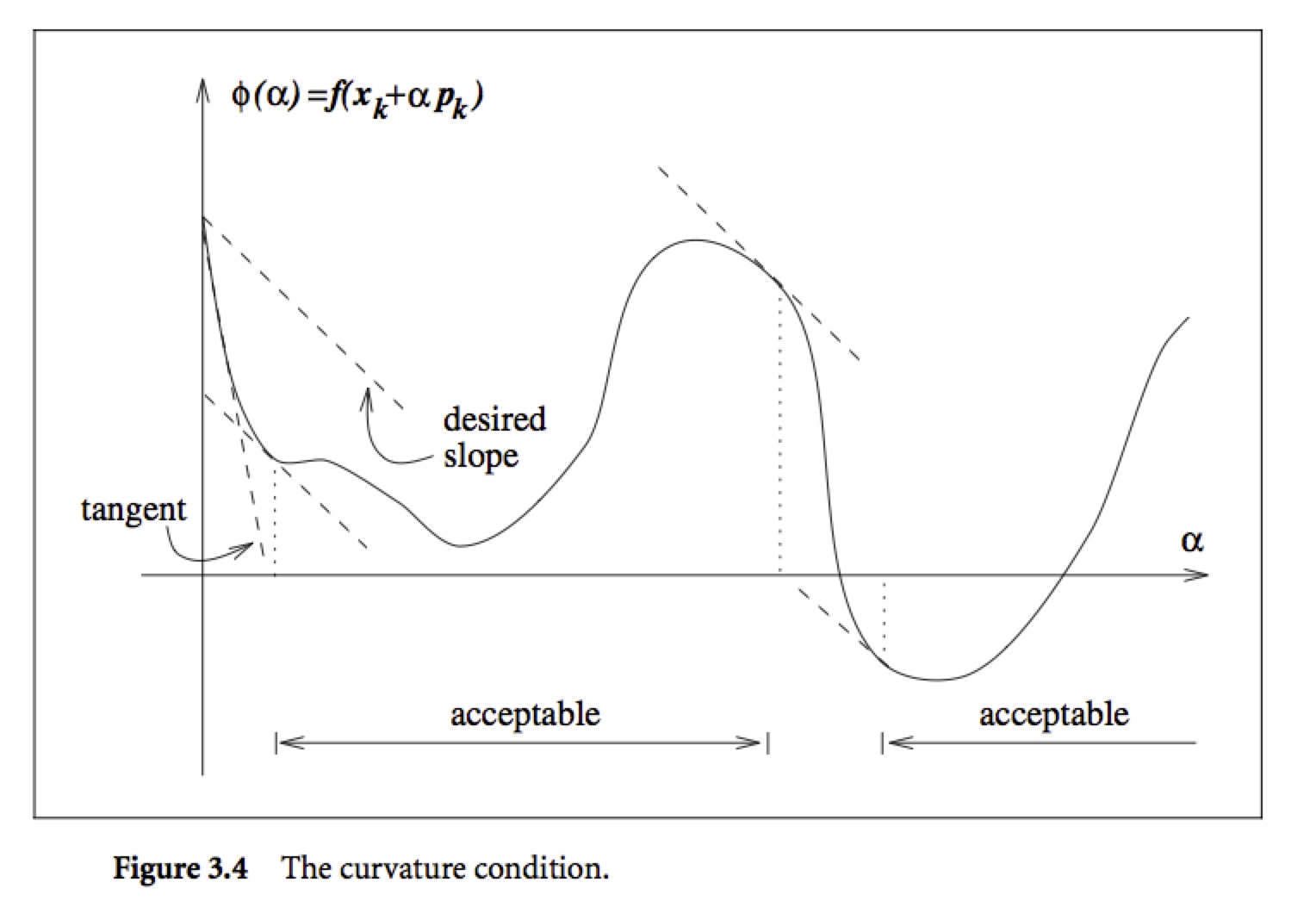
上述两个条件合起来称作Wolfe条件:

$$f(x_k +\alpha p_k)\leq f(x_k)+c_1 \alpha \nabla f_k^T p_k$$

$$\nabla f(x_k + \alpha_k p_k)^T p_k \geq c_2 \nabla f_k^T p_k$$

其中\(0<c_1 < c_2 <1\)

我们可以使用以下算法来求得满足Wolfe条件的步长\(\alpha\), 其主要思想是从一个初始的步长之后逐步减少\(\alpha\), 直至其满足充分下降条件, 同时可以防止\(\alpha\)变得太小:

1. 选择一个\(\bar(\alpha)>0, \rho, c\in (0,1);\)令\(\alpha \gets \bar{\alpha}\)
2. 重复以下步骤直到\(f(x_k +\alpha p_k)\leq f(x_k)+c_1 \alpha \nabla f_k^T p_k\):

• \(\alpha \gets \rho \alpha\)

3.  返回\(\alpha_k=\alpha\)

参考文献:

[1]. Numerical Optimization, Chapter 3, p35-p42. J. Nocedal, S.Wright.

[2]. Continuous Optimization Methods: Line search methods: one-dimensional optimization.

[3]. Wikipedia: Line Search.