Luogu 1429 平面最近点对 | 平面分治

Luogu 1429 平面最近点对

题目描述

给定平面上n个点，找出其中的一对点的距离，使得在这n个点的所有点对中，该距离为所有点对中最小的

输入输出格式

输入格式：

第一行：n；2≤n≤200000

接下来n行：每行两个实数：x y，表示一个点的行坐标和列坐标，中间用一个空格隔开。

输出格式：

仅一行，一个实数，表示最短距离，精确到小数点后面4位。

这是一道平面上的分治。

这是一个平面，我们把它分成两半，使x坐标位于最中间的两个点分到左右两侧：

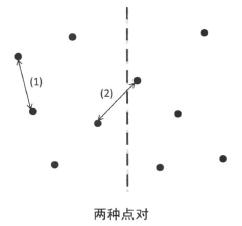
对于同在左侧或同在右侧的点对，我们可以递归处理；对于分别位于两侧的点对，如何处理呢？

设递归处理后我们知道同在左侧和同在右侧的点对中，最小距离是d；那么需要枚举的“分别位于两侧的点对”的两个端点的横坐标一定都位于中线左/右距离不超过d的范围内。

当枚举左侧的一个点的时候，右侧只需要找y坐标更小，且y坐标相差不超过d的点，与左侧的点配对。

有了以上两条限制，对于一个点p，另一侧需要与它配对的点不超过6个。

至于具体实现，要先把所有点按照x坐标排序，然后再递归的过程中按照y坐标排序。子区间内部点的顺序被修改（从按x排序变成按y排序），并不会影响母区间的划分，因为在递归进入子区间前母区间已经划分好了。

AC代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define space putchar(' ')
#define enter putchar('\n')
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
template <class T>
void read(T &x){
    char c;
    bool op = 0;
    while(c = getchar(), c < '0' || c > '9')
	if(c == '-') op = 1;
    x = c - '0';
    while(c = getchar(), c >= '0' && c <= '9')
	x = x * 10 + c - '0';
    if(op) x = -x;
}
template <class T>
void write(T x){
    if(x < 0) putchar('-'), x = -x;
    if(x >= 10) write(x / 10);
    putchar('0' + x % 10);
}

const int N = 200005;
int n;
struct point {
    double x, y;
    point operator - (const point &b){
	return (point){x - b.x, y - b.y};
    }
    double norm(){
	return sqrt(x * x + y * y);
    }
    bool operator < (const point &b) const{
	return x < b.x;
    }
} p[N], a[N], b[N], c[N];

double solve(int l, int r){
    if(l >= r) return 1e20;
    int mid = (l + r) >> 1;
    double xmid = (p[mid].x + p[mid + 1].x) / 2;
    double d = min(solve(l, mid), solve(mid + 1, r));
    int pos = l, pb = 0, pc = 0, pl = l, pr = mid + 1;
    while(pos <= r){
	if(pl <= mid && (pr > r || p[pl].y < p[pr].y)){
	    if(p[pl].x > xmid - d) b[++pb] = p[pl];
	    a[pos++] = p[pl++];
	}
	else{
	    if(p[pr].x < xmid + d) c[++pc] = p[pr];
	    a[pos++] = p[pr++];
	}
    }
    for(int i = l; i <= r; i++) a[i] = p[i];
    for(int i = 1, j = 1; i <= pb || j <= pc;){
	if(i <= pb && (j > pc || b[i].y < c[j].y)){
	    for(int k = j - 1; k && b[i].y - c[k].y < d; k--)
		d = min(d, (b[i] - c[k]).norm());
	    i++;
	}
	else{
	    for(int k = i - 1; k && c[j].y - b[k].y < d; k--)
		d = min(d, (c[j] - b[k]).norm());
	    j++;
	}
    }
    return d;
}

int main(){

    read(n);
    for(int i = 1; i <= n; i++)
	scanf("%lf%lf", &p[i].x, &p[i].y);
    sort(p + 1, p + n + 1);
    printf("%.4lf\n", solve(1, n));

    return 0;
}