RSA 非对称加密算法简述

RSA概述

首先看这个加密算法的命名.很有意思,它其实是三个人的名字.早在1977年由麻省理工学院的三位数学家Rivest、Shamir 和 Adleman一起提出了这个加密算法,并且用他们三个人姓氏开头字母命名.

RSA加密算法是一种非对称加密算法,其玩法打破了以往所有加密算法的规则.在RSA出现之前,所有的加密方法都是同一种模式:加密解密的规则使用同一种方式.这种长达几个世纪的加密方案有一个致命的缺陷.在传递加密信息时,必须让对方拿到解密的规则才能正常解密.由于加密解密的规则一致,所以保存和传递"密钥"，就成了最头疼的问题。

RSA的出现解决了这个问题.我们来看看RSA是怎么玩的.

RSA加密/解密

使用公钥加密的数据,利用私钥进行解密
使用私钥加密的数据,利用公钥进行解密

没错,RSA加密使用了"一对"密钥.分别是公钥和私钥,这个公钥和私钥其实就是一组数字!其二进制位长度可以是1024位或者2048位.长度越长其加密强度越大,目前为止公之于众的能破解的最大长度为768位密钥,只要高于768位,相对就比较安全.所以目前为止,这种加密算法一直被广泛使用.

RSA的弊端

由于RSA算法的原理都是大数计算，使得RSA最快的情况也比对称加密算法慢上好几倍。速度一直是RSA的缺陷,一般来说RSA只用于小数据的加密.RSA的速度是对应同样安全级别的对称加密算法的1/1000左右。

RSA终端命令演示

由于Mac系统内置OpenSSL(开源加密库),所以我们可以直接在终端上使用命令来玩RSA.

OpenSSL中RSA算法常用指令主要有三个，其他指令此处不介绍。

命令	含义
genrsa	生成并输入一个RSA私钥
rsautl	使用RSA密钥进行加密、解密、签名和验证等运算
rsa	处理RSA密钥的格式转换等问题

显得非常高大上对吧!那么它里面是什么,我们可以利用终端进行查看.

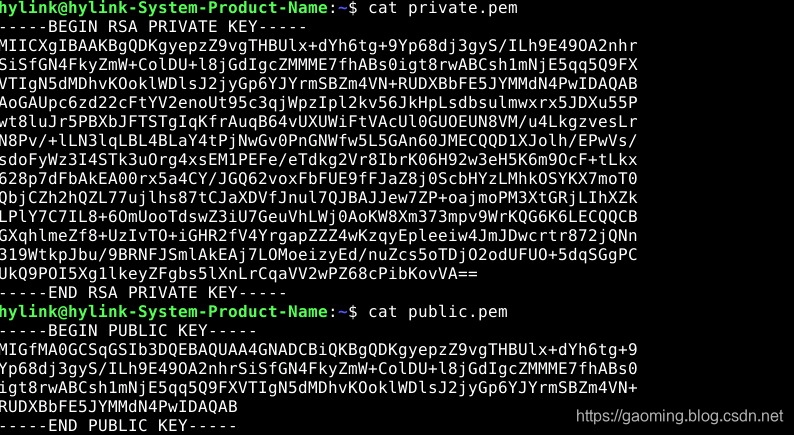
其实就是一个文本文件,并且一看就知道是base64编码.那么公钥相比私钥要简单很多.我们可以通过命令,将私钥转换成为明文看看

//转化为明文信息

openssl rsa -in private.pem -text -out private.txt

writing RSA key

//查看文本信息

cat private.txt

Private-Key: (1024 bit)

modulus:

00:ca:83:27:a9?9f:6f:81:31:c1:52:5c:7e:75:

88:7a:b6:0f:bd:62:9e:bc:76:3d:e0:c9:2f:c8:2e:

1f:44:e3:d3:80:da:78:6b:4a:24:9f:18??05:93:

26:66:5b:e0:a8:94:35:3e:97:c8:c6:74:88:1c:64:

c3:0c:13:b7:e1:00:1b:34:8a:0b:7c:af:00:01:0a:

c8:75:98:d8:c4:e6:aa:b9:43:d1:57:55:32:20:37:

97:4c:0e:1b:ca:3a:89:25:58:39:6c:27:68:f2:1a:

9e:98:25:8a:e6:48:16:66:e1:53:7e:45:40:d7:05:

b1:44:e4:96:0c:31:d3:78:3f

publicExponent: 65537 (0x10001)

privateExponent:

52:97:3a?dd:b6:70:5b:58:57:67:a7:a1:4b:7d:

e5?ea:8d:6a:73:22:99:76:92:fe:7a:26:41:e9:

2e:c7:5b:b2:e9:66:c3:1a:f1:e4:90:d7:bb:9e:4f:

c2:df:25:b8:9a:f9:3c:15:db:24:54:d2:4e:02:2a:

29:fa:c0:ba:a0:7a:e2:f5:17:51:68:85:b5:50:1c:

52:5d:06:50:e1:14:37:c5:4c:fe:ee:0b:92:0c:ef:

7a:c2:eb:37:c3:ef:ff:e9:4b:37:79:6a:2c:12:f8:

04:b6:98:e2:d3:e3:37:01:af:d0:f9:c6:35:67:f0:

e4:be:46:02:7e:b4:24:c1

prime1:

00:f5:5c:9a:25:87:f1:0f:c1:5b:3f:b1:da:05:c9:

6c:f7:23:84:93:93:7b:8e:ae:0e:31:b0:43:35:3c:

41:5e:fd:e4:dd:92:0d:95:af:c2:1b:ac:ad:3a:1f:

dd:b0:dd:e1:f9:2b:a9:bd:39:c1:7e:b4:b9:31:eb:

6f:29:ed:d1:5b

prime2:

00:d3:4a:f1:e5:ae:02:63:f2:46:43:ad:af:a3:11:

5b:15:41:3d:7c:52:5a:67:c8:f4:49:c6:c7:63:32:

cc:86:43:92:60:a5:fb:9a:84:f4:41:b8:c2:66:1d:

a1:41:92:fb:ee:e8:e5:86:cf:3b:b4:22:5a:5c:35:

5f:26:7b:a5:ed

exponent1:

00:92:5e:c3:b6:4f:fa:86:a3:9a:83:cc:dd:7b:46:

46:32:c8:85:76:64:2c:f9:58:ec:2e:c8:2f:cf:ba:

3a:65:28:a1:37:6c:c1:9d:e2:53:b1:9e:b9:58:4b:

5a:3d:00:a0:a5:bc:5e:6d:fb??6a:6f:f5:6a:ca:

40:6e:8a:e8:b1

exponent2:

00:81:19:7a:a1:96:67:99:7f:cf:94:cc:8b:d3:3b:

e8:86:1d:1d:9f:57:86:2b:81:aa:59:65:9e:30:2b:

3a:b2:12:99:5e:7a:2c:38:26:62:43:c1:ca:ed:af:

ce:f6:8d:03:67:df:5f:56:b6:4a:49:6e:ef:fd:05:

13:45:25:29:a5

coefficient:

00:8f:b2:ce:32:87:a2:cf:21:1d:fe:7b:99:72:ce:

68:4c:38:ce:da:87:54:15:43:be:e5:da:92:1a:03:

c2:52:44:3d:3c:e2:39:5e:0d:65:91:ec:99:16:06:

ec:e6:55:e7:2e:b0:aa:69:55:76:c0:f6:7a:f1:c3:

e2:6c:aa:2f:54

-----BEGIN RSA PRIVATE KEY-----

MIICXgIBAAKBgQDKgyepzZ9vgTHBUlx+dYh6tg+9Yp68dj3gyS/ILh9E49OA2nhr

SiSfGN4FkyZmW+ColDU+l8jGdIgcZMMME7fhABs0igt8rwABCsh1mNjE5qq5Q9FX

VTIgN5dMDhvKOoklWDlsJ2jyGp6YJYrmSBZm4VN+RUDXBbFE5JYMMdN4PwIDAQAB

AoGAUpc6zd22cFtYV2enoUt95c3qjWpzIpl2kv56JkHpLsdbsulmwxrx5JDXu55P

wt8luJr5PBXbJFTSTgIqKfrAuqB64vUXUWiFtVAcUl0GUOEUN8VM/u4LkgzvesLr

N8Pv/+lLN3lqLBL4BLaY4tPjNwGv0PnGNWfw5L5GAn60JMECQQD1XJolh/EPwVs/

sdoFyWz3I4STk3uOrg4xsEM1PEFe/eTdkg2Vr8IbrK06H92w3eH5K6m9OcF+tLkx

628p7dFbAkEA00rx5a4CY/JGQ62voxFbFUE9fFJaZ8j0ScbHYzLMhkOSYKX7moT0

QbjCZh2hQZL77ujlhs87tCJaXDVfJnul7QJBAJJew7ZP+oajmoPM3XtGRjLIhXZk

LPlY7C7IL8+6OmUooTdswZ3iU7GeuVhLWj0AoKW8Xm373mpv9WrKQG6K6LECQQCB

GXqhlmeZf8+UzIvTO+iGHR2fV4YrgapZZZ4wKzqyEpleeiw4JmJDwcrtr872jQNn

319WtkpJbu/9BRNFJSmlAkEAj7LOMoeizyEd/nuZcs5oTDjO2odUFUO+5dqSGgPC

UkQ9POI5Xg1lkeyZFgbs5lXnLrCqaVV2wPZ68cPibKovVA==

-----END RSA PRIVATE KEY-----

通过公钥加密数据,私钥解密数据

//新建文件，内容为123456

vi message.txt

//查看原文件内容

cat message.txt

//通过公钥进行加密

hank$ openssl rsautl -encrypt -in message.txt -inkey public.pem -pubin -out enc.txt

//通过私钥进行解密

hank$ openssl rsautl -decrypt -in enc.txt -inkey private.pem -out dec.txt

//查看解密后的文件内容

cat dec.txt

通过私钥加密数据,公钥解密数据

//通过私钥进行加密

openssl rsautl -sign -in message.txt -inkey private.pem -out enc.txt

//通过公钥进行解密

openssl rsautl -verify -in enc.txt -inkey public.pem -pubin -out dec.txt

小结

由于RSA加密运行效率非常低!并不是所有数据加密都会使用它.那么它的主战场在于加密一些小的数据,比如对称加密算法的密钥.又或者数字签名.