【HDU6701】Make Rounddog Happy【权值线段树+双向单调队列】

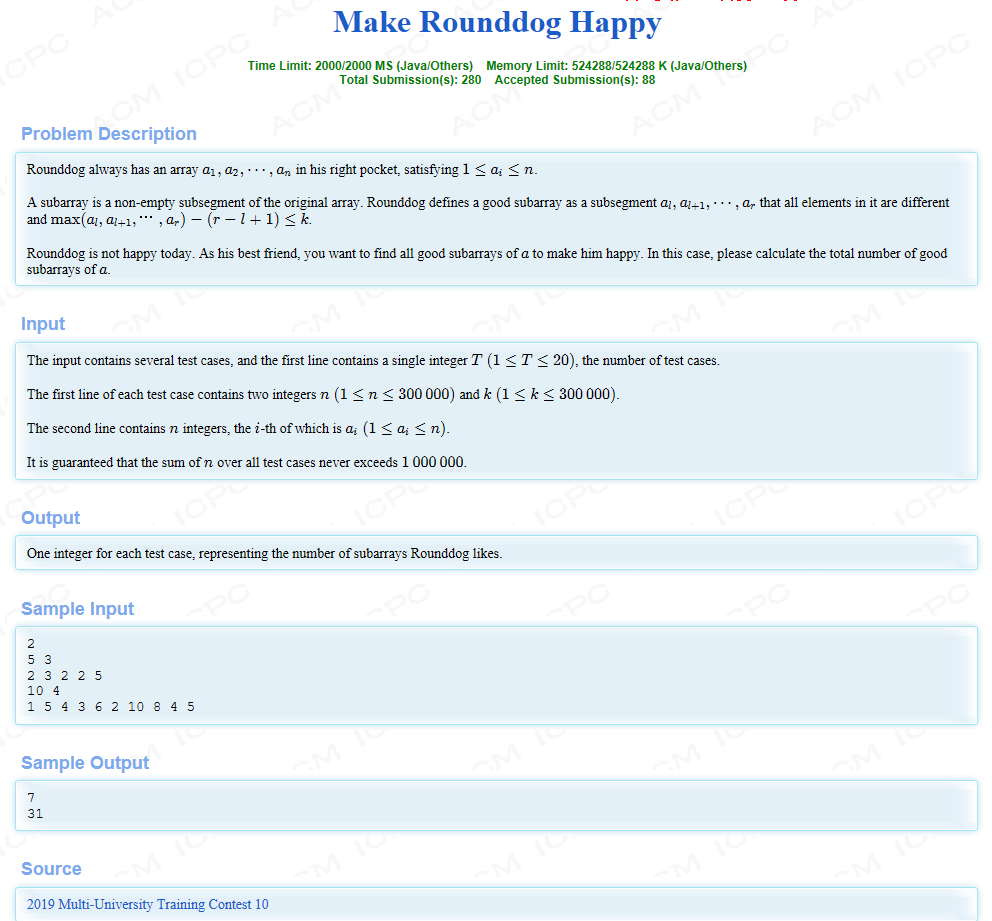
题意：给你一个序列，求满足要求的子序列个数，其中要求为：

1、子序列的max-子序列长度len<=k

2、子序列中不出现重复的数字

题解：首先看到子序列max，很容易想到枚举最大值然后分治，这个做法有人通过，但是我并没想到如何做

子序列max还有一个思路是单调队列，这里我们通过单调队列进行解题

首先对于给出的限制条件式子max-(r-l+1)<=k，我们进行移项，可得max+l<=k+r+1，此时我们将l和r分离至不等式两边

容易看出我们可以枚举右端点，然后维护一个权值线段树，每次只需要查询1~k+r+1区间的sum就可以了

以max+l作为权值建线段树

那么容易想到用单调队列进行维护max，每次更新单调队列的时候相当于在权值线段树上的一个区间进行+1/-1操作

单调队列维护：值，位置，这个值的左端点

维护单调队列时为了满足子序列不出现重复数字，于是考虑双向单调队列

新枚举右端点时，单调队列从右往左退栈，直到第一个不小于右端点数字的位置

然后考虑此时的最左边能到哪里

考虑记下每一个位置的前驱位置，即前一个相同数字在哪

容易想到维护一个最大值表示当前的最左端点在哪，每新枚举一个右端点，那么将last[i]+1和当前的左端点取个max，即为新的左端点，显然这样是当前右端点下最大的满足条件的左端点

于是单调队列从左往右退栈，直到第一个下标大于等于左端点的位置，然后再更新单调队列里维护的左端点

至此则可以在nlogn的时间内求出答案

时间复杂度O(nlogn)

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#define ll long long
using namespace std;
int T;
int n,k;
int a[],last[],hd[];
int lh[],mx[],mxi[],ln,rn;
ll ans;
class Segtree
{
public:
    ll v[*],flv[*];
    bool fl[*];

    void init()
    {
        memset(v,,sizeof(v));
        memset(fl,,sizeof(fl));
        memset(flv,,sizeof(flv));
    }
    void pushdown(int l,int r,int pos)
    {
        if(fl[pos])
        {
          int mid=l+r>>;
          v[pos<<]+=flv[pos]*(mid-l+);
          v[pos<<|]+=flv[pos]*(r-mid);
          flv[pos<<]+=flv[pos];
          flv[pos<<|]+=flv[pos];
          fl[pos<<]=fl[pos<<|]=;
          fl[pos]=;flv[pos]=;
        }
    }
    void pushup(int pos)
    {
        v[pos]=v[pos<<]+v[pos<<|];
    }
    void change(int l,int r,int al,int ar,ll tv,int pos)
    {
        if(l==al && r==ar)
        {
          v[pos]+=tv*(ar-al+);
          fl[pos]=;
          flv[pos]+=tv;
          return;
        }
        pushdown(l,r,pos);
        int mid=l+r>>;
        if(ar<=mid)change(l,mid,al,ar,tv,pos<<);
        if(al>mid)change(mid+,r,al,ar,tv,pos<<|);
        if(al<=mid && ar>mid)
        {
          change(l,mid,al,mid,tv,pos<<);
          change(mid+,r,mid+,ar,tv,pos<<|);
        }
        pushup(pos);
    }
    ll ask(int l,int r,int al,int ar,int pos)
    {
        if(l==al && r==ar)return v[pos];
        int mid=l+r>>;
        pushdown(l,r,pos);
        if(ar<=mid)return ask(l,mid,al,ar,pos<<);
        if(al>mid)return ask(mid+,r,al,ar,pos<<|);
        if(al<=mid && ar>mid)return ask(l,mid,al,mid,pos<<)+ask(mid+,r,mid+,ar,pos<<|);
    }
}segtree;
int main()
{
    scanf("%d",&T);
    while(T--)
    {
      segtree.init();
      ans=;
      memset(hd,,sizeof(hd));
      memset(last,,sizeof(last));
      scanf("%d%d",&n,&k);
      for(int i=;i<=n;i++)
      {
        scanf("%d",&a[i]);
        last[i]=hd[a[i]];
        hd[a[i]]=i;
      }
      ln=;rn=;int tl,tl2=;
      for(int i=;i<=n;i++)
      {
        tl=i;tl2=max(tl2,last[i]+);
        while(ln<=rn && mx[rn]<a[i])
        {
          tl=min(tl,lh[rn]);
          segtree.change(,n*,mx[rn]+lh[rn],mx[rn]+mxi[rn],-,);
          rn--;
        }
        segtree.change(,n*,a[i]+tl,a[i]+i,,);
        rn++;
        lh[rn]=tl;mx[rn]=a[i];mxi[rn]=i;
        while(ln<=rn && mxi[ln]<tl2)
        {
          segtree.change(,n*,mx[ln]+lh[ln],mx[ln]+mxi[ln],-,);
          ln++;
        }
        if(ln<=rn && lh[ln]<tl2)
        {
          segtree.change(,n*,mx[ln]+lh[ln],mx[ln]+tl2-,-,);
          lh[ln]=tl2;
        }
        ans+=segtree.ask(,n*,,min(i+k+,n*),);
      }
      printf("%lld\n",ans);
    }
    return ;
}

心得：区间max的处理方法不仅有枚举max然后分治，还有单调队列，思维不要唯一，要多想一些