从最大似然函数 到 EM算法详解

极大似然算法

---

本来打算把别人讲的好的博文放在上面的，但是感觉那个适合看着玩，我看过之后感觉懂了，然后实际应用就不会了。。。。

　　　　MLP其实就是用来求模型参数的，核心就是“模型已知，求取参数”，模型的意思就是数据符合什么函数，比如我们硬币的正反就是二项分布模型，再比如我们平时随机生成的一类数据符合高斯模型。。。

　　　　直接上公式：

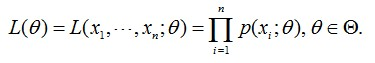
　　　　　L(Θ) ：联合概率分布函数，就是每个样本出现的概率乘积。

　　　  x₁,x₂,x₃....x_n  : 样本

　　　  Θ ： 模型的参数（比如高斯模型的两个参数：μ、σ）

　　　  p(x_i ; Θ) : 第i个样本的概率模型

　　　  xi ：第i个样本

　　平时使用的时候取对数，完全为了求解方便。（从后面可以看出求导方便）：

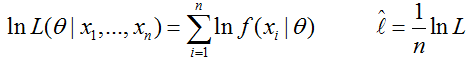
　　  而称为平均对数似然。而我们平时所称的最大似然为最大的对数平均似然，即：

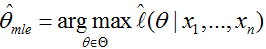
　　举例一：　

举一个抛硬币的简单例子。 现在有一个正反面不是很匀称的硬币，如果正面朝上记为H，方面朝上记为T，抛10次的结果如下：

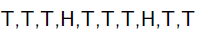
求这个硬币正面朝上的概率有多大？

很显然这个概率是0.2。现在我们用MLE的思想去求解它。我们知道每次抛硬币都是一次二项分布，设正面朝上的概率是，那么似然函数为：

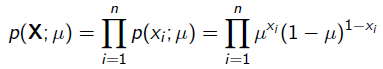
x=1表示正面朝上，x=0表示方面朝上。那么有：

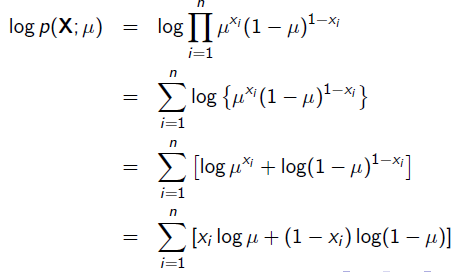
求导：

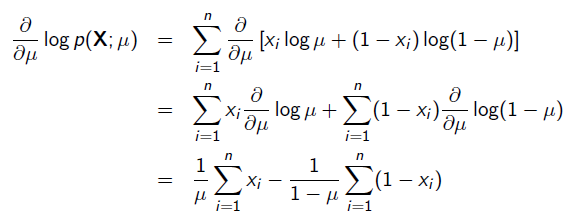
令导数为0，很容易得到：

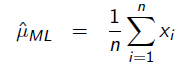
也就是0.2 。

举例二：

假如我们有一组连续变量的采样值（x1,x2,…,xn），我们知道这组数据服从正态分布，标准差已知。请问这个正态分布的期望值为多少时，产生这个已有数据的概率最大？

　　　　P(Data | M) = ？

根据公式：

　　 

可得:

　　对μ求导可得：

则最大似然估计的结果为μ=(x1+x2+…+xn)/n

　　举例三：

　　　　　　　　

　　假设我们要统计全国人民的年均收入，首先假设这个收入服从服从正态分布，但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的收入。我们国家有10几亿人口呢？那么岂不是没有办法了？

不不不，有了极大似然估计之后，我们可以采用嘛！我们比如选取一个城市，或者一个乡镇的人口收入，作为我们的观察样本结果。然后通过最大似然估计来获取上述假设中的正态分布的参数。

有了参数的结果后，我们就可以知道该正态分布的期望和方差了。也就是我们通过了一个小样本的采样，反过来知道了全国人民年收入的一系列重要的数学指标量！

那么我们就知道了极大似然估计的核心关键就是对于一些情况，样本太多，无法得出分布的参数值，可以采样小样本后，利用极大似然估计获取假设中分布的参数值。

　　　　注：最大似然函数真的很简单，刚开始我也一头雾水。其实我们用的很多函数都可以说是一个最大似然函数，比如符合y = x²、y = kx。。。。都可以当做一个模型去求解一个极大似然函数，只不过我们得到的数据不符合这些模型而已。

　　　　大家有没有发现只要是求概率的问题，都会写出一个函数，这个函数其实就是最大似然函数，可以说是目标函数，也可以说是似然函数，把每个数据出现的概率相乘就是似然函数，再求对数，再求均值，再求最值，这就是极大似然了，就是一个名字而已！

EM算法概述

---

　　　　EM算法核心：猜（E-step）,反思（M-step）,重复；

　　先说说我自己对EM算法的理解：

　　　　问题一：

　　现在一个班里有50个男生，50个女生，且男生站左，女生站右。我们假定男生的身高服从正态分布 ，女生的身高则服从另一个正态分布： 。这时候我们可以用极大似然法（MLE），分别通过这50个男生和50个女生的样本来估计这两个正态分布的参数。

  问题二：

　　但现在我们让情况复杂一点，就是这50个男生和50个女生混在一起了。我们拥有100个人的身高数据，却不知道这100个人每一个是男生还是女生。这时候情况就有点尴尬，因为通常来说，我们只有知道了精确的男女身高的正态分布参数我们才能知道每一个人更有可能是男生还是女生。但从另一方面去考量，我们只有知道了每个人是男生还是女生才能尽可能准确地估计男女各自身高的正态分布的参数。

　　问题二需要求解两个问题：

　　　　假设a=（第k个样本是男生还是女生）

　　　　假设b=（高斯模型的参数）

　　如果知道a，那用问题一的方法就可以求解b，如果知道b那也就可以分类a了，但是前提是两个都不知道。。。。比如y=x+1，现在让你求解x和y的值，怎么办？

　　　　　 解决：

　　　　　

　　　　总结：其实EM算法就是先通过假设的参数（不能太无厘头了）把数据进行分类，然后通过分类的数据计算参数，接着对比计算的参数和假设的参数是否满足精度，不满足就返回去，满足就结束。

　　　　　　　　EM算法使用简单，但是证明很麻烦，我感觉没必要去证明，会使用就好了，反正EM是一种思想，而不是像K-means等是一种算法。

参考：

　　　　1.http://blog.csdn.net/zouxy09/article/details/8537620（本博文的核心都来自这里，说的通俗易懂！）

　　　　2.http://www.cnblogs.com/sylvanas2012/p/5058065.html（最大似然的举例1）

　　　　3.http://blog.csdn.net/qq_18343569/article/details/49981507（最大似然的举例2）

　　　　　4.https://www.zhihu.com/question/27976634/answer/154998358（EM算法的问题来源知乎，但是作者没有解决）

　　　　5.http://www.jianshu.com/p/1121509ac1dc（还没来得及看的EM例子，排版很好，不知道内容）