丑数问题 Ugly Number

2018-07-28 15:30:21

一、判断是否为丑数

问题描述：

问题求解：

所谓丑数，首先得是正数，然后其质数因子只包含了2，3，4，因此我们只需要对当前的数分别除2，3，4直到不能除为止。

    public boolean isUgly(int num) {
        if (num > 0) {
            for (int i = 2; i < 6; i++) {
                while (num % i == 0) num /= i;
            }
        }
        return num == 1;
    }

二、第n个丑数

问题描述：

问题求解：

由上面检测丑数的解法我们可以知道，每次丑数的生成都是使用2，3，5来乘已经生成的丑数，取其中最小的。为了降低不必要的比较，我们需要将当前2，3，5需要乘的丑数的下标保存下来，利用下标来进行快速的计算和判断。

    public int nthUglyNumber(int n) {
        int[] res = new int[n];
        int[] idx = new int[3];
        res[0] = 1;
        for (int i = 1; i < n; i++) {
            res[i] = Math.min(2 * res[idx[0]], Math.min(3 * res[idx[1]], 5 * res[idx[2]]));
            if (res[i] == 2 * res[idx[0]]) idx[0]++;
            if (res[i] == 3 * res[idx[1]]) idx[1]++;
            if (res[i] == 5 * res[idx[2]]) idx[2]++;
        }
        return res[n - 1];
    }

三、丑数问题的扩展

问题描述：

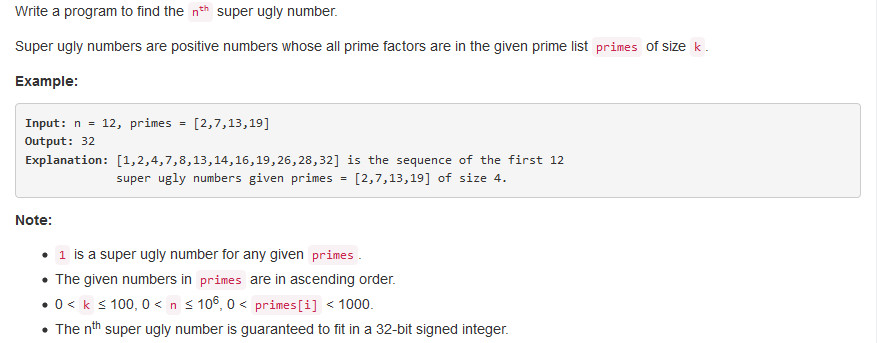
问题求解：

本题其实就是将丑数问题中质数从2，3，5扩展到了primes数组，本质的解法是一样的。

    public int nthSuperUglyNumber(int n, int[] primes) {
        int[] res = new int[n];
        int[] idx = new int[primes.length];
        res[0] = 1;
        for (int i = 1; i < n; i++) {
            res[i] = Integer.MAX_VALUE;
            for (int j = 0; j < primes.length; j++) {
                res[i] = Math.min(res[i], primes[j] * res[idx[j]]);
            }
            for (int j = 0; j < primes.length; j++) {
                if (primes[j] * res[idx[j]] <= res[i]) idx[j]++;
            }
        }
        return res[n - 1];
    }

这里可以对内层循环进行优化，将两次循环降低到一次循环，要做到这一步，就需要再申请大小为primes.length的数组，用来保存当前乘积。

    public int nthSuperUglyNumber2(int n, int[] primes) {
        int[] res = new int[n];
        int[] idx = new int[primes.length];
        int[] val = new int[primes.length];
        Arrays.fill(val, 1);
        int next = 1;
        for (int i = 0; i < n; i++) {
            res[i] = next;
            next = Integer.MAX_VALUE;
            for (int j = 0; j < primes.length; j++) {
                if (val[j] == res[i]) val[j] = primes[j] * res[idx[j]++];
                next = Math.min(next, val[j]);
            }
        }
        return res[n - 1];
    }