ACM International Collegiate Programming Contest World Finals 2014

ACM International Collegiate Programming Contest World Finals 2014

A - Baggage

题目描述：有\(2n\)个字符摆在编号为\(1\)~\(2n\)格子里，奇数位为\(B\)，偶数位为\(A\)，另外编号为\((-2n+1)\)~\(0\)的格子是空的，现在可以移动两个相邻的字符，移动到两个空的格子里，最终使得全部\(A\)在全部\(B\)的左边，而且字符都是连续的，但不必放回原位，输出最小步数的方案。

solution
显然，最小操作为\(n\)步。
假设\(n=8\)，
__BABABABABABABABA

ABBABABABABABAB__A

ABBA__BABABABABBAA

ABBA|__BABABABA|BBAA

如果存在一种方案使得中间字变成下面的模样，即两个空位跑到了最后
ABBA|AAAABBBB__|BBAA

A__AAAAABBBBBBBBAA

AAAAAAAABBBBBBBB__

最后两位也是空位。四步解决八个字符（四个\(A\)，四个\(B\)），也就是可以递归求解方案。

但要特殊处理\(n=3, 4, 5, 6, 7\)的方案，因为这几个的操作比较特殊，最优操作并不是上述的操作，这几个特殊的可以暴搜出来。

时间复杂度：\(O(n)\)

B - Buffed Buffet

题目描述：有\(n\)道菜，这\(n\)道菜可以分成两类，第一类是以整数为计量，即一道这样的菜有一个固定的重量\(\omega_i\)，若这道菜点了\(m\)道，则第\(j\)道的美味值为\(t_i-j\Delta t\)；第二类是以小数为计量，即这道菜可以取任意一个重量\(X\)，则这道菜的美味值为\(\int_{0}^{X} (t_i-x\Delta t) dt\)。问在菜的总质量为\(W\)的情况下，美味值最大是多少。

solution
先解决第一类的菜。
这看起来像一个普通的背包，但直接\(O(nW^2)\)会超时。可以考虑将菜按重量分类，重量相同的菜各自算出第\(j\)道菜的美味值，因为这些菜的重量是相同的，所以取（相同重量的菜）算出来的美味值的前\(W\)个即可。这样归类之后，最多有\(n\)种重量不同的菜，所以背包的时间复杂度为\(O(\sum_{w=1}^{W} wlnn)=O(\frac{1}{2}W^2lnn)\)
然后解决第二类菜。
枚举第一类菜的总重量\(wf\)，剩下的重量由第二类的菜来承担。
因为是重量是连续的，考虑用拉格朗日乘数法。设每种菜的重量为\(x_i\)，
约束函数
\[g(x_i)=\sum x_i-(W-wf)=0\]
目标函数为
\[f(x_i)=\sum \frac{1}{2}(2t_i-x_i\Delta t)x_i\]
设函数
\[F(x_i)=f(x_i)-\lambda g(x_i)\]
求解得
\[x_i=\frac{t_i-\lambda }{\Delta t}\]
但因为\(x_i \geq 0\)，所以选择用二分的方法来求解\(\lambda\)，在这里\(\lambda\)有一个特殊的几何意义：每道菜只取美味函数（美味值的被积函数）大于等于\(\lambda\)的部分，若某道菜的\(t_i<\lambda\)，则\(x_i=0\)。\(\lambda\)越小，\(g(x_i)\)越能满足。
但有一类特殊的菜需要注意，就是\(\Delta t=0\)的菜，这些菜的美味函数是一个常数函数，这些菜不能用上面的方法来求解（因为\(\Delta t\)在\(x_i\)的分母）。显然，这类菜只需考虑\(t_i\)最大值（\(con\)）即可，当\(\lambda > con\)时，就不必选这道菜了，否则\(\lambda < con\)的部分可以用这道菜来补充，所以可以令\(\lambda =con\)，算出\(\sum x_i, (W-wf)-\sum x_i\)的部分由\(con\)来补充，更新答案。

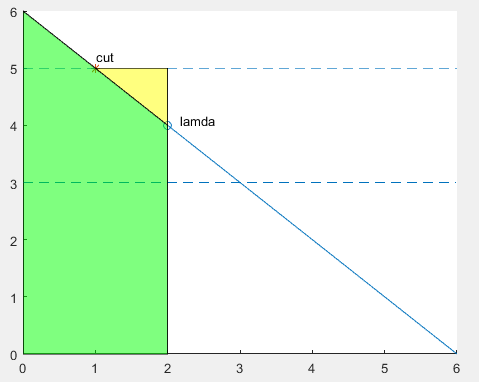
如图\(cut\)表示\(con>\lambda\)的情况，此时菜只选到\(cut\)就好，剩余的部分可由\(con\)补充，这样美味值就能增加黄色部分。

时间复杂度：\(O(W^2lnn+Wnlog(2*10^{16}))，2*10^{16}=2*10^8*10^8\)，前一个\(2*10^8\)表示\(\lambda\)的范围，后一个\(10^8\)表示精度范围。

C - Crane Balancing

题目描述：给出一个在二维平面上的多边形，在平面上\(1 \times 1\)的正方形的重量为\(1\)，现在在多边形上指定一个顶点，在这个顶点上放一定质量的物体（无体积），满足多边形不向两边倒，问物体质量的范围，或无论质量是多少都会倒（unstable)

solution
将多边形剖分成很多个三角形，有向面积就是有向重量，然后求出三角形的质心（坐标平均），然后求出这些质点的质心，这个质心就是多边形的质心。找出多边形在\(y\)轴上的点，只有最左边和最右边的点才可能成为支点。多边形的质心与指定顶点构成的新质心的\(x\)坐标一定要在这两个支点之间，多边形才不会倒。
所以分类判断多边形的质心是否在两个支点之间，再根据指定的顶点再分类讨论，注意讨论指定顶点的\(x\)坐标是否在支点上。

时间复杂度：\(O(n)\)

D - Game Strategy

题目描述：有\(n\)个点，每个点有若干个集合(总共有\(m\)个)。有两个人在玩游戏，一开始指针在某一个点，第一个人这个点的一个集合，第二人选择这个集合内的一个点，然后指针移向那个点。分别求出从每个点出发，其它点能否到达，如果能则输出最小步数，否则输出\(-1\)。（第二个人是阻止第一个人的）

solution
显然如果能到达某个点，则最小步数不超过\(n\)，所以可以一步一步地走。显然答案是最长路径，然后暴力搜就好了。

时间复杂度：\(O(n^2m)\)

I - Sensor Network

题目描述：求一个无向图的最大团。

solution
随机一种\(n\)排列，然后按排列顺序构最大团。

时间复杂度：\(O(n^2*10000)\)

K - Surveillance

题目描述：给出\(n\)个数对\((a, b)\)，如果\(a \leq b\)，则表示区间\([a, b]\)，如果\(a>b\)，则表示区间\([1, b], [a, m]\)，问最少需要多少个数对覆盖\([1, m]\)。

solution
将区间延长至\([1, 2m]\)，则一个数对对应一个区间。那么问题变成最少区间覆盖一个长度至少为\(m\)的连续区间。
将区间按右端点排序，然后倍增求出一个区间\(i\)出发向左利用\(2^j\)个区间最左能到哪个区间，以及最长能覆盖多长的区间。然后再倍增求答案即可。

时间复杂度：\(O(nlogn)\)