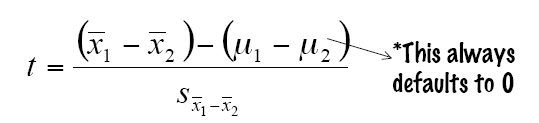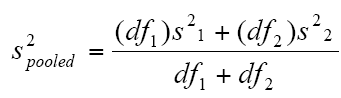数据分析之可反复与独立样本的T-Test分析

版权声明：本文为博主原创文章，未经博主同意不得转载。 https://blog.csdn.net/jia20003/article/details/24201297

数据分析之独立样本的T-Test分析

比較两个独立样本数据之间是否有显著性差异，将实验数据与标准数据对照，查看

实验结果是否符合预期。T-Test在生物数据分析。实验数据效果验证中非经常见的数

据处理方法。http://www.statisticslectures.com/tables/ttable/ - T-table查找表

独立样本T-test条件：

1.      每一个样本相互独立没有影响

2.      样本大致符合正态分布曲线

3.      具有同方差异性

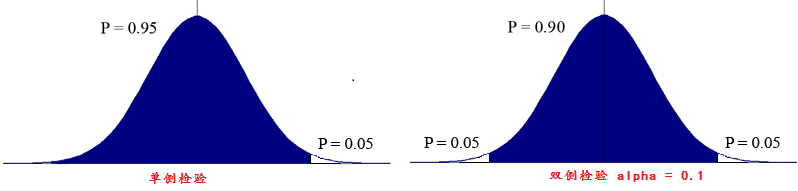
单側检验(one-tail Test)与双側检验(Two-Tail Test)

基本步骤：

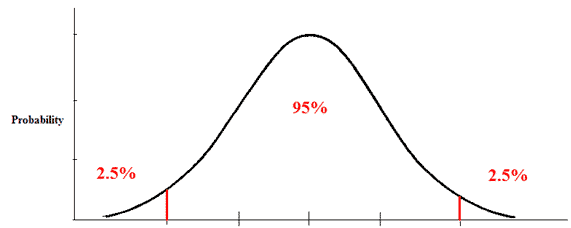
1.双側检验, 条件声明  alpha值设置为0.05

依据t-table, alpha = 0.05, df = 38时, 对于t-table的值为2.0244

2. 计算自由度(Degree of Freedom)

Df = （样本1的总数 + 样本2的总数）- 2

3. 声明决策规则

假设计算出来的结果t-value的结果大于2.0244或者小于-2.0244则拒绝

4. 计算T-test统计值

5. 得出结论

假设计算结果在双側区间之内，说明两组样本之间没有显著差异。

可反复样本的T-Test计算

相同一组数据在不同的条件下得到结果进行比对，发现是否有显著性差异，最常见

的对一个人在饮酒与不饮酒条件下驾驶车辆測试，非常easy得出酒精对驾驶员有显著

影响 

算法实现：

对独立样本的T-Test计算最重要的是计算各自的方差与自由度df1与df2

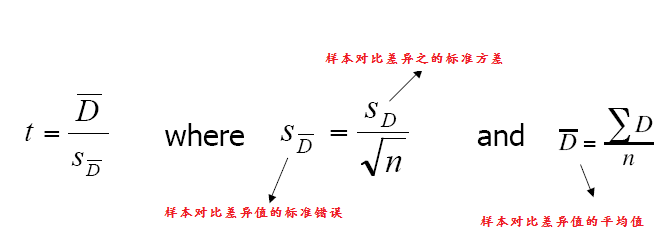
对可反复样本的对照t-test计算

程序实现：

 

package com.gloomyfish.data.mining.analysis;

public class TTestAnalysisAlg {

	private double alpahValue = 0.05; // default
	private boolean dependency = false; // default

	public TTestAnalysisAlg() {
		System.out.println("t-test algorithm");
	}

	public double getAlpahValue() {
		return alpahValue;
	}

	public void setAlpahValue(double alpahValue) {
		this.alpahValue = alpahValue;
	}

	public boolean isDependency() {
		return dependency;
	}

	public void setDependency(boolean dependency) {
		this.dependency = dependency;
	}

	public double analysis(double[] data1, double[] data2) {
		double tValue = 0;
		if (dependency) {
			// Repeated Measures T-test.
			// Uses the same sample of subjects measured on two different
			// occasions
			double diffSum = 0.0;
			double diffMean = 0.0;
			int size = Math.min(data1.length, data2.length);
			double[] diff = new double[size];
			for(int i=0; i<size; i++)
			{
				diff[i] = data2[i] -data1[i];
				diffSum += data2[i] -data1[i];
			}
			diffMean = diffSum / size;
			diffSum = 0.0;
			for(int i=0; i<size; i++)
			{
				diffSum += Math.pow((diff[i] -diffMean), 2);
			}
			double diffSD = Math.sqrt(diffSum / (size - 1.0));
			double diffSE = diffSD / Math.sqrt(size);
			tValue = diffMean / diffSE;

		} else {

			double means1 = 0;
			double means2 = 0;
			double sum1 = 0;
			double sum2 = 0;

			// calcuate means
			for (int i = 0; i < data1.length; i++) {
				sum1 += data1[i];
			}

			for (int i = 0; i < data2.length; i++) {
				sum2 += data2[i];
			}

			means1 = sum1 / data1.length;
			means2 = sum2 / data2.length;

			// calculate SD (Standard Deviation)
			sum1 = 0.0;
			sum2 = 0.0;

			for (int i = 0; i < data1.length; i++) {
				sum1 += Math.pow((means1 - data1[i]), 2);
			}

			for (int i = 0; i < data2.length; i++) {
				sum2 += Math.pow((means2 - data2[i]), 2);
			}

			double sd1 = Math.sqrt(sum1 / (data1.length - 1.0));
			double sd2 = Math.sqrt(sum2 / (data2.length - 1.0));

			// calculate SE (Standard Error)
			double se1 = sd1 / Math.sqrt(data1.length);
			double se2 = sd2 / Math.sqrt(data2.length);
			System.out.println("Data Sample one - > Means :" + means1
					+ " SD : " + sd1 + " SE : " + se1);
			System.out.println("Data Sample two - > Means :" + means2
					+ " SD : " + sd2 + " SE : " + se2);

			// degree of freedom
			double df1 = data1.length - 1;
			double df2 = data2.length - 1;

			// Calculate the estimated standard error of the difference
			double spooled2 = (sd1 * sd1 * df1 + sd2 * sd2 * df2) / (df1 + df2);
			double Sm12 = Math.sqrt((spooled2 / df1 + spooled2 / df2));
			tValue = (means1 - means2) / Sm12;
		}

		System.out.println("t-test value : " + tValue);
		return tValue;

	}

	public static void main(String[] args) {
		int size = 10;
		System.out.println(Math.sqrt(size));
	}

}

測试程序：

package com.gloomyfish.dataming.study;

import com.gloomyfish.data.mining.analysis.TTestAnalysisAlg;

public class TTestDemo {

	public static double[] data1 = new double[]{
		35, 40, 12, 15, 21, 14, 46, 10, 28, 48, 16, 30, 32, 48, 31, 22, 12, 39, 19, 25
	};
	public static double[] data2 = new double[]{
		2, 27, 38, 31, 1, 19, 1, 34, 3, 1, 2, 3, 2, 1, 2, 1, 3, 29, 37, 2
	};
	public static void main(String[] args)
	{
		TTestAnalysisAlg tTest = new TTestAnalysisAlg();
		tTest.analysis(data1, data2);
		tTest.setDependency(true);
		double[] d1 = new double[]{2, 0, 4, 2, 3};
		double[] d2 = new double[]{8, 4, 11, 5, 8};

		//	The critical value for a one-tailed t-test with
		//	df=4 and α=.05 is 2.132
		double t = tTest.analysis(d1, d2);
		if(t > 2.132 || t < -2.132)
		{
			System.err.println("Very Bad!!!!");
		}
	}

}