codeforces#1139F. Dish Shopping （离散化数组数组+ 扫描线）

膜拜大佬：https://blog.csdn.net/xyz32768/article/details/88831233

题目链接：

http://codeforces.com/contest/1139/problem/F

题意：

有n个物品，物品有三个属性分别是$p_i，s_i，b_i$

有m个人，人有两个属性分别是$pref_j$，$inc_j$

一个人能买某个物品必须满足:，

$p_i \leq inc_j \leq s_i$

$|b_i-pref_j| \leq (inc_j-p_i)$

求出每个人能买物品的数量、

数据范围：

$1 \leq n \leq 10^5$

$1 \leq m \leq 10^5$

其它都是$1$到$10^9$

分析：

借用大佬的图片，描述物品的影响：

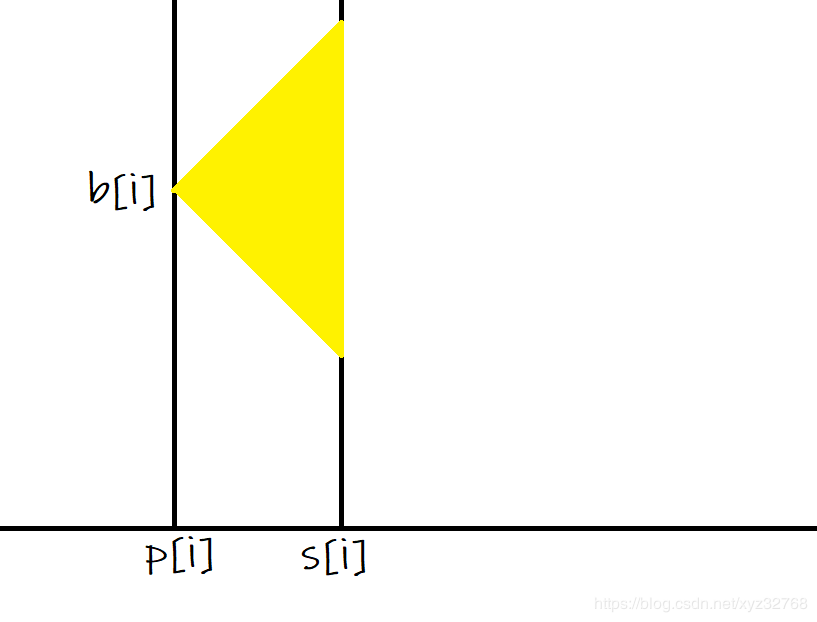
对$p_i,s_i,inc_j$进行扫描线处理，$p_i$时提取出$b_i$的影响，$s_i$时取消$b_i$的影响，$inc_j$时对$j$进行计算答案，计算$pref_j$在几个黄色三角形的影响里面。

一个点$（x，y）$受$b_i$影响需要满足下面的条件：

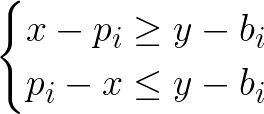
$x-y\geq p_i-b_i$时，$b_i$的影响加一

$-x-y\geq -p_i-b_i+1$时，$b_i$的影响减一

对这两个影响条件分别建立一个离散化的数状数组

具体实现看代码

ac代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
struct Node
{
    int is,id,x;
    bool operator <(const Node &a)const
    {
        if(x!=a.x)return x<a.x;
        else return is<a.is;
    }
};
int a[maxn*4],s[maxn],p[maxn],inc[maxn],b[maxn],treea[maxn*4],treeb[maxn*4],pb[maxn];
int ans[maxn];
map<int,int>ma;
int cnt=0,tt=0;
Node que[maxn*3];
int getid(int x)
{
    x=-x;
    return ma[x];
}
void add1(int x,int y)
{
    for(int i=x;i<4*maxn;i+=(i&-i))treea[i]+=y;
}
void add2(int x,int y)
{
    for(int i=x;i<4*maxn;i+=(i&-i))treeb[i]+=-y;
}
int quer1(int x)
{
    int res=0;
    for(int i=x;i>=1;i-=(i&-i))res+=treea[i];
    return res;
}
int quer2(int x)
{
    int res=0;
    for(int i=x;i>=1;i-=(i&-i))res+=treeb[i];
    return res;
}
int main()
{
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%d",&p[i]);
    for(int i=1;i<=n;i++)scanf("%d",&s[i]);
    for(int i=1;i<=n;i++)scanf("%d",&b[i]);
    for(int i=1;i<=m;i++)scanf("%d",&inc[i]);
    for(int i=1;i<=m;i++)scanf("%d",&pb[i]);

    for(int i=1;i<=n;i++)
    {
        a[++cnt]=-(p[i]+b[i]-1),a[++cnt]=-(b[i]-p[i]);
        que[++tt]=Node{0,i,p[i]};
        que[++tt]=Node{2,i,s[i]};
    }

    for(int i=1;i<=m;i++)
    {
        a[++cnt]=-(inc[i]+pb[i]),a[++cnt]=-(pb[i]-inc[i]);
        que[++tt]=Node{1,i,inc[i]};
    }
    sort(que+1,que+1+tt);
    sort(a+1,a+cnt+1);
    int pz=1;
    for(int i=1;i<=cnt;i++)
        if(ma[a[i]]==0)ma[a[i]]=pz++;

    for(int i=1;i<=tt;i++)
    {

        Node now=que[i];
        if(now.is==0)
        {
            add1(getid(b[now.id]-p[now.id]),1);
            add2(getid(p[now.id]+b[now.id]-1),1);
        }
        else if(now.is==1)
        {
            ans[now.id]=quer1(getid(pb[now.id]-inc[now.id]))+quer2(getid(inc[now.id]+pb[now.id]));
        }
        else if(now.is==2)
        {
            add1(getid(b[now.id]-p[now.id]),-1);
            add2(getid(p[now.id]+b[now.id]-1),-1);
        }
    }
    for(int i=1;i<=m;i++)
    {
         printf("%d ",ans[i]);
    }
    return 0;
}