●POJ 1556 The Doors（简单计算几何+最短路）

●赘述题目

10*10的房间内，有竖着的一些墙（不超过18个）。问从点（0，5）到（10，5）的最短路。

按照输入样例，输入的连续5个数,x,y1,y2,y3,y4,表示(x,0--y1),(x,y2--y3),(x,y4--10)是墙壁。

●题解

方法：建图（用到简单计算几何）+最短路

○记录下每个端点。

○包含起点，终点，以及每个墙的可以走的端点，如下图：

○然后枚举点，尝试两两组合连(线段)边，若该线不会撞在墙上，即不会与墙壁线段相交，就add_adge()。

效果图如下：

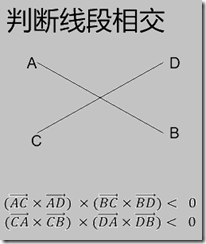
如何判断呢? 计算几何呗。我用的方法如下，须同时满足两个条件：

●代码

#include<cmath>
#include<cstdio>
#include<queue>
#include<cstring>
#include<iostream>
using namespace std;
const double eps=1e-8;
typedef pair<double,int> pii;
struct point{double x,y;}p[105];
struct seg{double x1,y1,x2,y2;}w[105];
struct vec{
	double x,y;
	double operator ^(const vec rtm) {return x*rtm.y-y*rtm.x;} //向量叉乘（模）
	vec operator -(const vec rtm) {return (vec){x-rtm.x,y-rtm.y};}
}v1,v2,v3,v4,v5,v6,v7,v8;
struct edge{
	int to; double co; int next;
}e[10005];
int head[105];
double d[105];
int n,dnt,snt,ent;
double dis(point a,point b) {return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
int sign(double a)
{
	if(fabs(a)<eps) return 0;
	return a>0?1:-1;
}
void add(int u,int v,double c)
{
	e[ent]=(edge){v,c,head[u]};head[u]=ent++;
	e[ent]=(edge){u,c,head[v]};head[v]=ent++;
}
void dijkstra()
{
	for(int i=1;i<=dnt;i++) d[i]=1e7+9;
	priority_queue<pii> q;
	q.push((pii){0,1});d[1]=0;
	while(!q.empty())
	{
		pii u=q.top();q.pop();
		if(d[u.second]<u.first) continue;
		for(int i=head[u.second];i!=-1;i=e[i].next)
		{
			int v=e[i].to;
			if(d[v]>d[u.second]+e[i].co)
			{
				d[v]=d[u.second]+e[i].co;
				q.push((pii){d[v],v});
			}
		}
	}
}
int main()
{
	p[++dnt]=(point){0,5}; p[++dnt]=(point){10,5};
	while(1)
	{
		memset(head,-1,sizeof(head));
		dnt=2;snt=0;ent=0;
		scanf("%d",&n);
		if(n==-1) break;
		double x,y1,y2,y3,y4;
		for(int i=1;i<=n;i++)
		{
			scanf("%f%f%f%f%f",&x,&y1,&y2,&y3,&y4);
			p[++dnt]=(point){x,y1}; p[++dnt]=(point){x,y2}; p[++dnt]=(point){x,y3}; p[++dnt]=(point){x,y4};
			w[++snt]=(seg){x,0,x,y1}; w[++snt]=(seg){x,y2,x,y3}; w[++snt]=(seg){x,y4,x,10};
		}
		bool fg;
		for(int i=1;i<dnt;i++) for(int j=i+1;j<=dnt;j++)
		{
			fg=1;
			for(int k=1;k<=snt;k++)
			{
				v1=(vec){p[i].x-w[k].x1,p[i].y-w[k].y1};
				v2=(vec){p[i].x-w[k].x2,p[i].y-w[k].y2};
				v3=(vec){p[j].x-w[k].x1,p[j].y-w[k].y1};
				v4=(vec){p[j].x-w[k].x2,p[j].y-w[k].y2};	

				v5=(vec){0,0}-v1;
				v6=(vec){0,0}-v3;
				v7=(vec){0,0}-v2;
				v8=(vec){0,0}-v4;
				if(sign((v1^v2)*(v3^v4))<0&&(sign(v5^v6)*(v7^v8))<0) {fg=0;break;}
			}
			if(fg) add(i,j,dis(p[i],p[j]));
		}
		dijkstra();
		printf("%.2f\n",d[2]);
	}
	return 0;
}