【BZOJ 3569】 DZY Loves Chinese II

题目连接：

　　传送门

题解：

　　先%一发大佬的题解。

　　考虑一个图，删除一些边以后不连通的条件为，某个联通块与外界所有连边都被删掉，而不只是生成树中一个树边与所以覆盖它的非树边（很容易举出反例）。

　　那么考虑如何才能判断一个联通块与外界隔断。

　　先考虑只是一棵树，那么任意割一条边都成立，那么现在我们在这棵树上加上一条边(u,v)，我们发现，在(u,v)以外的树边，割一条就成立，但在（u,v）覆盖以内呢？

　　如图：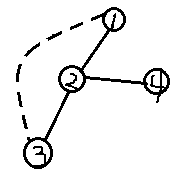　　

　　我们发现我们可以把（u,v）与被（u,v）覆盖的任意一条边删掉，但也可以把2向外连出，且被（u,v）覆盖的边给删掉（即(1,2)、（2，3））。当我们把（2）看作一团点时我们可以发现以上条件也是成立的。

　　以此类推我们可以发现被覆盖的树边删除后不再联通的条件为：1.删除其本身，同时将覆盖其的边删掉；2.删除其本身，将与其一同被覆盖的其他树边删掉。

　　也就是说，产生新联通块的必要条件为：删掉一条树边的同时，与其具有相同属性的边也被删掉。

　　那么这个相同属性是什么：覆盖边的属性。我们用一个数来表示覆盖边的属性，也就是说我们删除的集合要满足删除边的属性异或和为0，同时不能为空集！

　　还是如上图，我们把（1，3）的边用x表示，我们给（2，3）、（1，2），即被覆盖边都打上x的标记，那么我们发现删除这三者中的任意二者都是成立的，因为x这个属性，被gank了两次，也就意味着这个覆盖边的贡献在我们删掉的边之间的联通块（假想块），与覆盖边以外的联通块隔离。

　　所以我们随机一个数给非树边作为它的属性，那么删边形成新联通的条件就是删边集合中，存在一个子集（不含空集）的属性异或和为0。

代码：

 #include "bits/stdc++.h"

 using namespace std;

 inline int read() {
     int s=,k=;char ch=getchar();
     while (ch<''|ch>'') ch=='-'?k=-:,ch=getchar();
     while (ch>&ch<='') s=s*+(ch^),ch=getchar();
     return s*k;
 }

 const int N=5e5+,mod=1e9;

 struct edges{
     int v;edges *last;
 }edge[N*],*head[N];int cnt=;

 inline void push(int u,int v){
     edge[++cnt]=(edges){v,head[u]},head[u]=edge+cnt;
 }

 struct node {
     int x,y,val;
 }ed[N];

 bool vis[N],used[N];int fat[N],val[N];

 inline void dfs(int x,int fa){
     vis[x]=true;
     for (edges *i=head[x];i;i=i->last)  if(i->v!=fa&&!vis[i->v]){
         fat[i->v]=x;used[i-edge>>]=true;
         dfs(i->v,x);
     }
 }

 inline void dfs2(int x,int fa){
     for (edges *i=head[x];i;i=i->last)  if(fat[i->v]==x){
         dfs2(i->v,x);
         val[x]^=val[i->v];
         ed[i-edge>>].val^=val[i->v];
     }
 }

 int n,m,b[],bin[];

 int main() {
     srand();
     n=read(),m=read();
     register int i,j,k;
     for (i=;i<=m;++i)  ed[i].x=read(),ed[i].y=read(),push(ed[i].x,ed[i].y),push(ed[i].y,ed[i].x);
     dfs(,);
     for (i=;i<=m;++i)  if(!used[i]){
         int x=1ll*rand()*rand()%mod+;
         ed[i].val=x;
         val[ed[i].x]^=x;
         val[ed[i].y]^=x;
     }
     dfs2(,);
     int Q=read(),num,x,ans=;
     for (i=;i<=;++i) bin[i]=<<i;
     while (Q--){
         num=read();
         memset(b,,sizeof(b));
         bool flag=true;
         for (i=;i<=num;++i){
             x=read()^ans;x=ed[x].val;
             for (j=;~j;--j)   if(x&bin[j]){
                 if(b[j])    x^=b[j];
                 else    {
                     b[j]=x;
                     for (k=j-;~k;--k)  if(b[k]&&(bin[k]&b[j])) b[j]^=b[k];
                     for (k=j+;j<=;++j)   if(b[k]&bin[j]) b[k]^=b[j];
                     break;
                 }
             }
             if(x==)   flag=false;
         }
         ans+=flag;
         puts(flag?"Connected":"Disconnected");
     }
 }