机器学习：PCA（降噪）

一、噪音

• 噪音产生的因素：可能是测量仪器的误差、也可能是人为误差、或者测试方法有问题等；

• 降噪作用：方便数据的可视化，使用样本特征更清晰；便于算法操作数据；

• 具体操作：从 n 维降到 k 维，再讲降维后的数据集升到 n 维，得到的新的数据集为去燥后的数据集；

• 降维：X_reduction = pca.transform ( X )

• 升维：X_restore = pca.inverse_transform ( X_reduction )，数据集 X_restore 为去燥后的数据集；

二、实例

　1）例一

• 模拟并绘制样本信息

  import numpy as np
  import matplotlib.pyplot as plt
  
  X = np.empty((100, 2))
  X[:, 0] = np.random.uniform(0., 100, size=100)
  X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0, 5, size=100)
  
  plt.scatter(X[:, 0], X[:, 1])
  plt.show()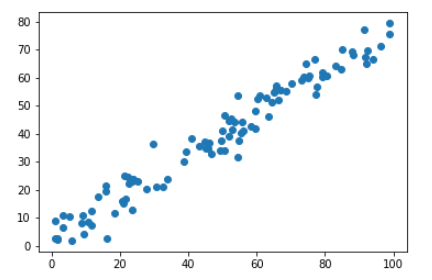

  

1. 实际上，样本的状态看似在直线上下抖动式的分布，其实抖动的距离就是噪音；

• 使用 PCA 降维，达到降噪的效果

1. 操作：数据降维后，再升到原来维度；
2. inverse_transform(低维数据)：将低维数据升为高维数据

3. from sklearn.decomposition import PCA
   
   pca = PCA(n_components=1)
   pca.fit(X)
   X_reduction = pca.transform(X)
   
   # inverse_transform(低维数据)：将低维数据升为高维数据
   X_restore = pca.inverse_transform(X_reduction)
   
   plt.scatter(X_restore[:,0], X_restore[:,1])
   plt.show()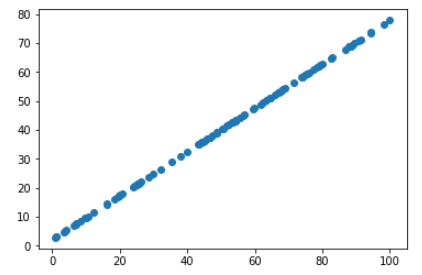

   

　2）例二（手写识别数字数据集）

• 加载数据集（人为加载噪音：noisy_digits）

  from sklearn import datasets
  
  digits = datasets.load_digits()
  X = digits.data
  y = digits.target
  
  # 在数据集 X 的基础上创建一个带噪音的数据集
  noisy_digits = X + np.random.normal(0, 4, size=X.shape)

• 从带有噪音的数据集 noisy_digits 中提出示例数据集  example_digits

  example_digits = noisy_digits[y==0,:][:10]
  for num in range(1, 10):
      X_num = noisy_digits[y==num,:][:10]
      # np.vstack([array1, array2])：将两个矩阵在水平方向相加，增加列数；
      # np.hstack([array1, array2])：将两矩阵垂直相加，增加行数；
      example_digits = np.vstack([example_digits, X_num])
  
  example_digits.shape
  # 输出：（100, 64）

• 绘制示例数据集 example_digits（带噪音）

  def plot_digits(data):
      fig, axes = plt.subplots(10, 10, figsize=(10,10),
                               subplot_kw = {'xticks':[], 'yticks':[]},
                               gridspec_kw=dict(hspace=0.1, wspace=0.1))
      for i, ax in enumerate(axes.flat):
          ax.imshow(data[i].reshape(8, 8),
                   cmap='binary', interpoltion='nearest',
                   clim=(0, 16))
  
      plt.show()
  
  plot_digits(example_digits)

  

• 降噪数据集 example_digits

  # 如果噪音比较多，保留较少信息（此例中只保留 50% 的信息）
  pca = PCA(0.5)
  pca.fit(noisy_digits)
  
  # 查看最终的样本维度
  pca.n_components_
  # 输出：12
  
  # 1）降维：将数据集 example_digits 降维，得到数据集 components
  components = pca.transform(example_digits)
  
  # 2）升维：将数据集升到原来维度（100, 64）
  filtered_digits = pca.inverse_transform(components)
  
  # 绘制去燥后的数据集 filtered_digits
  plot_digits(filtered_digits)