POJ3417Network

Network

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 5311		Accepted: 1523

Description

Yixght is a manager of the company called SzqNetwork(SN). Now she's very worried because she has just received a bad news which denotes that DxtNetwork(DN), the SN's business rival, intents to attack the network of SN. More unfortunately, the original network of SN is so weak that we can just treat it as a tree. Formally, there are N nodes in SN's network, N-1 bidirectional channels to connect the nodes, and there always exists a route from any node to another. In order to protect the network from the attack, Yixght builds M new bidirectional channels between some of the nodes.

As the DN's best hacker, you can exactly destory two channels, one in the original network and the other among the M new channels. Now your higher-up wants to know how many ways you can divide the network of SN into at least two parts.

Input

The first line of the input file contains two integers: N (1 ≤ N ≤ 100 000), M (1 ≤ M ≤ 100 000) — the number of the nodes and the number of the new channels.

Following N-1 lines represent the channels in the original network of SN, each pair (a,b) denote that there is a channel between node a and node b.

Following M lines represent the new channels in the network, each pair (a,b) denote that a new channel between node a and node b is added to the network of SN.

Output

Output a single integer — the number of ways to divide the network into at least two parts.

Sample Input

4 1
1 2
2 3
1 4
3 4

Sample Output

3

Source

POJ Monthly--2007.10.06, Yang Mu

 

题目大意：对于一棵树，加上m条非树边。每次只能删一条树边和一条非树边使图不连通有多少种方法 。

题解：LCA+树上差分

首先可以想到的暴力为两重for循环枚举删的树边与非树边，然后bfs判断图是否联通。

然后我们可以优化一下，枚举树边，讨论删掉当前枚举的树边，和多少条非树边图能不连通。

分类讨论。

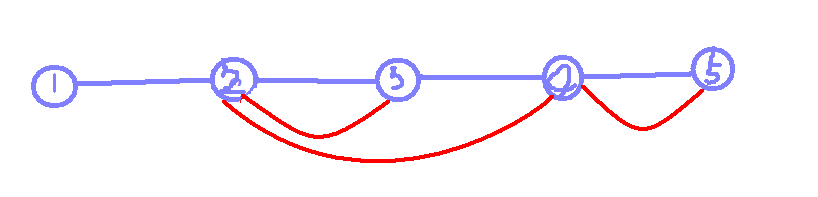
从链的情况开始，红色的边为非树边。首先看1--2这条边，没有任何非树边覆盖，所以要删这条边，

你删任何一条树边都可以，所以这条边对答案的贡献是m。再看4--5这条边，被一条非树边覆盖，如果

删去这条边并且再删去一条非树边，想要使图不连通，只能删覆盖它的非树边，所以当只有一条非树边

覆盖这条边时，这条边对答案的贡献是1。再看2--3这条边，如果删去这条边,想要使图不连通，你删哪条

非树边都是没有用的，图仍会连通。对答案产生贡献的树边的条件是，如果没有被非树边覆盖，产生的

贡献是m，如果被一条非树边覆盖，产生的贡献就是1，即删掉覆盖它的非树边，如果被2及其以上的非树

边覆盖,对答案没有贡献，你删那一条非树边图仍然连通。

好了，我们已经讨论完答案的产生，在说明怎样实现。

进行树上差分来实现每一条树边被几条非树边覆盖。

当一条非树边的端点为u,v时，查分数组dp[u]++,dp[v]++,dp[lca(u,v)]-=2.

然后在dfs一遍求差分数组的后缀和，dp[i]表示i和它父亲相连的这条边被几条非树边覆盖。

最后统计答案即可。

1A好开心~=u=//

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 100002
using namespace std;
 
int n,m,sumedge,ans;
int head[maxn],top[maxn],deep[maxn],dad[maxn],size[maxn],dp[maxn];
 
struct Edge{
    int x,y,nxt;
    Edge(int x=,int y=,int nxt=):
        x(x),y(y),nxt(nxt){}
}edge[maxn<<];
 
void add(int x,int y){
    edge[++sumedge]=Edge(x,y,head[x]);
    head[x]=sumedge;
}
 
void dfs(int x){
    size[x]=;deep[x]=deep[dad[x]]+;
    for(int i=head[x];i;i=edge[i].nxt){
        int v=edge[i].y;
        if(v==dad[x])continue;
        dad[v]=x;
        dfs(v);
        size[x]+=size[v];
    }
}
 
void dfs_(int x){
    int s=;
    if(!top[x])top[x]=x;
    for(int i=head[x];i;i=edge[i].nxt){
        int v=edge[i].y;
        if(v!=dad[x]&&size[v]>size[s])s=v;
    }
    if(s){
        top[s]=top[x];
        dfs_(s);
    }
    for(int i=head[x];i;i=edge[i].nxt){
        int v=edge[i].y;
        if(v!=dad[x]&&v!=s)dfs_(v);
    }
}
 
int lca(int x,int y){
    for(;top[x]!=top[y];){
        if(deep[top[x]]>deep[top[y]])swap(x,y);
        y=dad[top[y]];
    }
    if(deep[x]>deep[y])swap(x,y);
    return x;
}
 
void DP(int x){
    for(int i=head[x];i;i=edge[i].nxt){
        int  v=edge[i].y;
        if(v==dad[x])continue;
        DP(v);
        dp[x]+=dp[v];
    }
}
 
int main(){
    scanf("%d%d",&n,&m);
    for(int i=;i<n;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
    }
    dfs();dfs_();
    for(int i=;i<=m;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        dp[x]++;dp[y]++;
        dp[lca(x,y)]-=;
    }
    DP();
    for(int i=;i<=n;i++){
        if(dp[i]==)ans+=m;
        else if(dp[i]==)ans++;
        //cout<<dp[i]<<endl;
    }
    cout<<ans<<endl;
    return ;
}