安全狗两个中危提权+NET提权

1.循环加组复现

for /l %%i in (1,1,1000) do @net user admin admin /add&@ net localgroup administrators admin /add

这曾经是安全狗最早爆出的安全狗漏洞

但是安全狗很快的在之后的版本修复了

上月某非盈利安全研究小组研究人员发现其实安全狗只是阻截了系统的net/net1执行  同时把你net放到别的目录就算有执行权限你也无法执行  因为他是一棒子打死  但是可以突破执行net1   (没图说个jb)

正常情况下执行net是被禁止的

尝试在别的目录也是被禁止的

峰回路转的前提下我们想到了net1

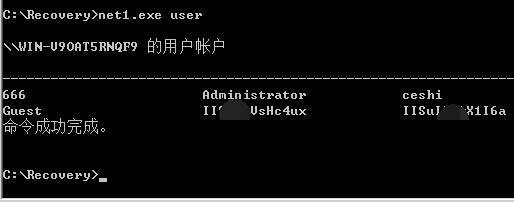
嗯  到这net已经突破执行了   那要怎么提权呢？

看图说话

这里大家肯定会说安全狗不是修复了么···

继续往下看

这里我加的账户是 admin

和之前一样  除了间隔2秒删除账户之外  其他一点没变

至此  突破安全狗账户守护提权成功

———————————————————————————————————————————————-

2.杀狗提权（鸡肋）

其实这也是一个新思路   安全狗的一切都是以进程的方式展现运行的  之前有很多的k狗神器   他的目的就是终止或者杀死安全狗的守护进程  让安全狗保护失效  但是在后期安全狗把此问题修复了

但是什么都是可以被突破的   上月同样的发现了安全狗的这个问题

安全狗守护进程没有采用特别的保护  只要有一定的权限  就可以实现拒绝服务(没图我说个jb啊)

安全狗的守护进程路径在C:\Program Files\SafeDog\SafedogServer\SafeDogGuardCenter\

我们只需要让他这个下面的SafeDogGuardCenter.exe加载不起来就行了  具体怎么做呢1条命令搞定:

cacls “C:\Program Files\SafeDog\SafedogServer\SafeDogGuardCenter\SafeDogGuardCenter.exe” /t /e /c /d system

这条命令的意思是拒绝System读取+运行这个程序SafeDogGuardCenter.exe

System都没权限读取了  他怎么运行呢 (没图我tmd说个jb啊)

我们继续

至此  杀狗结束  想干吗就干嘛去吧

(ps:此方法鸡肋的地方在于需要重启对方的服务器)

后记：都已经是System权限了  还提权做什么  脑子进水了么

———————————————————————————————————————————————-

3.NET提权细节以及防御措施

尊重原文作者  不剽窃他人创意   我们在这里只谈如何修复这类漏洞

http://www.wooyun.org/bugs/wooyun-2010-0104148

这个是发现.NET提权漏洞的原文作者

利用条件有三条：

1.需要支持aspx并且高于Microsoft .NET Framework 1.14版本

2.安全模式除外（现在还没有能突破.net安全模式的方法）

3.必须要网站根目录拥有全部可写权限（更改）权限

没图我说个jb  直接上图

首先让我们的网站运行于独立权限账户test下面

画红圈的地方  就是NET提权漏洞的玄机  我们继续往下分析

嗯  可以看到菜刀已经备好了

执行这个作者的EXP

我们在他的网站目录放一个cmd.exe

然后去执行   我贴出关键的提权代码

var strPath:String = “D:\\2222222\\333333333\\cmd.exe”, strUser:String = “everyone”;

大概意思就是授予everyone去操作CMD的命令  真实情况是不是这样呢  我们执行一下

嗯  大家是不是感觉到神奇的样子

没错  他的玄机就在于你给了他网站更改权限

我们去掉更改权限之后  继续实验

所以说这个从严格意义来讲  不能算是NET框架的漏洞  只是算是windows中的一个权限问题