ArrayList源码深度解析

jdk：1.8

一、先看看ArrayList类的整体概述，

　　　　ArraList是基于动态数组实现的一种线性列表，这种基于动态数组的好处就是索引比较快，时间复杂度为O(1)；但是对数据修改比较慢，因为需要移动数据，移动数据的过程需要消耗大量的时间

　　　　因此我们在平时的使用的过程中，需要结合我们的具体业务需求来决定到底应不应该使用ArrayList，如果你只是需要保存数据然后进行查找，这种情况就适合使用ArrayList，如果需要大量的修改，增加或者删除时，这时就不要使用ArrayList

1. 先看ArrayList的继承结构，如下图

　　　　在Idea中使用Ctrl+H快捷键可以快速查看类的继承结构，不过这是能查看父类（不可以查看父接口）

　　　　

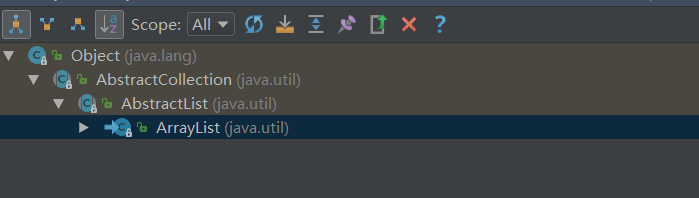
　　　　　　在idea中也可以查看类的UML图，如下

　　　　

　　2.下面两张图是ArrayList类的方法列表，其中绿色的打开的锁表示公共方法，红色的关闭的锁表示私有方法，钥匙形状的图表表示受保护的方法

　　　　

　　　　

二、详细介绍

• 主要变量

　　

• 主要方法
  • 构造方法

　　

　　public ArrayList(int initialCapacity)构造方法：该方法带一个整型参数，用该参数可以指定列表的初始容量

　　public ArrayList()构造方法：

　　public ArrayList(Collection<? extends E> c)构造方法：用一个一直的集合去初始化一个数组元素

• • 主要对方法

　　　　　　public boolean add(E e)：向ArrayList中添加一个元素（直接追加到数组的末尾），本质就是向动态数组中添加了一个元素，不过这里并不是简单的直接添加元素，在添加之前需要对数据进行容量检查，确保是否有足够的空间来存放待添加的元素（检查的过程即是调用rangeCheck函数，
　　　　　　　　当发现空间不足时，会调用ensureCapacityInternal来动态分配空间）

　　　　　　public void add(int index, E element)：向数组中指定的位置添加元素，和add(E e)除了添加的位置不同，其他完全一致

　　　　　　public E set(int index, E element)

　　　　　　public E remove(int index)

　　　　　　public boolean remove(Object o)

　　　　　　public void clear()

　　　　　　private void rangeCheck(int index)

　　　　　　private void ensureCapacityInternal(int minCapacity)：该函数是数组动态扩容的入口函数，
　　　　　　　　调用链如下

　　　　　　　　

　　　　　　　　动态扩容的基本思路：

• • • • 计算出当前数组的大小，以当前的大小的1.5倍（即上图中的newCapacity）作为扩容后的大小
      • 判断newCapacity和传入的最小容量需求minCapacity，如果newCapacity<minCapacity，这直接把minCapacity赋值给newCapacity
      • 检查赋值后的newCapacity是否超过int的最大值（这里用是否小于0来判断是否溢出，溢出直接抛出异常），否则在int的最大值和MAX_ARRAY_SIZE中取较小的值作为最终的newCapacity
      • 调用Arrays.copyOf方法，把原始数据复制到扩容的数组，经过以上步骤后，数组的

　　　　　　private void ensureExplicitCapacity(int minCapacity)：和int的最大值以及数据默认的最大容量比较，得出最终的扩容容量

　　　　　　private void grow(int minCapacity)：该方法是在确定了扩容后的数组大小后，真正执行扩容的步骤

总结：在对ArrayList进行操作的时候都会去判断是否越界，即执行rangeCheck方法，以及在向ArrayList中插入数据时判断是否需要扩容