一些推导的笔记

上面分解成无穷维，大多数时候都不是的吧。。。

这里的d有限维，应该是指相对小于上面的分解的维度的某个数

参考资料

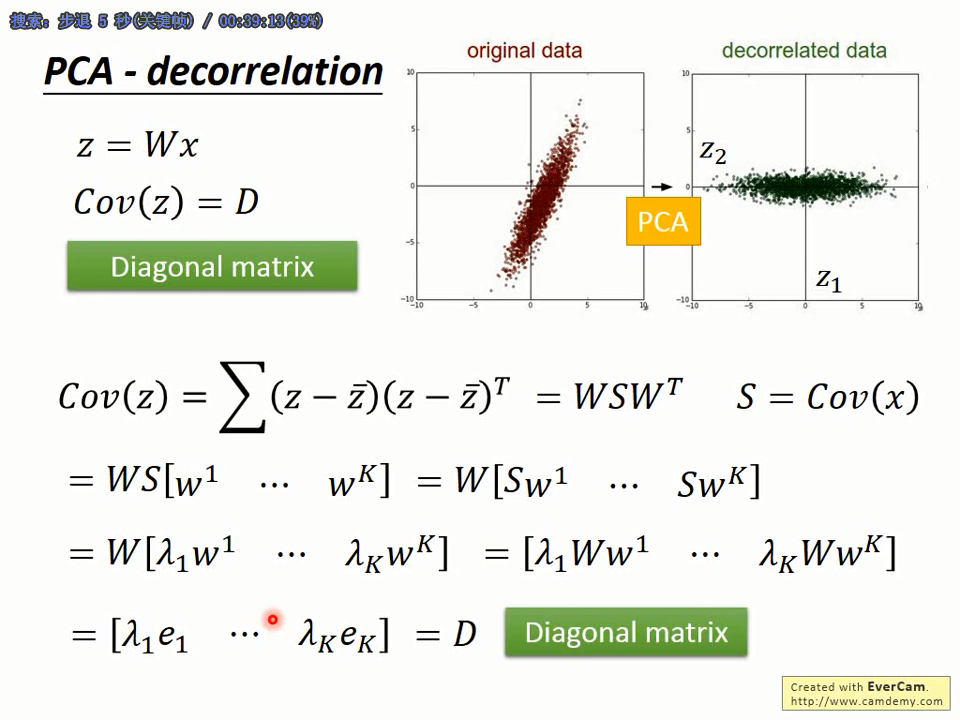
参考资料，上面是从最小化损失的角度，利用拉格朗日对偶的优化方法求解

pca的另一种最大化方差的解释

kl变换和pca区别

KL变换和PCA的数学推导的更多相关文章

  1. 主成分分析（PCA）算法，K-L变换 角度

    主成分分析(PCA)是多元统计分析中用来分析数据的一种方法,它是用一种较少数 量的特征对样本进行描述以达到降低特征空间维数的方法,它的本质实际上是K-L变换.PCA方法最著名的应用应该是在人脸识别中特 ...

  2. K-L变换和 主成分分析PCA

    一.K-L变换 说PCA的话,必须先介绍一下K-L变换了. K-L变换是Karhunen-Loeve变换的简称,是一种特殊的正交变换.它是建立在统计特性基础上的一种变换,有的文献也称其为霍特林(Hot ...

  3. PCA的数学原理

    PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维 数据的 ...

  4. PCA的数学原理(转)

    PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降 ...

  5. Maths | 离散K-L变换/ 主成分分析法

    目录 1. 概述 2. K-L变换方法和原理推导 2.1. 向量分解 2.2. 向量估计及其误差 2.3. 寻找最小误差对应的正交向量系 3. K-L变换高效率的本质 4. PCA在编.解码应用上的进 ...

  6. UVA - 10014 - Simple calculations （经典的数学推导题！！）

    UVA - 10014 Simple calculations Time Limit: 3000MS Memory Limit: Unknown 64bit IO Format: %lld & ...

  7. 统计知识选讲（二）——主成分分析（PCA）的推导和应用

    1.数学推导 根据上讲的思想,我们可以用下图来进行数学上的推导. 2.PCA的步骤 1)对原始数据进行标准化处理:对该指标变量进行标准化, 2)计算相关系数矩阵(协方差矩阵) 3)计算相关系数矩阵的特 ...

  8. LDA-线性判别分析（二）Two-classes 情形的数学推导

    本来是要调研 Latent Dirichlet Allocation 的那个 LDA 的, 没想到查到很多关于 Linear Discriminant Analysis 这个 LDA 的资料.初步看了 ...

  9. 借One-Class-SVM回顾SMO在SVM中的数学推导--记录毕业论文5

    上篇记录了一些决策树算法,这篇是借OC-SVM填回SMO在SVM中的数学推导这个坑. 参考文献: http://research.microsoft.com/pubs/69644/tr-98-14.p ...

随机推荐

  1. Set Matrix Zeroes——常数空间内完成

    Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in place. Did yo ...

  2. Apache配置基于端口号的虚拟主机 Apache virtual host configuration is based on the port

    有可能只有一个ip出口,但却有多个项目,那么就需要基于端口号架设虚拟主机. Step 1: 检查是否开启 httpd-vhosts.conf apache/conf/httpd.conf文件 # Vi ...

  3. Linux下cp命令的使用说明

    [root@www ~]# cp [-adfilprsu] 来源档(source) 目标档(destination)[root@www ~]# cp [options] source1 source2 ...

  4. 【转载】Web Service 的工作原理

    http://www.cnblogs.com/Jessy/p/3528341.html Web Service基本概念 Web Service也叫XML Web Service WebService是 ...

  5. Vue.js—组件快速入门及Vue路由实例应用

    上次我们学习了Vue.js的基础,并且通过综合的小实例进一步的熟悉了Vue.js的基础应用.今天我们就继续讲讲Vue.js的组件,更加深入的了解Vue,js的使用.首先我们先了解一下什么是Vue.js ...

  6. Jenkins+maven+Tomcat配置发布

    jenkins大多数情况下都是用来部署Java项目,Java项目有一个特点是需要编译和打包的,一般情况下编译和打包都是用maven完成,所以系统环境中需要安装maven. 实验环境: 10.0.0.1 ...

  7. POJ 3259 Wormholes【最短路/SPFA判断负环模板】

    农夫约翰在探索他的许多农场,发现了一些惊人的虫洞.虫洞是很奇特的,因为它是一个单向通道,可让你进入虫洞的前达到目的地!他的N(1≤N≤500)个农场被编号为1..N,之间有M(1≤M≤2500)条路径 ...

  8. 解决Linux环境下安装xampp之后外部无法连接MySQL的问题

    在Linux系统下,开发PHP一般都是LAMP环境,对于开发环境来讲,没有必要花太大精力去单独配置LAMP环境,采用xampp一键安装包是一个很好的方式.在Linux系统上安装xampp的过程这里就不 ...

  9. 【大视野入门OJ】1083：数组的二分查找

    Description 在1500个整数中查整数x的位置,这些数已经从小到大排序了.若存在则输出其位置,若不存在则输出-1. Input 第一行,一个整数x 后面1500行,每行一个整数 Output ...

  10. WebForms UnobtrusiveValidationMode 需要“jquery”ScriptResourceMapping——牛腩新闻发布系统

    VS2011使用验证控件出现" WebForms UnobtrusiveValidationMode 需要"jquery"ScriptResourceMapping.请添 ...