【[USACO15JAN]草鉴定Grass Cownoisseur】

这大概是我写过的除了树剖以外最长的代码了吧

首先看到有向图和重复经过等敏感词应该能想到先tarjan后缩点了吧

首先有一个naive的想法，既然我们要求只能走一次返回原点，那我们就正着反着建两遍图，分别处理出1到其他点的所能经过的最多点数和其他点到1经过的最大点数，之后找到那些和1有正边或反边相连的点，之后逆行这一条边，取一个max就好了

于是洋洋洒洒写了100多行发现连样例都过不了

本着交一交试试看的心态交了上去，发现还能过四个点

于是就去手画了一遍样例，发现自己真的是非常naive

样例是这个样子的

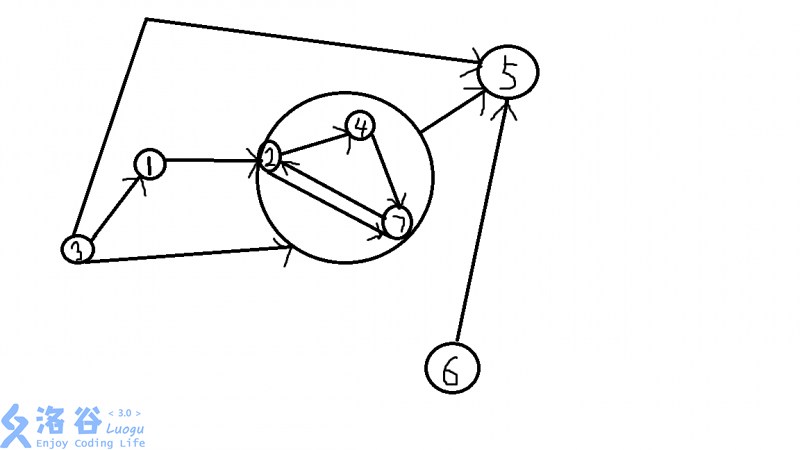
尽管很丑，但就勉强看看吧

我们发现按照刚才那个思路我们显然是要挂的

因为按照那样跑出来的结果是4，但这里的最佳方案应该是从1到那个缩好的点再到5，之后逆行一次走到3，之后走回1

这样我们如果只考虑能到到1的或只考虑能被1到达的，显然是不行的

这样不行怎么办，我们放到一起考虑就好了

如果一个能被1到达的点（比如说样例里的5）有一条边（当然这是一条反边）能到达一个能到达1的点，我们就可以把这两种情况一起考虑

同理一个能到达1的点有一条边（自然这是一条正边）和一个能被1到达的点相连，这两种情况也可以一起考虑

所以就是代码了

#include<iostream>
#include<cstring>
#include<cstdio>
#include<bitset>
#define re register
#define maxn 100001
using namespace std;
struct node
{
	int v,nxt;
}e[maxn],e1[maxn],e2[maxn];
int head[maxn],head1[maxn],head2[maxn];
int dfn[maxn],low[maxn],st[maxn],belong[maxn],dp1[maxn],d[maxn],dp2[maxn];
int f1[maxn],f2[maxn];
int q[maxn],r[maxn],c[maxn];
bitset<maxn> f;//闲的没事干开了bitset
int n,m,top,k,p,num,num1,num2,mid;
inline void add_edge(int x,int y)
{
	e[++num].v=y;
	e[num].nxt=head[x];
	head[x]=num;
}//原图
inline void add_edge_1(int x,int y)
{
	e1[++num1].v=y;
	e1[num1].nxt=head1[x];
	head1[x]=num1;
}//缩点后新图建正边
inline void add_edge_2(int x,int y)
{
	e2[++num2].v=y;
	e2[num2].nxt=head2[x];
	head2[x]=num2;
}//缩点后新图建反边
inline int read()
{
	char c=getchar();
	int x=0;
	while(c<'0'||c>'9') c=getchar();
	while(c>='0'&&c<='9')
	  x=(x<<3)+(x<<1)+c-48,c=getchar();
	return x;
}
void tarjan(int x)
{
	dfn[x]=low[x]=++k;
	f[x]=1;
	st[++top]=x;
	for(re int i=head[x];i;i=e[i].nxt)
	if(!dfn[e[i].v]) tarjan(e[i].v),low[x]=min(low[x],low[e[i].v]);
	else if(f[e[i].v]) low[x]=min(low[x],dfn[e[i].v]);
	if(dfn[x]==low[x])
	{
		p++;
		do
		{
			mid=st[top--];
			f[mid]=0;
			d[p]++;//记录新点点权
			belong[mid]=p;//记录好每一个点属于哪一个缩完点后的新点
		}while(x!=mid);
	}
}
int main()
{
	n=read();
	m=read();
	int x,y;
	for(re int i=1;i<=m;i++)
	{
		x=read();
		y=read();
		add_edge(x,y);
	}
	for(re int i=1;i<=n;i++)
	if(!dfn[i]) tarjan(i);//缩点！
	for(re int i=1;i<=n;i++)
	for(re int j=head[i];j;j=e[j].nxt)
	if(belong[i]!=belong[e[j].v])
	{
		r[belong[e[j].v]]++,add_edge_1(belong[i],belong[e[j].v]);//建正图
		c[belong[i]]++,add_edge_2(belong[e[j].v],belong[i]);//建反图
	}
	f[belong[1]]=1;//我们开一个标记数组,标记那些点可以被1到达,拓扑排序的时候只有这些点才进行动规,其余的点只做删边操作
	dp1[belong[1]]=d[belong[1]];
	int tot=0;
	for(re int i=1;i<=p;i++)
	if(!r[i]) q[++tot]=i;
	for(re int i=1;i<=tot;i++)
	{
		for(re int j=head1[q[i]];j;j=e1[j].nxt)
		{
			r[e1[j].v]--;
			if(f[q[i]])
			{
				f[e1[j].v]=1;
				dp1[e1[j].v]=max(dp1[e1[j].v],dp1[q[i]]+d[e1[j].v]);
                //dp1[i]表示从1到i形成的最大点权
			}
			if(!r[e1[j].v]) q[++tot]=e1[j].v;
		}
	}
	int ans=0;
	for(re int i=head1[belong[1]];i;i=e1[i].nxt)
		ans=max(ans,dp1[e1[i].v]);
	for(re int i=1;i<=p;i++)
		f1[i]=f[i];//记录那些点可以被1到达
	tot=0;
	memset(q,0,sizeof(q));
	f.reset();//bitset清零
	f[belong[1]]=1;//标记同理，表示这个点可以到达1
	dp2[belong[1]]=d[belong[1]];
	for(re int i=1;i<=p;i++)
	if(!c[i]) q[++tot]=i;
	for(re int i=1;i<=tot;i++)
	{
		for(re int j=head2[q[i]];j;j=e2[j].nxt)
		{
			c[e2[j].v]--;
			if(f[q[i]])
			{
				f[e2[j].v]=1;
				dp2[e2[j].v]=max(dp2[e2[j].v],dp2[q[i]]+d[e2[j].v]);
                //dp2[i]表示i这个点到1形成的最大点权
			}
			if(!c[e2[j].v]) q[++tot]=e2[j].v;
		}
	}
	for(re int i=head2[belong[1]];i;i=e2[i].nxt)
		ans=max(ans,dp2[e2[i].v]);
	for(re int i=1;i<=p;i++)
		f2[i]=f[i];//记录那些点可以到达1
	for(re int i=1;i<=p;i++)
	if(f1[i])//这个点可以被1到达
	{
		for(re int j=head2[i];j;j=e2[j].nxt)//逆行一次
		if(f2[e2[j].v]) ans=max(ans,dp1[i]+dp2[e2[j].v]-d[belong[1]]);//由于两次dp都把1所在的强联通分量的点权算了进去，所以要减去一个1所在的强联通分量的点权
	}
	for(re int i=1;i<=p;i++)
	if(f2[i])
	{
		for(re int j=head1[i];j;j=e1[j].nxt)
		if(f1[e1[j].v]) ans=max(ans,dp2[i]+dp1[e1[j].v]-d[belong[1]]);
	}//同理
	ans=max(d[belong[1]],ans);//如果一谁都到达不了，谁也到不了，那么答案就是1的点权了
	printf("%d",ans);
	return 0;
}