【常见加密方法】Base64编码&Tea算法简介

Base64编码

【Base64编码是什么】

　　Base64是一种基于64个可打印字符来表示二进制数据的表示方法。

——维基百科

　　Base64，顾名思义，是基于64种可视字符的编码方式。这64种符号由A-Z,a-z,0-9以及另外两个视不同系统而定的可视自符（一般为+和/）组成。因为六位二进制数可以表示所有1-2⁶以内的整数，所以在编码过程中取每六位二进制数依照顺序对应相应可视字符。

　　Base64将3字节的二进制数据，以先来的字节占据高位，不足三字节则在数据尾部用0补足的规则放入24位缓存器中；在计算时，依次取出6bits进行相应对照编码。而当不足三字节进行补0时，编码结束后要在尾部加上相应补充字节数数量的“=”。

【Base64编码图解】

这里拿RED举个例子：　　

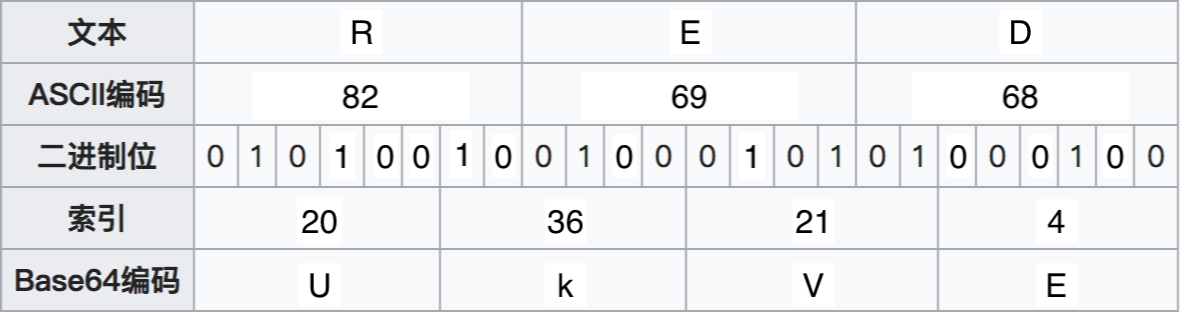
由图中一层层推到而出RED的Base64编码为UkVE

我们再看看维基百科上缺字节进行补0的例子：

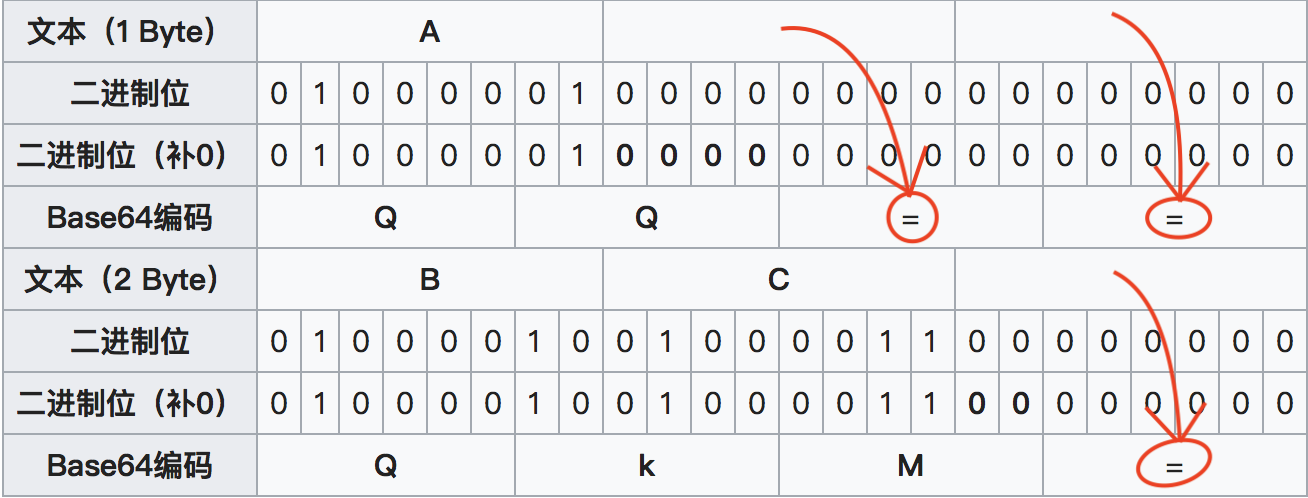
等号数量等于补充的字节数

Tea 算法

【Tea算法是什么】

在密码学中，微型加密算法（Tiny Encryption Algorithm，TEA）是一种易于描述和执行的块密码，通常只需要很少的代码就可实现。

——维基百科

　　Tea算法能够利用4个32位密钥对2个32位明文数据进行多轮加密，利用不断增加的Delta值和两个32位数据相互加密来保持每一轮加密的和其他任何一轮加密不同。在知道4个32位密钥的情况下，利用可逆的加减操作进行数据的加密与解密。

【Tea算法模版与浅析】

这里我用{1234,4321}作为待加密的两个32位明文数据，用{2147483647,2147483646,2147483645,2147483644}作为四个32位密钥举例。

 #include <cstdio>

 const int delta = 0x9e3779b9;//Tea算法作者的建议值
 int scr[],key[];

 void _pre(){
     scr[] = ;
     scr[] = ;
     key[] = ;
     key[] = ;
     key[] = ;
     key[] = ;
 }

 void DoTea(){
     int a = scr[],b = scr[],sum = ;
     for(int i=;i<=;++i){//进行32次迭代加密，Tea算法作者的建议迭代次数
         sum += delta;//不断增加Delta的值
         a += ((b << ) + key[]) ^ (b + sum) ^ ((b >> ) + key[]);//利用多次双位移和异或将明文与密钥扩散混乱，并将两个明文互相加密
         b += ((a << ) + key[]) ^ (a + sum) ^ ((a >> ) + key[]);
     }
     scr[] = a;//将原数据覆盖为密文
     scr[] = b;//将原数据覆盖为密文
     printf("%d %d\n",scr[],scr[]);
 }

 void UndoTea(){//利用可逆性将加密过程逆转
     int a = scr[],b = scr[],sum = 0xc6ef3720;//32次迭代后delta的值
     for(int i=;i<=;++i){
         b -= ((a << ) + key[]) ^ (a + sum) ^ ((a >> ) + key[]);
         a -= ((b << ) + key[]) ^ (b + sum) ^ ((b >> ) + key[]);
         sum -= delta;
     }
     scr[] = a;
     scr[] = b;
     printf("%d %d\n",scr[],scr[]);
 }

 int main(){
     _pre();
     DoTea();
     UndoTea();
     return ;
 }

　　Tea算法的作者建议加密迭代次数为32次*，以保证数据被充分加密；Delta的值本是可以任何数字，但作者为了避免可能的错误而将delta的值建议为delta = (√5 - 1) * 2147483648 ≈ 2654435769.497230296477，取整为2654435769，即0X9e3779b9。

　　Tea算法利用迭代过程中多次的位运算和异或使明文与密钥充分扩散混乱，并以下图方式进行两个数据间的互相加密:

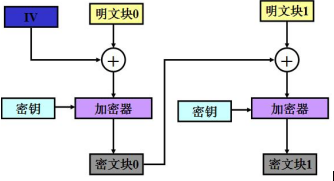
图源自：https://blog.csdn.net/jinzhichaoshuiping/article/details/54588003

　　*注：Tea算法作者强调迭代次数16次即可达到加密效果，但仍然建议32次迭代保证加密牢靠。