详细且透彻的分析PCA原理

前两天面试问到了PCA，感觉讲得不是很透彻，这里再次详细写一下。

首先定义如下变量的含义：

　　X：R^n*m，n个样本m个属性，对于第i个样本xi：R^1*m。

　　W：R^m*k，k个正交的单位正交的列向量组成的矩阵，投影矩阵，把原来的m维降到k维。对于第i个维度wi：R^m*1。

　　投影后的样本矩阵X' = X×W：R^n*k，对于投影后的第i个样本xi' = xi×W：R^1*k。

我们做PCA的目的是找出一个投影矩阵W（也就是k个单位向量）使得样本投影后的方差最大。其实理解了加粗的这句话，就已经对PCA有相当的了解了。如何理解方差最大？答：方差大说明投影后的样本之间相互分离程度比较好，相比于较小的方差，原样本的特征得到了有效保存。这个方差从数学上表示为投影到各个维度的方差之和。

记住，作PCA之前要做的一件事是对原始样本矩阵X，按列中心化。比如对 Xij ==> Xij-M(j)，其中M(j)表示第j列（也就是第j种属性）的均值。为什么要这么做？这是因为这个操作使得X每一列均值为0，可以大大简化后面计算方差的公式。（D(a)=E( (a-avg(a))·(a-avg(a)) )，如果avg(a)=0，那么D(a)=E(a^2)）

对投影后的矩阵X' = X×W，因为X被我们按列中心化了，即∑xi=0，那么∑xi' = ∑ (xi×W) = (∑xi)×W = 0，也就是说投影后列均值为0的性质依然得到了保持。

接下来，我们考虑要优化的目标，方差。先考虑将所有样本投影到单个维度wi的情况，即X×wi：R^n*1，他表示这n个样本分别在这一个维度的坐标。

根据上面的分析，有∑ (xi×wi)=0，即E(X*wi)=0，（注意此处要把wi看成是定值）。于是就有了下面的推算：

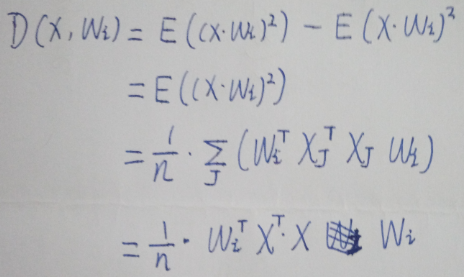
对所有投影方向的方差进行求和，加上原来每个投影向量长度为1的约束，就得到了我们下面的优化问题。

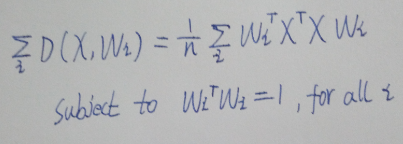
由于是等式约束，我们很容易就可以写成拉格朗日形式如下，（λ前面漏掉了求和符号，sorry）

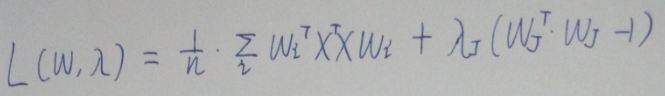
是的对wi求导，得到如下（由于λ是拉格朗日乘子，本身它的乘数不需要关心）

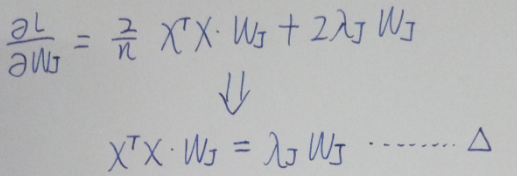
显然，△等式的wj和λ的解就是X^TX做特征值分解对应的特征向量和特征值。

那么，有了特征值分解后，我们应该选哪些特征向量及其对应的特征值呢？ 都知道是从最大的开始选，为什么呢？

对△等式进行简单变化，等式两边同时左乘wjT，变成下面的等式，

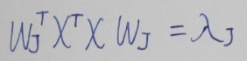
注意到，该等式说明了特征值λj对应的就是wj方向投影的方差，而我们的目标是要最大化所有的方差和。可选的范围是固定，显然我们从大的特征值开始选就行了。这就从数学上解释了为什么我们要从大的特征值开始进行选择（面试的时候问到了，当时只进行感性上的解释，确实没有这样列出来有说服力）。

还有一个trick要注意的是，如果给出了低维空间中的坐标，要复原在原空间的坐标时，要对每一个维度加上对应的均值，这是因为在做PCA之前进行了中心化处理。

怎么样？ 是不是与书籍上的写法不一样呢？