整数的故事(4)——Karastuba算法

　　我们在小学就学过用竖式计算两个多位数的乘法：

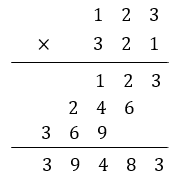
　　这个过程简单而繁琐，没有最强大脑的普通大众通常是用计算器代替的。然而对于超大整数的乘法，计算器也未必靠得住，它还存在“溢出”一说。这就需要我们自行编写算法了。

竖式算法

　　虽然对于Python来说，不必太过关心整数的长度和溢出问题，但对于其它编程语言就未必了。这里我们暂且抛开语言本身的特性，只关注算法本身。假设输入的两个长整数x和y，它们的乘积将会溢出，所以需要将乘积转换成字符串，根据乘法竖式的运算规则，很容易写出下面的代码：

 # 竖式法计算两个整数相乘
 def multi(x, y):
     x_str = str(x)
     y_str = str(y)
     x_len = len(x_str)
     y_len = len(y_str)
     z = [0] * (x_len + y_len)

     for i in range(x_len):
         for j in range(y_len):
             z[x_len - i - 1 + y_len - j - 1] += int(x_str[i]) * int(y_str[j])

     for i in range(len(z) - 1):
         if z[i] >= 10:
             z[i + 1] += (int(z[i]) // 10)
             z[i] = int(z[i]) % 10

     return list2str(z)

 # 将z转换成字符串并删除左侧的0
 def list2str(z):
     result = [str(i) for i in z]
     return ''.join(result[::-1]).lstrip('')

 # 打印运行结果
 def paint(a, b):
     print('{0} * {1} = {2}'.format(a, b, multi(a, b)))

 if __name__ == '__main__':
     paint(123,321)
     paint(123,456)
     paint(123456789000, 987654321000)

　　代码中9~11行用两个循环模拟了乘法计算的过程，以123×321为例，在循环结束后z将存储下面的数据：

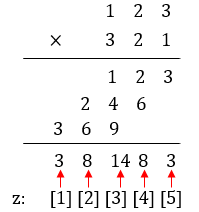
　　11行的for循环是处理进位问题。最后将列表转换为字符串，再去掉多余的0，打印结果：

Karastuba算法

　　竖式乘法偏向于使用蛮力，Karastuba博士在1960年提出了一个更简单的算法，其思想是把两个大整数的乘法转化为若干次小规模的乘法和少量的加法，这就是Karastuba算法。

　　对于两个n位的大整数x和y，可以把x和y分解成两部分：

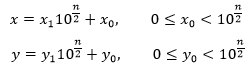
　　例如：

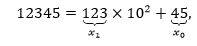
　　是不是有点似成相识？没错，这实际上是利用了欧几里德算式将一个整数分解成m=qn+r的形式。现在x和y的乘积可以表示为：

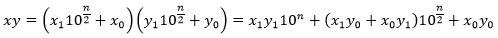
　　这就把原来的大整数乘法变成了四次效较小规模的乘法（其中10ⁿ的运算可以通过位移高效处理）和少量加法。上式还可以更进一步：

　　看起来更复杂了，但是对于计算机来说，x₁y₁和x₀y₀已经计算过了，不需要再次计算。x₁y₀+x₀y₁被转换成一次乘法和少量的加法，多一个加法运算对时间复杂度没有影响，而减少一个乘法却能减少时间复杂度。对每一个乘法都进行类似的分解，反复迭代x_iy_i，直到其中一个乘数只有1位为止。按照这种思路可以编写新的乘法运算代码：

 # karastuba算法计算两个n位的大整数乘法, x >=0, y >= 0
 def karastuba(x, y, n):
     if x == 0 or y == 0:
         return 0
     elif n == 1:
         return x * y

     k = n // 2
     x1 = x // (10 ** k)
     x0 = x % (10 ** k)
     y1 = y // (10 ** k)
     y0 = y % (10 ** k)
     z0 = karastuba(x0, y0, k)         # 计算x0y0
     z1 = karastuba(x1, y1, k)         # 计算x1y1
     z2 = karastuba((x1 + x0), (y0 + y1), k) - z1 - z0

     return z1 * (10 ** n) + z2 * (10 ** k) + z0

　　然而运行时会发现这段代码很难生效，原因是计算时要求的环境太过理想——每次迭代时x_i和y_i的位数都必须相同。这就需要重新审视Karastuba算法，看看非理想状态下是如何计算的。

　　假设x和y分别是m位和n位的大整数，x和y可以这样分解：

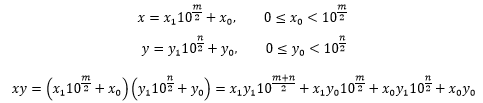
　　反复迭代x_iy_i，直到其中一个乘数只有1位为止。

　　示例： 123×321 = ?

　　

　　现在可以编写能够正确运行的大整数乘法代码：

 def karastuba(x, y):
     ''' karastuba算法计算两个n位的大整数乘法, x >=0, y >= 0 '''
     if x == 0 or y == 0:
         return 0
     m, n = len(str(x)), len(str(y)) # x和y的位数
     if m == 1 or n == 1: # 如果x或y只有1位，直接计算结果
         return x * y
     m //= 2
     x1, x0 = x // (10 ** m), x % (10 ** m) # 分解x
     n //= 2
     y1, y0 = y // (10 ** n), y % (10 ** n) # 分解y
     # 迭代分解够的4个较小规模的乘法
     x1y1 = karastuba(x1, y1)
     x1y0 = karastuba(x1, y0)
     x0y1 = karastuba(x0, y1)
     x0y0 = karastuba(x0, y0)
     return x1y1 * (10 ** (m + n)) + x1y0 * (10 ** m) + x0y1 * (10 ** n) + x0y0

 def paint(x, y):
     ''' 在控制台打印karastuba(x, y)的运行结果 '''
     print('{0} * {1} = {2}, ({3})'.format(x, y, karastuba(x, y), x * y))

 if __name__ == '__main__':
     paint(123, 321)
     paint(123456789, 987456)
     paint(1234567891234567, 1234567891234567)

　　先看看windows计算器下1234567891234567×1234567891234567的运行结果：

　　计算器已经无法给出精确的结果，但karastuba没有问题：

　　对于非10进制整数，Karastuba算法依然适用。

　　

---

　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！

　　扫描二维码关注公众号“我是8位的”