重新整理数据结构与算法（c#系列）—— 树的前中后序遍历查找[十七]

前言

树的前中后序遍历 是根据前中后序的顺序来查找，找到了则弹出。

正文

节点模型:

public class HeroNode
{
	private int no;

	private string name;

	private HeroNode left;

	private HeroNode right;

	public HeroNode(int no, string name) {
		this.no = no;
		this.name = name;
	}

	public int getNo() {
		return no;
	}
	public void setNo(int no)
	{
		this.no = no;
	}

	public String getName()
	{
		return name;
	}
	public void setName(String name)
	{
		this.name = name;
	}
	public HeroNode getLeft()
	{
		return left;
	}
	public void setLeft(HeroNode left)
	{
		this.left = left;
	}
	public HeroNode getRight()
	{
		return right;
	}
	public void setRight(HeroNode right)
	{
		this.right = right;
	}
	public override string ToString()
	{
		return "姓名:" + name + "编号:" + no;
	}
	//编写前序遍历的方法 是根、左、右
	public void preOrder() {
		Console.WriteLine(this);

		if (this.left != null)
		{
			this.left.preOrder();
		}
		if (this.right != null)
		{
			this.right.preOrder();
		}
	}
	//中序遍历 是左、根、右
	public void infixOrder() {
		if (this.left != null)
		{
			this.left.infixOrder();
		}
		Console.WriteLine(this);
		if (this.right != null)
		{
			this.right.infixOrder();
		}
	}
	// 后续遍历为 左、右、根
	public void postOrder()
	{
		if (this.left != null)
		{
			this.left.postOrder();
		}
		if (this.right != null)
		{
			this.right.postOrder();
		}
		Console.WriteLine(this);
	}
	//前序遍历查找
	public HeroNode preOrderSearch(int no)
	{
		HeroNode resNode = null;
		record();
		if (this.no == no)
		{
			return this;
		}
		if (this.left != null)
		{
			resNode=this.left.preOrderSearch(no);
		}
		if (resNode != null)
		{
			return resNode;
		}
		if (this.right != null)
		{
			resNode = this.right.preOrderSearch(no);
		}
		return resNode;
	}

	//中序遍历查找

	public HeroNode infixOrderSearch(int no)
	{
		HeroNode resNode = null;
		if (this.left != null)
		{
			resNode = this.left.infixOrderSearch(no);
		}
		if (resNode != null)
		{
			return resNode;
		}
		record();
		if (this.no == no)
		{
			return this;
		}
		if (this.right != null)
		{
			resNode = this.right.infixOrderSearch(no);
		}
		return resNode;
	}

	//后序遍历查找

	public HeroNode postOrderSearch(int no)
	{

		  HeroNode resNode = null;

		if (this.left != null)
		{
			resNode = this.left.postOrderSearch(no);
		}
		if (resNode != null)
		{
			return resNode;
		}

		if (this.right != null)
		{
			resNode = this.right.postOrderSearch(no);
		}
		if (resNode != null)
		{
			return resNode;
		}
		record();
		if (this.no == no)
		{
			resNode=this;
		}
		return resNode;
	}
	public void record()
	{
		Console.WriteLine("查找步骤为:名字" + this.name + " 编号:" + this.no);
	}
}

树模型:

public class BinaryTree
{
	private HeroNode root;

	public void setRoot(HeroNode root)
	{
		this.root = root;
	}
	//前序遍历
	public void preOrder()
	{
		if (this.root != null)
		{
			this.root.preOrder();
		}
		else
		{
			Console.WriteLine("二叉树为空，无法遍历");
		}
	}

	//中序遍历
	public void infixOrder()
	{
		if (this.root != null)
		{
			this.root.infixOrder();
		}
		else
		{
			Console.WriteLine("二叉树为空，无法遍历");
		}
	}
	//后序遍历
	public void postOrder()
	{
		if (this.root != null)
		{
			this.root.postOrder();
		}
		else
		{
			Console.WriteLine("二叉树为空，无法遍历");
		}
	}
	//前序遍历查找
	public HeroNode preOrderSearch(int no)
	{
		if (root != null)
		{
			return this.root.preOrderSearch(no);
		} else {
			return null;
		}
	}
	//中序遍历查找
	public HeroNode infixOrderSearch(int no)
	{
		if (root != null)
		{
			return this.root.infixOrderSearch(no);
		}else
		{
			return null;
		}
	}
	//后序遍历查找
	public HeroNode postOrderSearch(int no)
	{
		if (root != null)
		{
			return this.root.postOrderSearch(no);
		}else {
			return null;
		}
	}
}

测试:

static void Main(string[] args)
{
	//先需要创建一颗二叉树
	BinaryTree binaryTree = new BinaryTree();
	//创建需要的结点
	HeroNode root = new HeroNode(1, "宋江");
	HeroNode node2 = new HeroNode(2, "吴用");
	HeroNode node3 = new HeroNode(3, "卢俊义");
	HeroNode node4 = new HeroNode(4, "林冲");
	HeroNode node5 = new HeroNode(5, "关胜");
	//设置节点
	root.setLeft(node2);
	root.setRight(node3);
	node3.setRight(node4);
	node3.setLeft(node5);
	binaryTree.setRoot(root);
	//前序遍历
	Console.WriteLine("前序遍历查找");
	binaryTree.preOrderSearch(5);
	Console.WriteLine("中序遍历查找");
	binaryTree.infixOrderSearch(5);
	Console.WriteLine("后续遍历查找");
	binaryTree.postOrderSearch(5);
	Console.ReadKey();
}

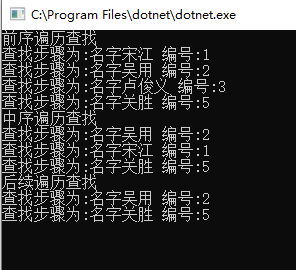
测试结果: