2021-04-09：rand指针是单链表节点结构中新增的指针，rand可能指向链表中的任意一个节点，也可能指向null。给定一个由Node节点类型组成的无环单链表的头节点 head，请实现一个函数完成这个链表的复制，并返回复制的新链表的头节点。 【要求】时间复杂度O(N)，额外空间复杂度O(1) 。

2021-04-09：rand指针是单链表节点结构中新增的指针，rand可能指向链表中的任意一个节点，也可能指向null。给定一个由Node节点类型组成的无环单链表的头节点 head，请实现一个函数完成这个链表的复制，并返回复制的新链表的头节点。 【要求】时间复杂度O(N)，额外空间复杂度O(1) 。

福大大 答案2021-04-09：

假设链表节点是A1→B1→C1。

1.复制节点，插入原链表，链表变成A1→A2→B1→B2→C1→C2。

2.设置A2、B2、C2的随机指针。

3.拆分链表。变成A1→B1→C1和A2→B2→C2。

4.返回A2→B2→C2。

代码用golang编写。代码如下：

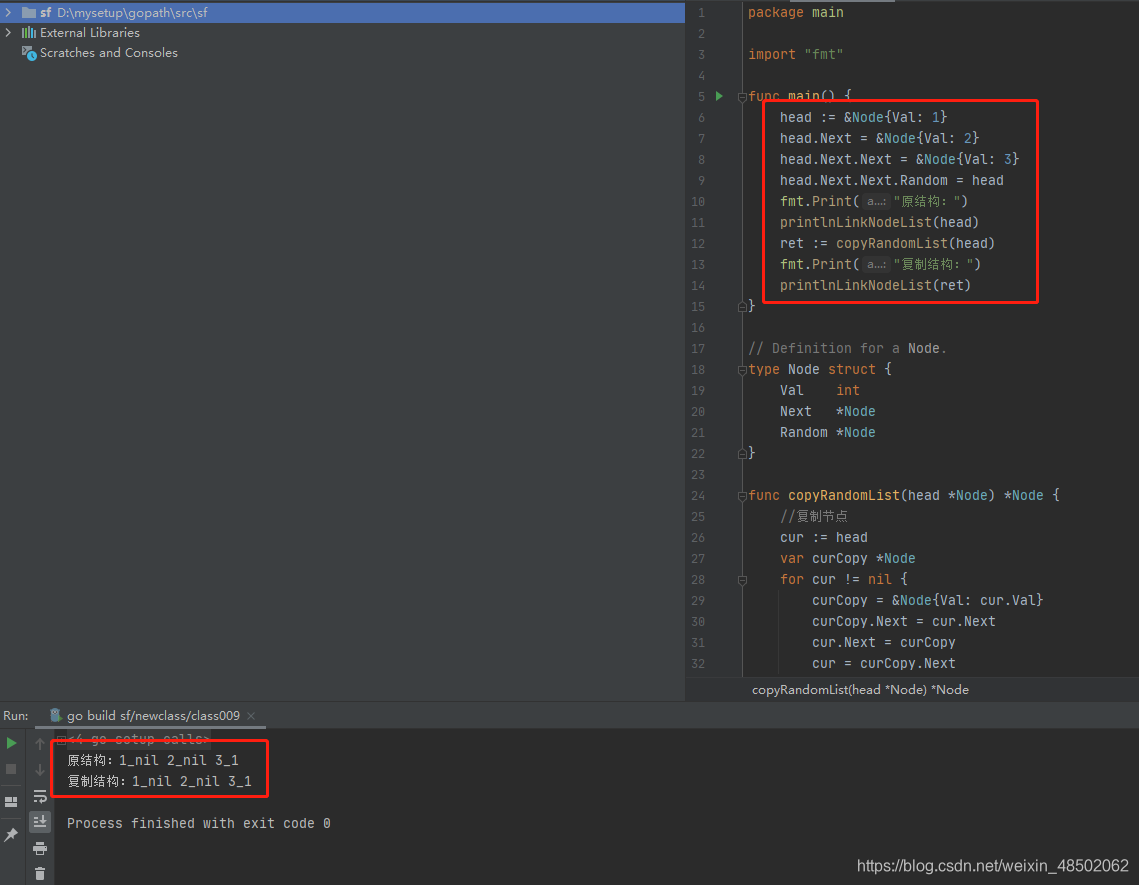
package main

import "fmt"

func main() {
    head := &Node{Val: 1}
    head.Next = &Node{Val: 2}
    head.Next.Next = &Node{Val: 3}
    head.Next.Next.Random = head
    fmt.Print("原结构：")
    printlnLinkNodeList(head)
    ret := copyRandomList(head)
    fmt.Print("复制结构：")
    printlnLinkNodeList(ret)
}

// Definition for a Node.
type Node struct {
    Val    int
    Next   *Node
    Random *Node
}

func copyRandomList(head *Node) *Node {
    //复制节点
    cur := head
    var curCopy *Node
    for cur != nil {
        curCopy = &Node{Val: cur.Val}
        curCopy.Next = cur.Next
        cur.Next = curCopy
        cur = curCopy.Next
    }
    //设置随机节点
    cur = head
    for cur != nil && cur.Next != nil {
        if cur.Random != nil {
            cur.Next.Random = cur.Random.Next
        }
        cur = cur.Next.Next
    }

    //分离成两个链表
    cur = head
    headCopy := head.Next
    for cur != nil && cur.Next != nil {
        next := cur.Next
        cur.Next = cur.Next.Next
        cur = next
    }

    //返回复制链表
    return headCopy
}

//链表打印
func printlnLinkNodeList(head *Node) {
    cur := head
    for cur != nil {
        if cur.Random != nil {
            fmt.Print(cur.Val, "_", cur.Random.Val, " ")
        } else {
            fmt.Print(cur.Val, "_nil ")
        }
        cur = cur.Next
    }
    fmt.Println()
}

执行结果如下：

---

左神java代码

力扣138. 复制带随机指针的链表

评论