NLP复习之神经网络

NLP复习之神经网络

前言

tips：

• 设计神经网络时，输入层与输出层节点数往往固定，中间层可以自由指定；
• 神经网络中的拓扑与箭头代表预测过程数据流向，与训练的数据流有一定区别；
• 我们不妨重点关注连接线，因为它们是权重，是要训练得到的

神经元

神经元模型是一个包含输入、输出、计算功能的模型，注意中间的箭头线，称之为“连接”，上面有“权值”

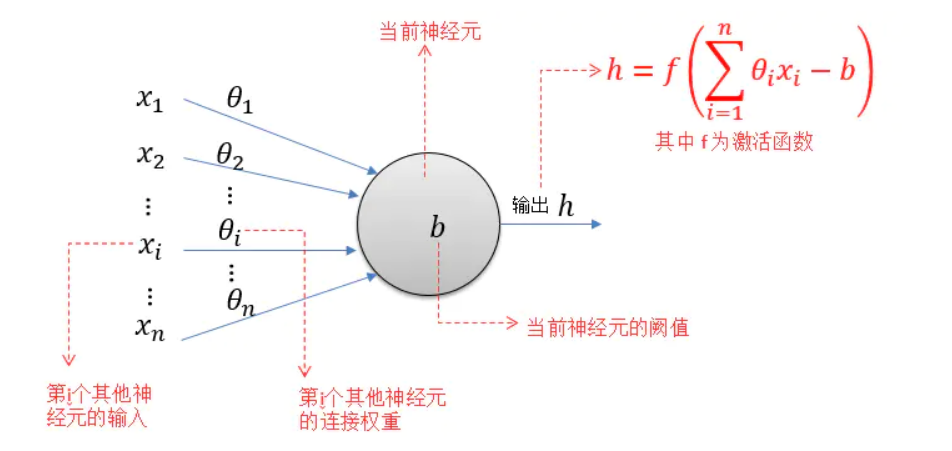
​ 一个神经网络的训练算法就是让权重的值调整到最佳，以使得整个网络的预测效果最好。

MP神经元模型接收来自n个其他神经元传递过来的输入信号（x1~xn），这些输入信号通过带权重（θ或ω来表示权重，上图采用θ）的连接（Connection）进行传递，然后神经元（图示阈值为b）收到的总输入（所有输入和权重的乘积的和）与神经元的阈值b比较，并经由激活函数（Activation Function，又称响应函数）处理之后产生神经元的输出。

理想情况下，激活函数的形式应为阶跃函数（也就是修正线性单元ReLU），通常选择Sigmoid函数：

\[Sigmoid(x)=S(x)=\frac{1}{1+e^{-x}}
\]

其值域为\((0,1)\)。

​ 神经元可以看做一个计算与存储单元，计算是神经元对其的输入进行计算，存储是神经元会暂存计算结果，传递到下一层。

多层神经网络

单层神经网络（感知机）在此处暂时忽略不写，期末要挂科了

上图展现了基本两层神经网络，其中\(x_i(i=1, 2, 3)\)为输入层值，\(a_i^{(k)}(k=1, 2, \dots, K; i = 1, 2, 3, \dots, N_k)\)表示第k层中，第i个神经元的激活值，\(N_k\)表示第k层的神经元个数。当k=1时，即为输入层，即\(a_i^{(1)}=x_i\)，而\(x_0=1\)和\(a_0^{(2)}=1\)为偏置项

为了求最后的输出值\(h_{\theta}(x)=a_1^{(3)}\)，我们需要计算隐藏层中每个神经元的激活值\(a_{ji}^{(k)}(k=2,3)\)，而隐藏层/输出层的每一个神经元，都是由上一层神经元经过类似逻辑回归计算得到。

反向传播（BP算法）

给出一个示例，是我们的作业题目

（1）在该例子中什么是输入层，隐藏层，输出层，并对不同的层和层之间的权重矩阵进行维度标记。

（2）使用链式法则，在损失函数L上，分别对\(z^{[2]}，z^{[1]}_1，z^{[1]}_2，x_1，x_2\)，进行求偏导

解

（1）

输入层：\(x_1,x_2\)，维度为\(2 \times 1\);

输入层与隐藏层之间的权重矩阵：\(w_{11}^{[1]},w_{12}^{[1]}，w_{21}^{[1]},w_{22}^{[1]}\)，维度为\(2 \times 2\);

经过加权求和与偏置后，得到：\(z_1^{[1]},z_2^{[1]}\)，维度为\(2 \times 1\);

经过ReLU激活函数后得到隐藏层：\(a_1^{[1]},a_2^{[1]}\)，维度为\(2 \times 1\);

隐藏层与输出层之间的权重矩阵：\(w_{11}^{[2]},w_{12}^{[2]}\)，维度为\(1 \times 2\);

经过加权求和与偏置后，得到：\(z^{[2]}\)，维度为\(1 \times 1\);

经过sigmoid激活函数后得到输出层：\(a^{[2]}\)，维度为\(1 \times 1\)。

（2）

损失函数：

\[L = -[y \log{a^{[2]}} + (1 - y) \log{(1 - a^{[2]})}]
\]

所有表达式：

\[\begin{aligned}
a^{[2]} &= \sigma{(z^{[2]})} \\
z^{[2]} &= w_{11}^{[2]}a_1^{[1]} + w_{12}^{[2]}a_2^{[1]} + b_1^{[2]} \\
a_1^{[1]} &= ReLU(z_1^{[1]}) \\
a_2^{[1]} &= ReLU(z_2^{[1]}) \\
z_1^{[1]} &= w_{11}^{[1]}x_1 + w_{12}^{[1]}x_2 + b_1^{[1]} \\
z_2^{[1]} &= w_{21}^{[1]}x_1 + w_{22}^{[1]}x_2 + b_2^{[1]}
\end{aligned}
\]

阶段求导：

\[\begin{aligned}
\frac{\partial L}{\partial a^{[2]}} &= - [\frac{y}{a^{[2]}} + \frac{y - 1}{1 - a^{[2]}}] \\
\frac{\partial a^{[2]}}{\partial z^{[2]}} &= \sigma{(z^{[2]})}(1-\sigma{(a^{[2]})}) = a^{[2]}(1 - a^{[2]}) \\
\frac{\partial z^{[2]}}{\partial a_1^{[1]}} &= w_{11}^{[2]} \\
\frac{\partial z^{[2]}}{\partial a_2^{[1]}} &= w_{12}^{[2]} \\

\frac{\partial a_1^{[1]}}{\partial z_1^{[1]}} &= \begin{cases} 0,\text{for } z_1^{[1]} < 0 \\ 1,\text{for } z_1^{[1]} \geq 0 \end{cases} \\
\frac{\partial a_1^{[1]}}{\partial z_2^{[1]}} &= \begin{cases} 0,\text{for }
z_2^{[1]} < 0 \\ 1, \text{for } z_2^{[1]} \geq 0 \end{cases} \\
\frac{\partial z_1^{[1]}}{\partial x_1} &= w_{11}^{[1]},\frac{\partial z_1^{[1]}}{\partial x_2} = w_{12}^{[1]},\frac{\partial z_2^{[1]}}{\partial x_1} = w_{21}^{[1]},\frac{\partial z_2^{[1]}}{\partial x_2} = w_{22}^{[1]}
\end{aligned}
\]

链式求导：