P1737

problem

---

\(\text{task 1}\)

要求：

输入：\(a,b\)。

输出：\(-2a-2b\)。

数据范围：\(|a|,|b| \le 10^9\)。

做法：

先把 \(-2\) 提出来，所以得 \(-2a-2b=-2(a+b)\)。

然后我们可以把 \(2\) 变成 \(1\) 右移 \(1\) 位。

code:

---

\(\text{task 2}\)

要求:

输入: \(a\)。

输出：\(\dfrac{1}{1 + e^{17a}}\)。

数据范围：\(|a| \le 10^9\)。

做法：

\(\dfrac{1}{1+e^{17a}} = \dfrac{1}{1+e^{-(2^4 a+a)}}\)。

所以就知道怎么写啦！！

代码：

---

\(\text{test 3}\)

要求：

输入: \(a\)。

输出：\(\dfrac{|a|}{a}\)。

数据范围：\(|a| \le 10^9\)。

做法：

1. \(6pts\) 做法

先整出 \(-x\)，然后把 \(-x+x\) 就可以得到 \(0\) 了。然后再跟 \(x\) 比较即可获得 \(6\) 分。

1. 满分做法

考虑为什么题目会给出 精度 这一概念，为什么会给出 \(f(0) = 0.5\) 且 \(f(+ \infty) = 1\) 且 \(f(- \infty) = 0\)。

我们可以直接把这个数乘上 \(2^{1000}\) 这样子直接让它变成 \(0\)，所以我们就有 \(f(0)\) 了，然后我们在把这个数 \(-0.5\) 就可以得到 \(0\) 了。

---

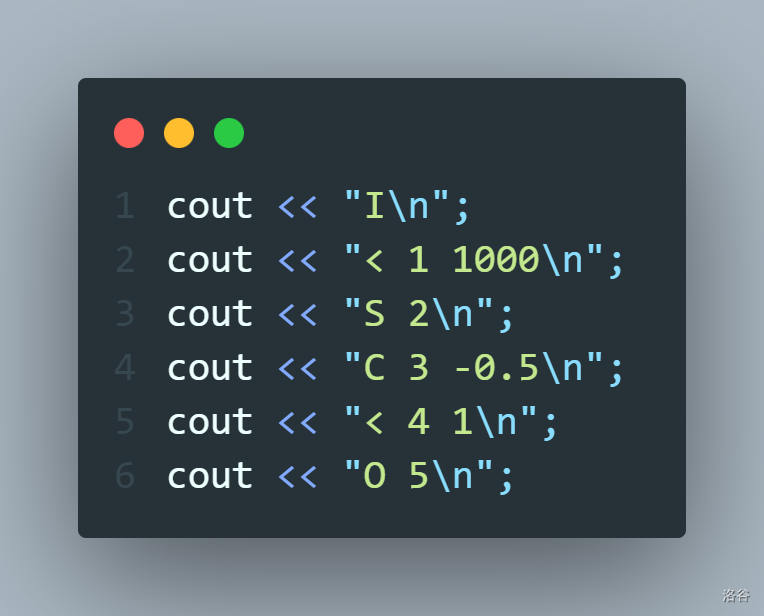
\(\text{test 4}\)

要求：

输入：\(a\)。

输出：\(|a|\)

做法：

我们发现 \(\dfrac{S(x) - S(0)}{x} = \frac{1}{4}\)，所以 \(S(x)\) 就约等于 \(\dfrac{x}{4}+0.5\)。

如果是正数，我们可以利用上一题的思路。

我们令 \(t = S(x << \infty) << \infty\)，然后带入 \(S(x >> \infty + t)\)，易知当 \(x > 0\) 时，答案是 \(1\)。

重复上面的操作我们就可以得到 \(0.5 << \infty\)，然后加上 \(t\) 即可。

代码：

---

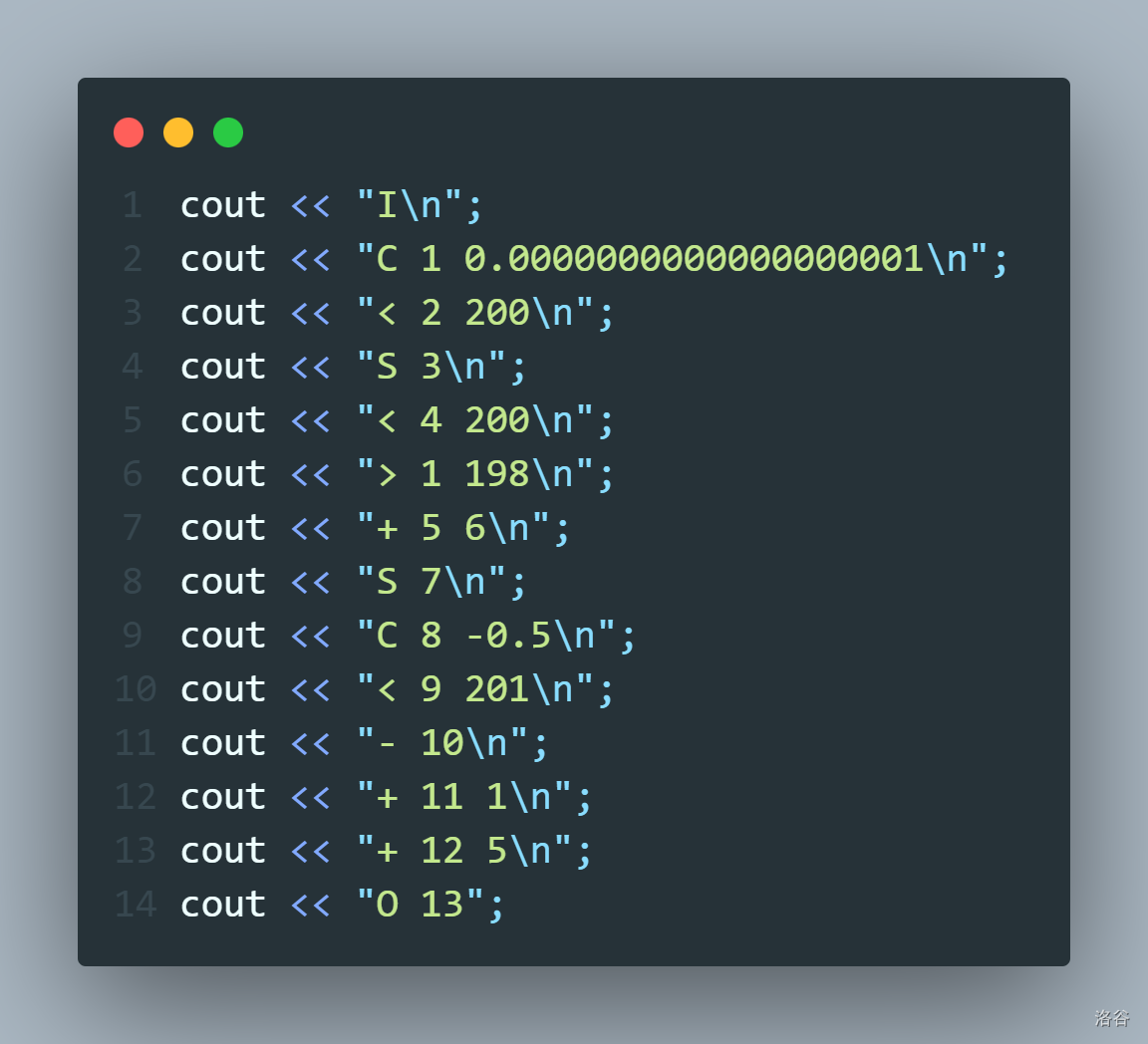
\(\text{test 5}\)

要求：

输入：\(a_1,a_2 \cdots \cdots a_{32}\)。

输出： 把 \(a_1,a_2 \cdots \cdots a_{32}\) 从左到右看成一个二进制整数，高位在左低位在右，输出该整数的值。

做法：

经过了两道难题之后，终于有迎接了一道简单题了。

直接按照题意模拟即可。

这个就不扔了。

---

\(\text{test 6}\)

要求：

输入：一个数 \(a\)。

输出：把他拆成 \(32\) 位。

做法：

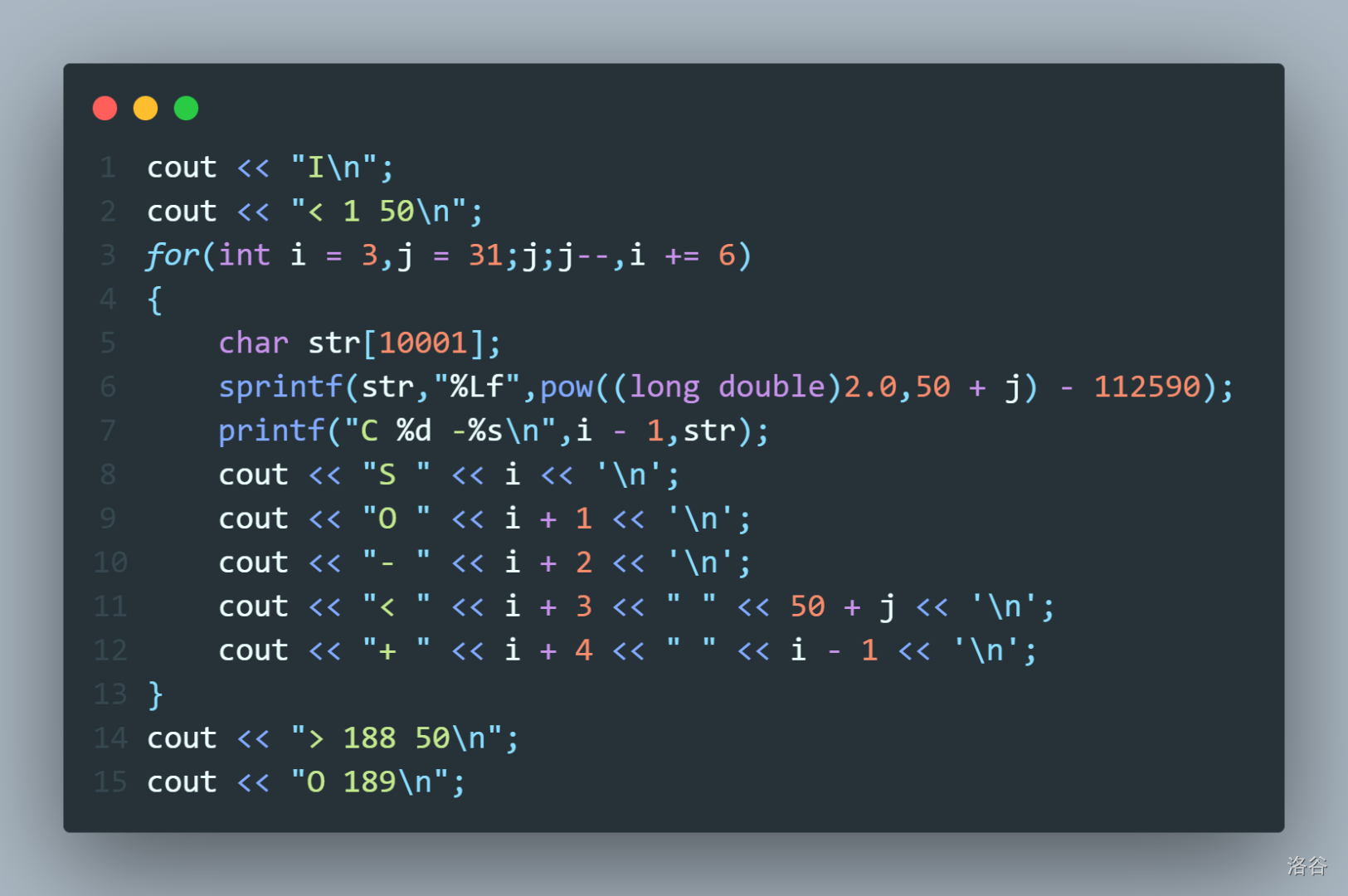
我们令 \(a_1 = a - 2^t [a \ge 2^t]\)，然后 \(a_1\) 又是一个最多只有 \(t-1\) 位的数字，然后重复上面的操作即可。

然后问题就回到了 \(\text{test 3}\) 的比大小了。

然后就是和 \(\text{test 4}\) 同样的问题。每一次都会偏移，所以我们作整个数统一偏移 \(10^{-10}\)。