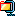An expression evaluator

An expression evaluator

 Download source code (17 kb)

Two weeks ago, I saw an article on codeproject that really nicely solve an old and very known issue. Why it is nice is because it is short, simple, sequential
and last but not least elegant.

In the mean time, I needed an expression evaluator for a product I am making, and I needed not only to extend the principles of evaluation, but also add a few features.

This article describes what I have done in order to write a general purpose expression evaluator, that goes beyond evaluating the 4 primary operations. In fact it can be regarded as a complement to the mentioned article for three reasons :

• it's a complete rewrite
• it uses an object model when it comes to variables and functions
• it describes how the parsing and evaluation works

The principles of expression parsing

It's an old problem because although separating operators from numbers or other tokens is an easy task, the fact that operators are either infix or not, and have algebric prevalence relations between them forces the parser to pay a particular attention to
the whole parsing process. Quite naturally, this involves playing with a separate stack of all operators, and swapping operators according to a set of predefined rules.

The good news is that, when it comes to usual mathematical expressions, there are only a tiny set of rules. Here they are :

• * and / are prevalent over + and -
• functions are prevalent over * and /
• parenthesis are always prevalent over operators

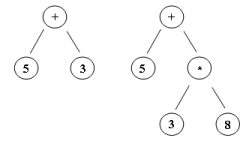
What prevalent means is that if operator a is prevalent over operator b, then a will be performed before b. For instance, multiplications must be performed before additions. Of course, parenthesis help solve prevalence
issues.

Other than prevalence, we need to build a tree of operations to perform in order to get a result out of the evaluation. Typical trees are binary trees where operands are leaves, and operators are tree nodes. Of course, because operators can chain up each
other arbitrarily, the tree can be fairly deep, and significantly unbalanced (by the way, re-balancing trees is an interesting topic). Below are example pics of evaluation trees for the following expressions : = 5 + 3, =
5 + 3 * 8.

Sample evaluation trees

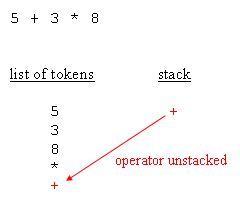
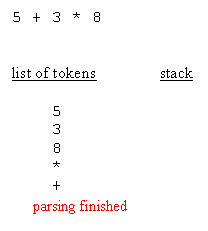
When an evaluation tree is built, evaluation can be done by traversing the nodes from the root down to leaves. Doing the evaluation is a matter of knowing, for each operator, how many arguments are expected, and retrieve them recursively going down the tree.

That being said, and that's the main point of RPN (Reverse Polish Notation), an actual tree need not be created. Having an expression in which operators are suffixes of their arguments is enough to have the equivalent of the tree and, as a result, enough
to do the evaluation.

For instance, the parsing phase not only distinguishes operator arguments, better known as operands, and operators themselves, the parsing phase also repurposes the expression so that it's in RPN style. For the sample expressions, =
5 + 3, and = 5 + 3 * 8, this leads to : {5}{3}{+} and {5}{3}{8}{*}{+}.

RPN makes evaluation straight forward

Why RPN is so useful is that, given such order, it is possible to have a really simple algorithm that reads tokens from left to right, stacks all operands, and then unstacks those whenever an operator is retrieved. After the operation is performed, the resulting
token is stacked so it behaves to the remainder of the RPN expression like a normal operand. Below provides a timeline evaluation process of expression = 5 + 3 * 8 :

• Tokens are from this list : {5}{3}{8}{*}{+}
• next token is {5}, an operand, stack it (separate stack), stack now contains {5}
• next token is {3}, an operand, stack it, stack now contains {5} {3}
• next token is {8}, an operand, stack it, stack now contains {5} {3} {8}
• next token is {*}, operator, 2 expected operands, unstack two operands ({3} {8}), perform the operation, stack the result, stack now contains {5} {24}
• next token is {+}, operator, 2 expected operands, unstack two operands ({5} {24}), perform the operation, stack the result, stack now contains {29}
• the token list is empty
• {29} is the result of evaluation!

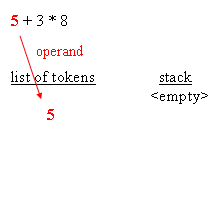
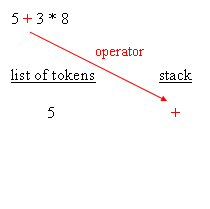
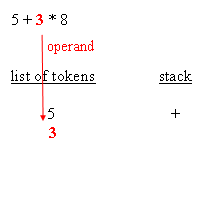
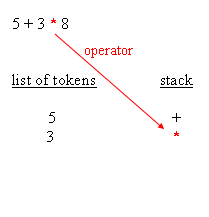
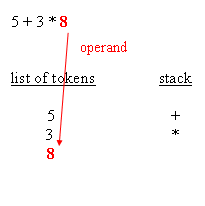
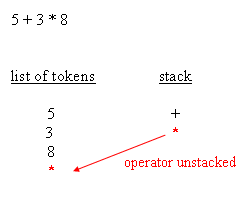
Please note that, during the evaluation process, it is possible to check the expected number of arguments against the amount of arguments available in the operand stack. This leads to typical execution errors, where the user is expected to correct the impaired
arguments being passed. In order to forge a cursor position for that execution error, the tokens must be associated to a cursor position from the original expression.

A typical algorithm for expression parsing is as follows :

 for each char of the expression
   decide if the char is part of an operand or of an operator
   if the char is part of an operand,
     append it to the list of operands
   else if the char is part of an operator,
     look up the operator
	 match it with supported operators
	 compare operator with the preceding operators
	 if this operator is prevalent,
	   store the operator in a stack
     otherwise, unstack the preceding operator,
                append the preceding operator to the list of operands
                stack the new operator
	 end if
   end if
 end for

This is a general algorithm and it's easy to figure out that a typical implementation remains under 200 lines of source code.

The following blocks depict how the parsing works :

initial structures

retrieving an operand

retrieving an operator

retrieving an operand

retrieving an operator

retrieving an operand

unstacking the operator from the top of the stack

unstacking the operator from the top of the stack

RPN style of the resulting structure

If the expression was = 5 * 3 + 8, instead of = 5 + 3 * 8, then when the parser retrieves the + operator, it unstacks the * operator and append it to the list of tokens, before the + operator is stacked.

Since parenthesis are of maximum prevalence, they have to be taken into account as such. While open and closed parenthesis behave like any other normal operators, they are paid a special attention. Parenthesis are not appended in the list of tokens. What
parenthesis do is only add an arbitrary prevalence on top of the existing prevalence order between stacked operators. When parsing the expression, any time we reach a closed parenthesis, we basically unstack all operators until we reach the open parenthesis.
This is how maximum prevalence is sorted out.

In the implementation provided in this article, a more granular level of object manipulation was considered. If we limit ourselves to what has been said above, then this expression evaluator is limited to the simple operators. We neither support functions
nor variables. What would be an expression evaluator good for is it doesn't support both of these?

Implementing the list of tokens is a matter of having a base class, wzelement, whose derived classes either hold numbers, strings, operators, or whatever might be required by the client application. As a result, the list of tokens is an array of wzelement
:

typedef enum {_operator, _litteral} elementtype;

wzarray<wzelement*> m_arrelements; // list of tokens

Just to show how this is brought together, below is the declarations for those classes :

class wzelement
{
protected:
  elementtype m_type;

public:
  wzelement();
  virtual ~wzelement();

  void setType(elementtype t);
  elementtype getType();

};

class wzoperator : public wzelement
{
protected:
  long m_nID;
  long m_nPriority;
  long m_nbParams;
  BOOL m_bIsAfunction;

public:
  void setID(long n);
  long getID();

  void setPriority(long lvl);
  long getPriority();

  void setNbParams(long nb);
  long getNbParams();

  void setIsAFunction(BOOL bIsAFunction);
  BOOL getIsAFunction();

  BOOL isHigherPriorityThan(wzoperator* src); // TRUE if this is of higher priority than src
  BOOL isParenthesis();
};

// wzstring //////////////////////////////////////////////
//
// simple string storage implementation
//
class wzstring : public wzelement
{

  // Members
protected:
  LPSTR	m_pstr;
  long	m_nLength;

  // Construction
public:
  wzstring();
  virtual ~wzstring(); // frees the buffer

  void init();

  BOOL isEmpty();

  void empty();
  LPSTR setString(LPSTR pString, long nLength); // allocates a buffer
  LPSTR setString(wzstring* pString); // allocates a buffer
  LPSTR getString();
  long getLength();

  BOOL isANumber(); // TRUE if the number is an integer
  BOOL isADouble(); // less restricting than isANumber()
  long getNumber();
  double getDouble();

  void fromNumber(long n);
  void fromDouble(double d);

//void fromNumberOrDouble(double d, BOOL bArg1IsANumber, BOOL bArg2IsANumber);
  void fromNumberOrDouble(double d, ...); // var args implementation

};

Function support

Supporting functions is a matter of :

• adding operator tokens to the list of supported operators
• adding a special treatment whenever the parser finds an argument separator.

Adding support to functions gives a good opportunity to declare operators openly in a table, rather than hardcode them in the parser. Among important flags required by either the parser or the evaluator are :

• the amount of arguments expected by the operator. This can be 0, 1, 2, ...
• whether the operator is a function or not. This plays a role to better identify parenthesis used to manage prevalence or parenthesis enclosing function arguments.
• the prevalence of that operator
• last but not least, its ID

Below is a sample table showing exactly that :

_structoperator operators[] = {
  { "+"/*label*/, 50/*id*/, 10/*priority*/, 2/*nbparams*/, FALSE/*is a function*/ },
  { "-",          51,       10,             2,             FALSE },
  { "*",          52,       20,             2,             FALSE },
  { "/",          53,       20,             2,             FALSE },
  { "(",          40,       100,            1,             FALSE },
  { ")",          41,       100,            1,             FALSE },
  { "SIN",        60,       30,             1,             TRUE },
  { "COS",        61,       30,             1,             TRUE },
  { NULL,          0,        0,             0,                0 }
};

Although the table above (and by the way the source code provided) implements functions that play with numbers, it need not be the case. As a matter of fact, arguments can be strings, imbricated functions or operators, etc. For instance, this source code
is used to create Excel formulas like this : =IF(B2 > B3 ; IF(B3 > B4 ; "TRUE" ; "FALSE" ) ; "FALSE").

Last but not least, the argument separator, ; by default, can be specified using the parser API. Unlike typical comma-separated C-code arguments, functions tend to use semi-colons any time arguments can be numbers. Indeed,
commas can be thousand or decimal separators depending on the culture. It is possible to allow comma-separated functions as long as tokens are enclosed within quotes, but this is an unnecessary overhead, causes user look and feel issues, and makes the expression
looks odd.

Variables support

Supporting variables is only a matter of replacing litteral tokens that are not numbers, strings or other litterals with actual numbers or strings or whatever is suited to performing operations.

In order to call the evaluator more than once, either the list of tokens must be saved somewhere, and then restored, or variables being replaced with their value need to put back their original name, in the evaluation clean up. In the provided source code,
we clean up the evaluation process by putting original variable names back in the list of tokens.

The variable class is declared as follows :

class wzvariable : public wzelement
{

  // Members
protected:
  wzstring m_varname, m_varvalue;
  wzstring* m_attachedLitteral;

public:
  void setVar(LPSTR name, LPSTR value);
  void setVarname(LPSTR name);
  void setVarvalue(LPSTR value);

  wzstring* getVarname();
  wzstring* getVarvalue();

  BOOL isNameMatching(wzstring* litteral);

  void attachLitteral(wzstring* litteral);
  wzstring* getLitteral();
};

Code samples

1) sample code

This sample code demoes the minimum code involved when parsing an expression. Variables not used.

#include "util.h"
#include "parser.h"

wzparser* p = new wzparser();

p->parse("=5+3+SIN(1.236)");
p->dump(); // for debug purpose only

wzarray<wzvariable*> arrVariables;

wzstring result;
if ( p->eval(arrVariables, result) )
{
  OutputDebugString( "result=" );
  OutputDebugString( result.getString() );
  OutputDebugString( "\r\n" );
}

delete p;

2) another sample code

This sample code uses variables. Evaluation is done twice as to show how to iterate the process.

#include "util.h"
#include "parser.h"

wzparser* p = new wzparser();

p->parse("=5+3+SIN(x)");
p->dump(); // for debug purpose only

wzarray<wzvariable*> arrVariables;

wzvariable* x = new wzvariable();
x->setVar("x","13");
arrVariables.Add( x );

wzstring result;
if ( p->eval(arrVariables, result) )
{
  OutputDebugString( "result=" );
  OutputDebugString( result.getString() );
  OutputDebugString( "\r\n" );
}

x->setVarvalue("15");
if ( p->eval(arrVariables, result) )
{
  OutputDebugString( "result=" );
  OutputDebugString( result.getString() );
  OutputDebugString( "\r\n" );
}

// delete variables
long nbVariables = arrVariables.GetSize();
for (long iVars = 0; iVars < nbVariables; iVars++)
  delete arrVariables.GetAt(iVars);

delete p;

3) what you need to reuse this code

You need the following files :

• util.h, util.cpp : element classes
• parser.h, parser.cpp : parser and evaluator
• it's pure C++ code. No dependency on MFC.

in parser.cpp, the operators table defines the support operators. When either the parser or evaluator fail, the getLastError() method returns the error.

History

• November 18, 2003 : first release. Support for basic functions.
• October 17, 2005 : second release. Much better parsing and eval routines. Support for variable length functions.

Stéphane Rodriguez

October 17, 2005.