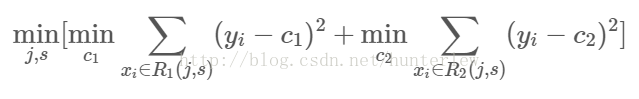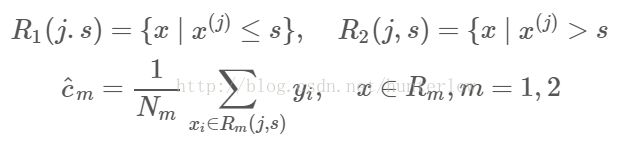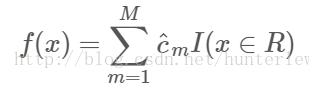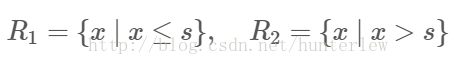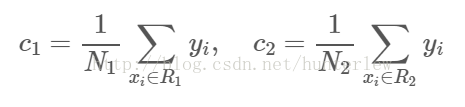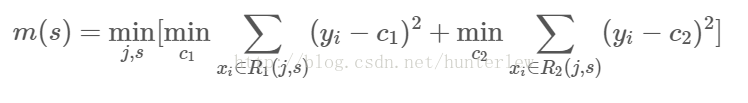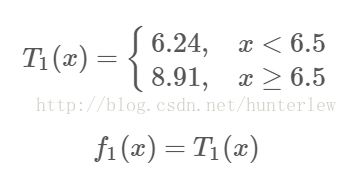CART回归树基本原理(具体例子)
id3不能直接处理连续性的特征,需要将连续性的转化成离散的,但是会破坏连续性特征的内在结构。
一、概念
CART全称叫Classification and Regression Tree。首先要强调的是CART假设决策树是二叉树,内部结点特征的取值只有“是”和“否”,左分支是取值为“是”的分支,有分支则相反。这样的决策树等价于递归地二分每个特征。
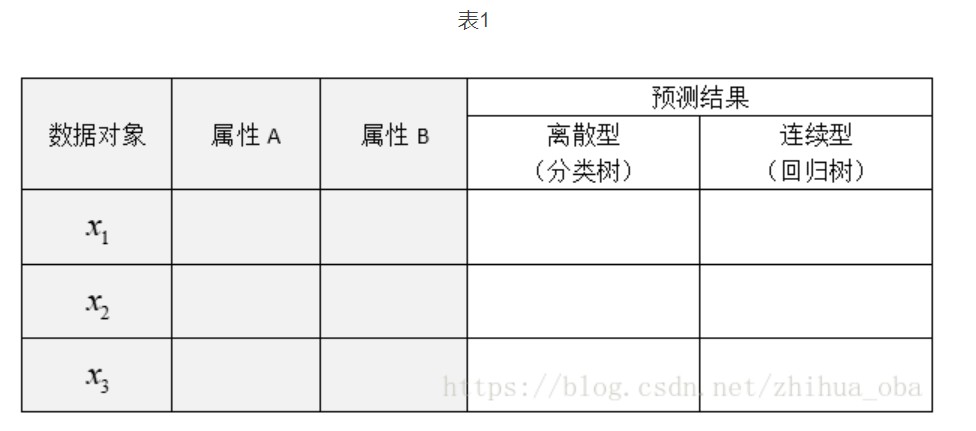
CART分类回归树是一种典型的二叉决策树,可以做分类或者回归。如果待预测结果是离散型数据,则CART生成分类决策树;如果待预测结果是连续型数据,则CART生成回归决策树。数据对象的属性特征为离散型或连续型,并不是区别分类树与回归树的标准,例如表1中,数据对象的属性A、B为离散型或连续型,并是不区别分类树与回归树的标准。作为分类决策树时,待预测样本落至某一叶子节点,则输出该叶子节点中所有样本所属类别最多的那一类(即叶子节点中的样本可能不是属于同一个类别,则多数为主);作为回归决策树时,待预测样本落至某一叶子节点,则输出该叶子节点中所有样本的均值。
二、CART生成
决策树的生成就是递归地构建二叉决策树的过程,对回归树用平方误差最小化准则,对分类树用基尼指数最小化准则,进行特征选择,生成二叉树。
三、回归树的生成最小二叉回归树生成算法:
1、选择最优切分变量j与切分点s,求解:
遍历变量j,对固定的切分变量j扫描切分点s,选择使上式取得最小值的对(j,s)。其中Rm是被划分的输入空间,Cm空间Rm对应的输出值。
2、用选定的对(j,s)划分区域并决定相应的输出值:
3、继续对两个子区域调用步骤1,直至满足停止条件。
4、将输入空间划分为M个区域R1,R2,...Rm生成决策树:
四、示例
上面的东西有点难以理解,下面举个例子来说明。
训练数据见下表,x的取值范围为区间[0.5,10.5],y的取值范围为区间[5.0,10.0],学习这个回归问题的最小二叉回归树。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 5.56 | 5.70 | 5.91 | 6.40 | 6.80 | 7.05 | 8.90 | 8.70 | 9.00 | 9.05 |
求解训练数据的切分点s:
容易求得在R1、R2内部使得平方损失误差达到最小值的c1、c2为:
这里N1、N2是R1、R2的样本点数。
求训练数据的切分点,根据所给数据,考虑如下切分点:
1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5。
对各切分点,不难求出相应的R1、R2、c1、c2及
例如,当s=1.5时,R1={1},R2={2,3,...,10},c1=5.56,c2=7.50,则
现将s及m(s)的计算结果列表如下:
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
|---|---|---|---|---|---|---|---|---|---|
| m(s) | 15.72 | 12.07 | 8.36 | 5.78 | 3.91 | 1.93 | 8.01 | 11.73 | 15.74 |
由上表可知,当x=6.5的时候达到最小值,此时R1={1,2,...,6},R2={7,8,9,10},c1=6.24,c2=8.9,所以回归树T1(x)为:
CART回归树基本原理(具体例子)的更多相关文章
- CART回归树
决策树算法原理(ID3,C4.5) 决策树算法原理(CART分类树) 决策树的剪枝 CART回归树模型表达式: 其中,数据空间被划分为R1~Rm单元,每个单元有一个固定的输出值Cm.这样可以计算模型输 ...
- 大白话5分钟带你走进人工智能-第二十六节决策树系列之Cart回归树及其参数(5)
第二十六节决策树系列之Cart回归树及其参数(5) 上一节我们讲了不同的决策树对应的计算纯度的计算方法, ...
- 机器学习实战---决策树CART回归树实现
机器学习实战---决策树CART简介及分类树实现 一:对比分类树 CART回归树和CART分类树的建立算法大部分是类似的,所以这里我们只讨论CART回归树和CART分类树的建立算法不同的地方.首先,我 ...
- 作业三:CART回归树
作业三:CART回归树 20大数据三班 博客链接 学号 201613336 问题一: 表1为拖欠贷款人员训练样本数据集,使用CART算法基于该表数据构造决策树模型,并使用表2中测试样本集确定剪枝后的最 ...
- 决策树CART回归树——算法实现
决策树模型 选择最好的特征和特征的值进行数据集划分 根据上面获得的结果创建决策树 根据测试数据进行剪枝(默认没有数据的树分支被剪掉) 对输入进行预测 模型树 import numpy as np de ...
- 分类回归树(CART)
概要 本部分介绍 CART,是一种非常重要的机器学习算法. 基本原理 CART 全称为 Classification And Regression Trees,即分类回归树.顾名思义,该算法既 ...
- 回归树(Regression Tree)
目录 回归树 理论解释 算法流程 ID3 和 C4.5 能不能用来回归? 回归树示例 References 说到决策树(Decision tree),我们很自然会想到用其做分类,每个叶子代表有限类别中 ...
- 决策树算法原理(CART分类树)
决策树算法原理(ID3,C4.5) CART回归树 决策树的剪枝 在决策树算法原理(ID3,C4.5)中,提到C4.5的不足,比如模型是用较为复杂的熵来度量,使用了相对较为复杂的多叉树,只能处理分类不 ...
- 《机器学习Python实现_10_10_集成学习_xgboost_原理介绍及回归树的简单实现》
一.简介 xgboost在集成学习中占有重要的一席之位,通常在各大竞赛中作为杀器使用,同时它在工业落地上也很方便,目前针对大数据领域也有各种分布式实现版本,比如xgboost4j-spark,xgbo ...
- 【机器学习笔记之三】CART 分类与回归树
本文结构: CART算法有两步 回归树的生成 分类树的生成 剪枝 CART - Classification and Regression Trees 分类与回归树,是二叉树,可以用于分类,也可以用于 ...
随机推荐
- 渗透测试-前端验签绕过之SHA256+RSA
本文是高级前端加解密与验签实战的第2篇文章,本系列文章实验靶场为Yakit里自带的Vulinbox靶场,本文讲述的是绕过SHA256+RSA签名来爆破登录. 绕过 根据提示可以看出这次签名用了SHA2 ...
- COSBrowser 移动端——随时随地查看管理数据
外出身边没有电脑,需要查看管理数据怎么办? 出现紧急情况,需要快速停止某个 bucket 对外访问,怎么办? 个人用户仅作为网盘使用,需要方便轻量的管理工具,怎么办? 不用着急,COSBrowser ...
- 在docker中使用主机串口通讯
在进行软件docker化的过程时,很大的一个阻碍就是软件与各种外围硬件设备的交互,网口通信的设备能够很容易地接入容器,但是串口设备则要复杂一些.本文讨论在windows和linux下docker容器使 ...
- FISCO BCOS 控制台 部署合约 调用 查看已部署合约的地址
deploy 部署合约.(默认提供HelloWorld合约和TableTest.sol进行示例使用) 参数: 合约路径:合约文件的路径,支持相对路径.绝对路径和默认路径三种方式.用户输入为文件名时,从 ...
- virtualbox设置了共享文件夹却无权限访问
在virtualbox中设置共享文件夹后,然后登陆ubuntu系统访问共享文件夹,发现没有权限.查看共享文件夹的属性可知,共享文件夹的所有者是root,所属的组是vboxsf.以用户登录的时候,自然是 ...
- 龙哥量化:注册simnow上期所的期货仿真模拟交易账户教程步骤
永远顺着趋势交易 在技术分析这种市场研究方法中,趋势的概念绝对是核心内容.分析师所使用的全部工具, 诸如支撑和阻挡水平.价格形态.移动平均线.趋势线等等,其唯一的目的就是辅助我们估量市场趋势, 从而顺 ...
- Qt数据库应用16-通用数据库采集
一.前言 数据库采集对应的就是上一篇文章的数据库同步,数据库同步到云端数据库以后,app.网页.小程序啥的要数据的话,可以通过执行http请求拿到数据,http接收应答这边程序一般最简单可以用php写 ...
- Qt开源作品25-电池电量控件
一.前言 现在这个时代,智能手机不要太流行,满大街都是,甚至连爷爷奶奶级别的人都会用智能手机,本次要写的控件就是智能手机中的电池电量表示控件,采用纯painter绘制,其实也可以采用贴图,我估计大部分 ...
- error C2664: “HANDLE FindFirstFileW(LPCWSTR,LPWIN32_FIND_DATAW)”: 无法将参数 1 从“const _Elem *”转换为“LPCWSTR”
Error 30 error C2664: 'HANDLE FindFirstFileW(LPCWSTR,LPWIN32_FIND_DATAW)' : 不能将参数 1 从"char [260 ...
- Eclipse中如何将web应用部署到tomcat
第1种方法: 将workspace下的复制到tomcat的webapp下(我看度还是算了,看着都觉得麻烦). 第2种方法:总体思路就是:(1)先为web应用创建Tomcat Server:(2)再将w ...