数据挖掘 | 数据隐私（2） | 差分隐私 | 数据重构化攻击（Reconstruction Attacks）

L2-Reconstruction Attacks

本节课的目的在于正式地讨论隐私，但是我们不讨论算法本身有多隐私，取而代之去讨论一个算法隐私性有多么的不可靠。并且聚焦于 Dinur 与 Nissim 在论文所提出的一些启发差分隐私的理论。

同时，我们会重点分析一种称为重构攻击（Reconstruction Attacks）的攻击形式。

裂解聚合（Cracking Aggregation）

聚合（Aggregation）是一种常用的隐私保护方式，例如说在人口中将相同特征的个体聚合在一起

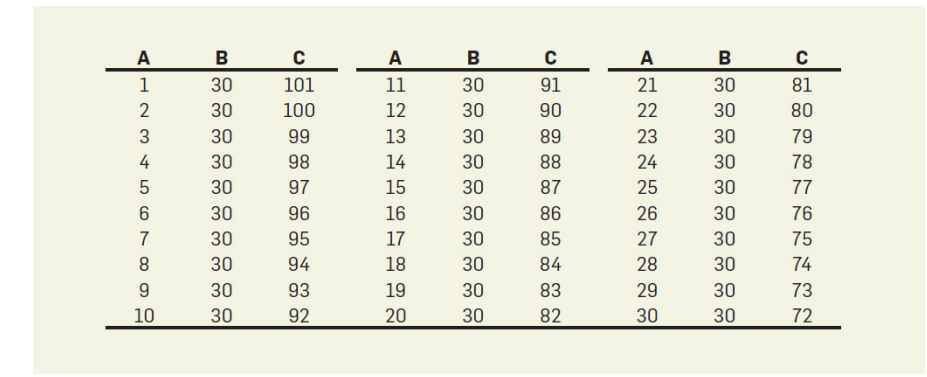
这是一个典型的例子

其标为\(D\)的因为数量太少而被抛弃

• 首先注意到表中有4位黑人，三位女黑人，为此可以推断出有一位男黑人
• 然后再通过\(2B\)行通过排列组合以及中位数和平均数推断出三位公民的年龄大致处于

总结反思

• 虽然发动聚合裂解攻击都是一个\(NP\)难问题，但是通过人工启发式的做法就能排除掉大部分的无效数据
• 同理这种攻击在美国2010年人口普查中足以重构出\(46%\)的人口的小数据，同时对于\(71\)的人口，其误差不大于一年。通过一些附加的商业数据集，可以重新辨别出\(50\)万人的姓名

查询（Queries），全然非隐私（BNP）以及Dinur-Nissim攻击

从这里开始严谨完备地定义我们的模型。

• 给定一个带有几个数据（points）的列表
  • 首先定义每一个数据为行（rows）
  • 定义特征或者说每条数据的维度为列（columns）
  • 有一些特征为唯一标识符，例如说名字，邮政编码以及出生年月日和性别等，这里的标识符都是完全公开的
  • 其中一个二进制位特征作为使用的隐私符号
  • 其中\(d\in \{0,1\}^n\)为隐私符的向量

模型架构

对于一个数据分析器（Data analyst）会对列表执行一系列的查询（Queries），而且一个管理者（Curator）则通过手段去保护数据集中每个人的隐私

对于一个具体的数据分析器有能力去询问有多少符合条件的人其隐私码为\(1\)，例如说：“叫作爱丽丝或者查理再或者戴维”的查询结果为\(2\)。

再一步抽象起见，一个数据分析器有能力给出一个向量来查询指定的人，例如说给出一个向量\(S\in\{0,1\}^n\)，其中的\(1\)为欲查询的个人而\(0\)为非查询的个人。称为子集查询（Subset queries），这种指定查询可能会异常复杂，但是我们暂且避之不谈，当然后面关于Cohen-Nissim攻击的部分会提到他。

对于查询\(S\)数学表述：

\[A(S) = d \cdot S
\]

当管理者接受到一个查询集\(S\)，然后就会返回一个响应（response），称为\(r(S)\)。也就是说整个流程简化为：

\[r(S)=A(S)
\]

当然这意味着就会极易造成侵犯隐私，为此分析器只能执行当个查询\(S=\{i\}\)，以揭示某个人\(i\)的隐私符。

理所当然，管理者会输出一个带噪音的\(A(S)\)：具体来说，就是输出一个\(r(S)\)，其中\(r(S)\)对于某个界限\(E\)，符合\(|r(S)-A(S)|\le E\)。留意到其差值\(r(S)-A(S)\)并不一定是随机分布的，而管理者可能输出符合与\(A(S)\)存在距离\(E\)的\(r(S)\)

定义（1）

若一个算法是完全非隐私（Blatantly Non-Private，缩写为\(BNP\)），那么攻击者将可以重建一个数据库\(c\in \{0,1\}^n\)，与真正数据库\(d\)完全匹配，而未能识别的条目数量为\(o(n)\)。

如果一个算法是\(BNP\)的，那么这个算法之下毫无隐私可言。这就是重构攻击（reconstruction attack），随后我们可以证明出一般的方案都是\(BNP\)

定理（2）

如果一个分析器可以访问\(2^n\)次的子集查询，而管理者可以加入界限\(E\)的噪音。那么攻击者有能力重构整个数据库，只不过带了\(4E\)的偏移

尤其当\(E=n/401\)，攻击者就能复原出$99 % \(准确的数据库。也就是说，当\)E=o(n)\(，则该算法属于\)BNP$

定理证明：

假设攻击者发动了\(2^n\)次询问，也就是说其能输出查找所有可能的数据库查询组合\(S\)。随后我们遍历所有待定的数据库\(c\in \{0,1\}^n\)，滤掉所有\(|\sum_{i\in S}c_i -r(S)|\le E\)的\(c\)。然后输出符合的\(c\)。

定理（3）

若数据分析有能力进行\(O(n)\)次子集查询，并且管理者会加入\(E=O(\alpha\sqrt n)\)的界限的噪音。那么一个计算高效的攻击者可以重构一个有\(O(\alpha^2)\)偏移的数据库

总结

• 第一种攻击需要\(2^n\)次的查询以消除\(O(n)\)的噪音
• 第二种攻击需要\(\Omega(n)\)次的查询以消除\(O(\sqrt n)\)的噪音（还有加强版本）

而差分隐私允许进行\(O(n)\)次查询的同时增加总模长为\(O(\sqrt n)\)的噪音，一般是通过拉普拉斯或者高斯机制去实现。

一般来说，如果数据分析仅请求\(m<<n\)次的查询，那么管理者只需要增加总模长为\(O(\sqrt{(m)})\)的噪音。