[TAD] Triangles of Absolute Differences-反帕斯卡三角形

[IMO2018] Triangles of Absolute Differences-反帕斯卡三角形

前言 叠甲

笔者不是学数竞的，在此感谢我的数竞生为我讲解题目。

笔者学艺不精，且知识面浅薄。

所以本文章仅用作搞抽象 (争取练就惊人注意力 。

正文

一、引入

看完这道题目的要求，相信大家都能想起一个很熟悉的东西：

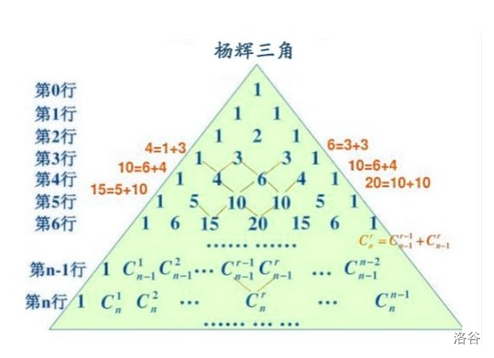
杨辉三角形

杨辉三角(帕斯卡三角形)，是二项式系数在三角形中的一种几何排列，中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。它把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合。

由于杨辉三角的特殊性质，我们可以从中直观地得出二项式定理：

\[\small
(x+a)^n = \sum_{k=0}^{n} C_n^ka^{n-k} b^k
\]

帕斯卡三角形是上面的数等于下面的数之和，反帕斯卡三角形是上面的数等于下面的数之差，

两者概念十分的相似，那么我们就很好地理解了反帕斯卡三角形是个什么东西。

显然以上内容与本题无关。

二、证明思路

1、性感理解（？）

问题为是否存在一个 \(n\) 行的反帕斯卡三角形，即该三角形中包含 \(1\sim \frac {n\times(n+1)}{2}\) 中所有的整数。

首先可以列举出一些较为简单的情况：

通过观察简单情况以及直观感受，我们发现：

似乎那些 “看起来小一些的数” 多在三角形顶部，“看起来大一点的数” 多在三角形底部。

那么对于一般性问题，我们可以基于这些 “没什么道理但十分直观的感受” 进行思考。

• 考虑如果存在一个为 \(n\) 行的反帕斯卡三角形（最终希望产生矛盾），那么其一定会包含一些 “较小的数” 和 “较大的数” 。

那么接下来的工作重点就来到了：

1. “较大”与“较小”该如何定义；
2. 这些数都有哪些可以被我们利用的性质。

2、“较大”与“较小”数的定义

设一个有 \(n\) 行的反帕斯卡三角形中：

• 第 \(i\) 行最大的数为 \(mx_i\)，最小的数为 \(mn_{i}(1\le i\le n)\)，且有 \(mx_1==mn_1\)。

考虑 \(mx_i(1\le i\le n-1)\) 下方的两个数分别为 \(d\) 和 \(r\)：

\[\small
\begin{aligned}
\because\space &mx_i = |d - r| \le mx_{i+1}- mn_{i+1} \\
\therefore\space &mx_{i+1}-mx_i \ge mn_{i+1} \\
\because\space &\sum_{i=1}^{n-1}(mx_{i+1}-mx_i)\ge\sum_{i=1}^{n-1}{mn}_{i+1} \\
\therefore\space &mx_1+\sum_{i=1}^{n-1}mn_{i+1} \le mx_n \\
\therefore\space &\sum_{i=1}^{n}mn_i \le mx_n\\
\end{aligned}
\]

最后的结论如果仅凭自己的直观感受，貌似是显然易见的，但这与 “较大”“较小”的数有何关系呢？

\[\small
\begin{aligned}
\because\space &mn_i\space为每一行中最小的数 \\
\therefore\space &\sum_{i=1}^n {mn}_i \ge \sum_{i=1}^n i\\
\therefore\space &\sum_{i=1}^ni \le {mx}_n\\
\because\space &mx_n \ge \sum_{i=1}^{n} i\\
\therefore\space &mx_n=\sum_{i=1}^ni=\frac {n\times(n+1)}{2}\\
\therefore\space &\sum_{i=1}^n{mn}_i = \sum_{i=1}^n i\\
\therefore\space &mn \in{[1,n]}\\
\therefore\space &整数\space1\sim n\space恰分布在三角形的每一行中，\\
&且为每一行中最小的数\\
\end{aligned}
\]

到此，我们就证明了 \(1\sim n\) 存在于三角形的每一行中，并且为每一行中“最小的数”。回看我们所列举的几个三角形，发现它们都满足这个条件。

并且，由于在三角形中，靠近顶部的数字较少，靠近底部的数字较多，且最大的数在三角形的最底部，所以带给了我们一种

似乎那些 “看起来小一些的数” 多在三角形顶部，“看起来大一点的数” 多在三角形底部

的 (惊人注意力 直观感受。

既然 \(1\sim n\) 在每一行都有且是三角形中最小的数字，那么在一个有 \(n\) 行的反帕斯卡三角形中，不妨：

• 令 \(sml\) 表示那些 “较小的数” ，且 \(1\le sml \le n\)；
• 对称的，令 \(lag\) 表示那些 “较大的数” ，且 \(\frac {n\times(n+1)}{2}-n\le lag \le\frac {n\times(n+1)}{2}\);

3、“较大”与“较小”数的性质

“较小的数”的性质

1. 数 \(1\sim n\) 存在于三角形的每一行中，并且为每一行中 “最小的数” 。

“较大的数”的性质

1. 对于“较大的数”的分布，我们只能确定第 \(n\) 行的 “最大的数” 为 \(\frac {n\times(n+1)}{2}\)，而无法确定每行中存在的 “较大的数” 是否唯一。

2. 对于两个互异的“较大的数 \(lag_x\) 和 \(lag_y\)，其差的绝对值一定为一个 “较小的数”。

\[\small
\begin{aligned}
\because\space &\frac {n\times(n+1)}{2}-n\le lag \le\frac {n\times(n+1)}{2} \\
\therefore\space &1\le |lag_x-lag_y| \le n
\end{aligned}
\]

1. 除第 \(n\) 行的“较大的数”外，其余行的“较大的数”都是由 一个“较大的数”与一个“较小的数” 相减得到的。

\[\small
\begin{aligned}
\because\space &1\le sml \le n \\
\therefore\space &1\le |sml_x-sml_y| \le n-1 \\
\because\space &存在“较大的数”性质 \space2\\
\therefore\space &lag_x = lag_y-sml_y
\end{aligned}
\]

1. 第 \(n\) 行最多有两个“较大的数”相邻。

\[\small
\begin{aligned}
假&设第\space n\space行存在\space K\space个“较大的数”相邻\\
由&“较大的数”性质\space2\space可知：第\space n-1\space行存在\space K-1\space个“较小的数”\\
\because\space &存在“较小的数”性质 \space1 \\
\therefore\space &K-1=1\\
\therefore\space &K=2
\end{aligned}
\]

1. 第 \(n\) 行最多存在 \(1+\lfloor n/2 \rfloor\) 个“较大的数”（每两个“较大的数”之间必有一个“较小的数”隔开）。

\[\small
\begin{aligned}
\because\space &存在“较大的数”性质\space4 \\
&且第\space n\space行共有\space n\space个数 \\
\therefore\space &第\space n\space行最多存在\space 1+\lfloor n/2 \rfloor\space个“较大的数”
\end{aligned}
\]

4、最后开始解题

显然有一个性质：总存在第 \(n-T+1\) 行，使得第 \(1 \sim n-T\) 行都不存在“较大的数”。

我们在前面“较大的数”五条性质的基础上，希望探究 \(T\) 可能存在的性质，以此来推出矛盾完成题目。

我们发现了很多关于 \(n\) 的性质，所以考虑把 \(T\) 与 \(n\) 扯上关系。

我们先来寻找 \(mx_{n-T+1}\) 的边界。

\[\small
\begin{aligned}
下&界我们是知道的：mx_{n-T+1} \ge lag_{min} = \frac {n\times(n+1)}{2}-n \\
上&界考虑“局部累加”: \\
\because\space &mn_i \le mx_i-mx_{i-1}\\
\therefore\space &\sum_{i=n-T+2}^{n} mn_i \le \sum_{i=n}^{n-T+2}{mx_i-mx_{i-1}} = mx_n-mx_{n-T+1}\\
\therefore\space &{mx}_{n-T+1} \le {mx}_n - \sum_{i=n-T+2}^{n}{mn}_i\\
\because\space &\sum_{i=n-T+2}^{n}{mn}_i \ge \sum_{i=1}^{T-1}i\\
&且\space mx_n = \frac {n\times(n+1)}{2}\\
\therefore\space &{mx}_{n-T+1} \le \frac {n\times(n+1)}{2} - \frac {T\times(T-1)}{2}
\end{aligned}
\]

发现在 \(mx_{n-T+1}\) 的上界中 \(T\) 与 \(n\) 有关系。

然后，我们再来寻找 \(T\) 的范围：

\[\small
\begin{aligned}
\because\space &第 \space n \space行最多存在\space 1+\lfloor n/2 \rfloor\space个“较大的数”\\
&且存在“较大的数”性质\space 3\space以及“较小的数”性质\\
\therefore\space &第\space n-1 \space行最多存在\space 2 \space个“较大的数”\\
&且如果有\space 2\space个“较大的数”则其必相邻\\
\therefore\space &第\space n-2 \space行最多存在1个“较大的数”\\
\therefore\space &第\space 1\sim n-T+2 \space行每行都最多存在\space 1\space个“较大的数”\\
\because\space &“较大的数”共有\space n+1 \space个\\
\therefore\space &n+1 \le (1+\lfloor n/2 \rfloor) +2+(T-2)\times 1\\
\therefore\space &T \ge n-\lfloor n/2 \rfloor
\end{aligned}
\]

此时，\(T\) 的下界与 \(n\) 有关系。

所以我们希望通过 \(mx_{n-T+1}\) 与 \(T\) 推出矛盾。

\[\small
\begin{aligned}
当&\space n = 2018\space 时，T\ge1009\\
\because\space &{mx}_{n-T+1} \le \frac {n\times(n+1)}{2} - \frac {T\times(T-1)}{2}\\
\therefore\space &{mx}_{2019-T} \le \frac {2018\times2019}{2} - \frac {T\times(T-1)}{2}\\
\therefore\space &{mx}_{2019-T} \le \frac {2018\times2019}{2} - \frac {1009\times(1008)}{2} = 1528635\\
\because\space &mx_{n-T+1} \ge \frac {n\times(n+1)}{2}-n \\
\therefore\space &mx_{2019-T} \ge {2018\times(2019)}{2} - 2018 = 2035153\\
发&现此时推出了关于\space mx_{2019-T}\space的矛盾\\
那&么当\space n=2018\space时就不存在反帕斯卡三角形
\end{aligned}
\]

5、思考题目的边界

容易想到一定存在一个 \(n\) 使得不存在大于 \(n\) 行的反帕斯卡三角形。

也就是说，我们所能证明的边界是对于 \(mx_{n-T+1}\) 恰好无法推出矛盾，即求：

\[\small
\begin{aligned}
&\frac {n\times(n+1)}{2}-n \le \frac {n\times(n+1)}{2} - \frac {T\times(T-1)}{2}\space的最大整数解\\
\because\space &T \ge n-\lfloor n/2 \rfloor\\
\therefore\space &求：\frac {n\times(n+1)}{2}-n \le \frac {n\times(n+1)}{2} - \frac {(n-\lfloor n/2 \rfloor)\times(n-\lfloor n/2 \rfloor-1)}{2} \space的最大整数解\\
&解得：n = 8
\end{aligned}
\]

也就是说，我们用前面的方法可以证明当 \(n>8\) 时，不存在有 \(n\) 行的反帕斯卡三角形。

后记

我们的方法只能证明 \(n>8\) 时不存在有 \(n\) 行的反帕斯卡三角形，总之是可以做对这道题目。

但其实当 \(6\le n\) 是，就不存在有 \(n\) 行的反帕斯卡三角形了。

具体证明大家可以看两篇论文：

1. Triangles of Absolute Differences 基于树形结构证明
2. 1977 Exact Difference Triangles 完美的 \(n\) 阶反帕斯卡三角形

于是文章到这就没了，我也不知道自己在干些什么。