Word2vector原理

词向量：

用一个向量的形式表示一个词

词向量的一种表示方式是one-hot的表示形式：首先，统计出语料中的所有词汇，然后对每个词汇编号，针对每个词建立V维的向量，向量的每个维度表示一个词，所以，对应编号位置上的维度数值为1，其他维度全为0。这种方式存在问题并且引发新的质疑：1）无法衡量相关词之间的距离  2）V维表示语义空间是否有必要

词向量获取方式：

1）基于奇异值分解的方法

a、单词－文档矩阵

基于的假设：相关词往往出现在同一文档中，例如，banks 和 bonds, stocks,money 更相关且常出现在一篇文档中，而 banks 和 octous, banana, hockey 不太可能同时出现在一起。因此，可以建立词和文档的矩阵，通过对此矩阵做奇异值分解，可以获取词的向量表示。

b、单词－单词矩阵

基于的假设：一个词的含义由上下文信息决定，那么两个词之间的上下文相似，是否可推测二者非常相似。设定上下文窗口，统计建立词和词之间的共现矩阵，通过对矩阵做奇异值分解获得词向量。

2）基于迭代的方法

目前基于迭代的方法获取词向量大多是基于语言模型的训练得到的，对于一个合理的句子，希望语言模型能够给予一个较大的概率，同理，对于一个不合理的句子，给予较小的概率评估。具体的形式化表示如下：

 

 

第一个公式：一元语言模型，假设当前词的概率只和自己有关；第二个公式：二元语言模型，假设当前词的概率和前一个词有关。那么问题来了，如何从语料库中学习给定上下文预测当前词的概率值呢？

a、Continuous Bag of Words Model（CBOW）

给定上下文预测目标词的概率分布，例如，给定｛The，cat，()，over，the，puddle｝预测中心词是jumped的概率，模型的结构如下：

 

如何训练该模型呢？首先定义目标函数，随后通过梯度下降法，优化此神经网络。目标函数可以采用交叉熵函数：

 

由于yj是one－hot的表示方式，只有当yj＝i 时，目标函数才不为0，因此，目标函数变为：

 

代入预测值的计算公式，目标函数可转化为：

 

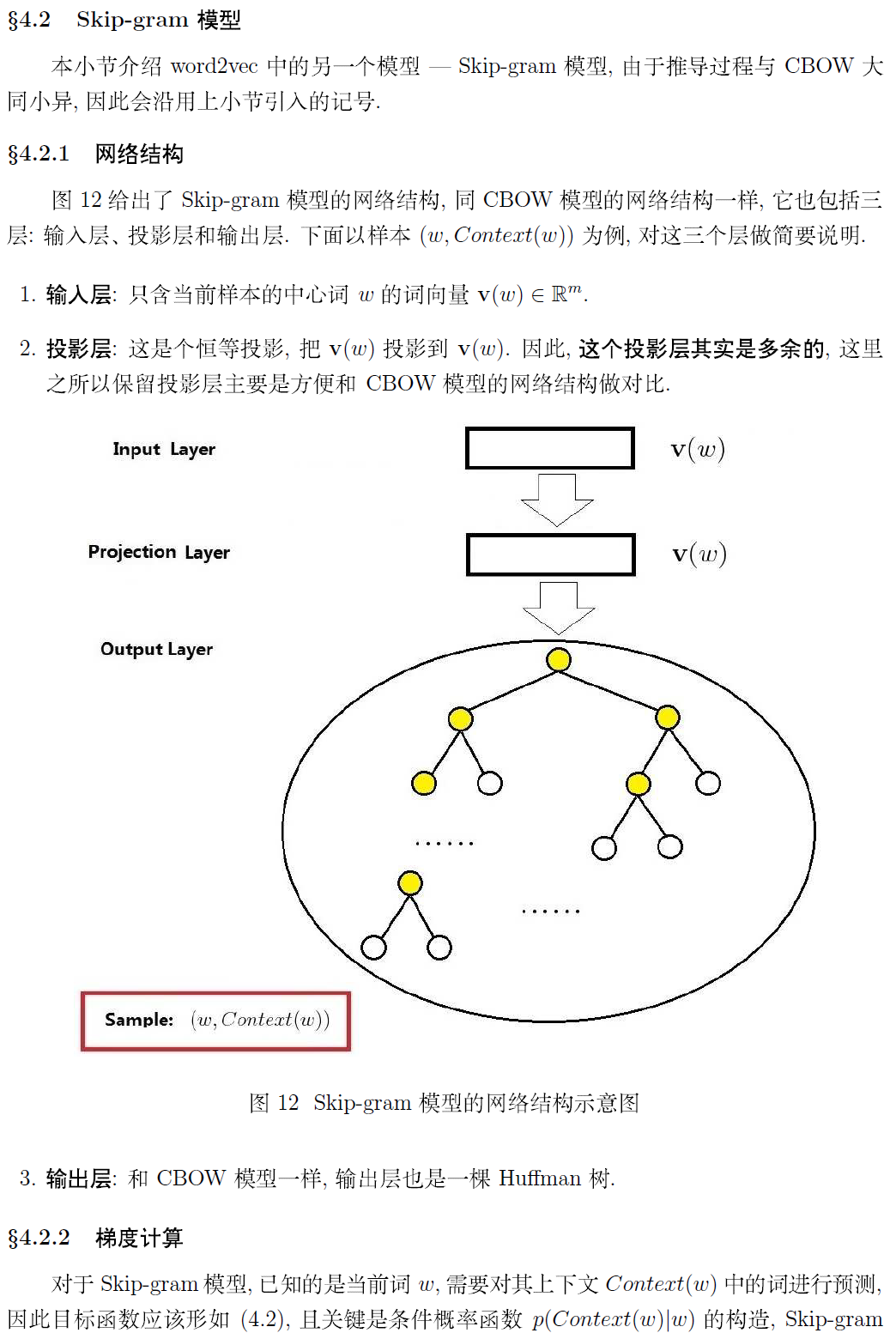
b、Skip-Gram Model

skip－gram模型是给定目标词预测上下文的概率值，模型的结构如下：

 

同理，对于skip－ngram模型也需要设定一个目标函数，随后采用优化方法找到该model的最佳参数解，目标函数如下：

 

分析上述model发现，预概率时的softmax操作，需要计算隐藏层和输出层所有V中单词之间的概率，这是一个非常耗时的操作，因此，为了优化模型的训练，minkov文中提到Hierarchical softmax 和 Negative sampling 两种方法对上述模型进行训练，具体详细的推导可以参考文献1和文献2。

---

word2vec中用到两个重要模型：CBOW模型和Skip-gram模型。

两个模型都包含三层：输入层、投影层和输出层。前者是在已知当前词$W_t$的上下文$W_{t-2}, W_{t-1}, W_{t+1}, W_{t+2}$的前提下预测当前词$W_t$, 而后者是在已知当前词$W_t$的前提下，预测其上下文$W_{t-2},  W_{t-1}, W_{t+1}, W_{t+2}$ 。

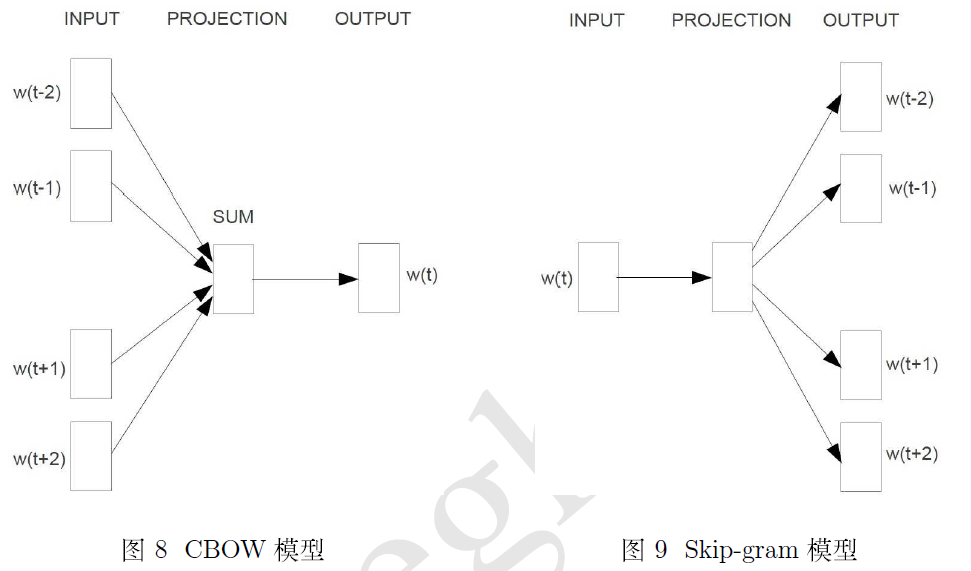
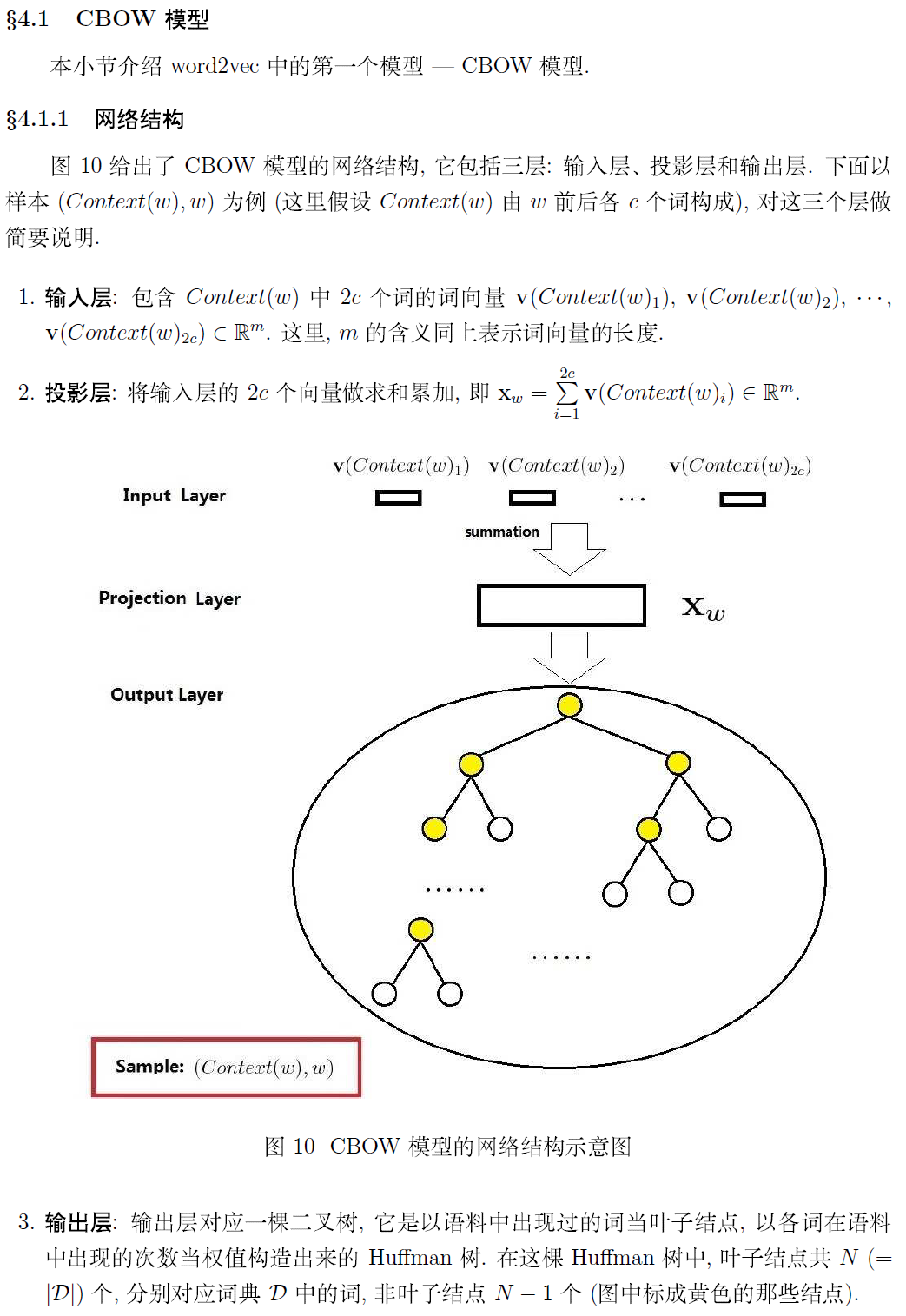
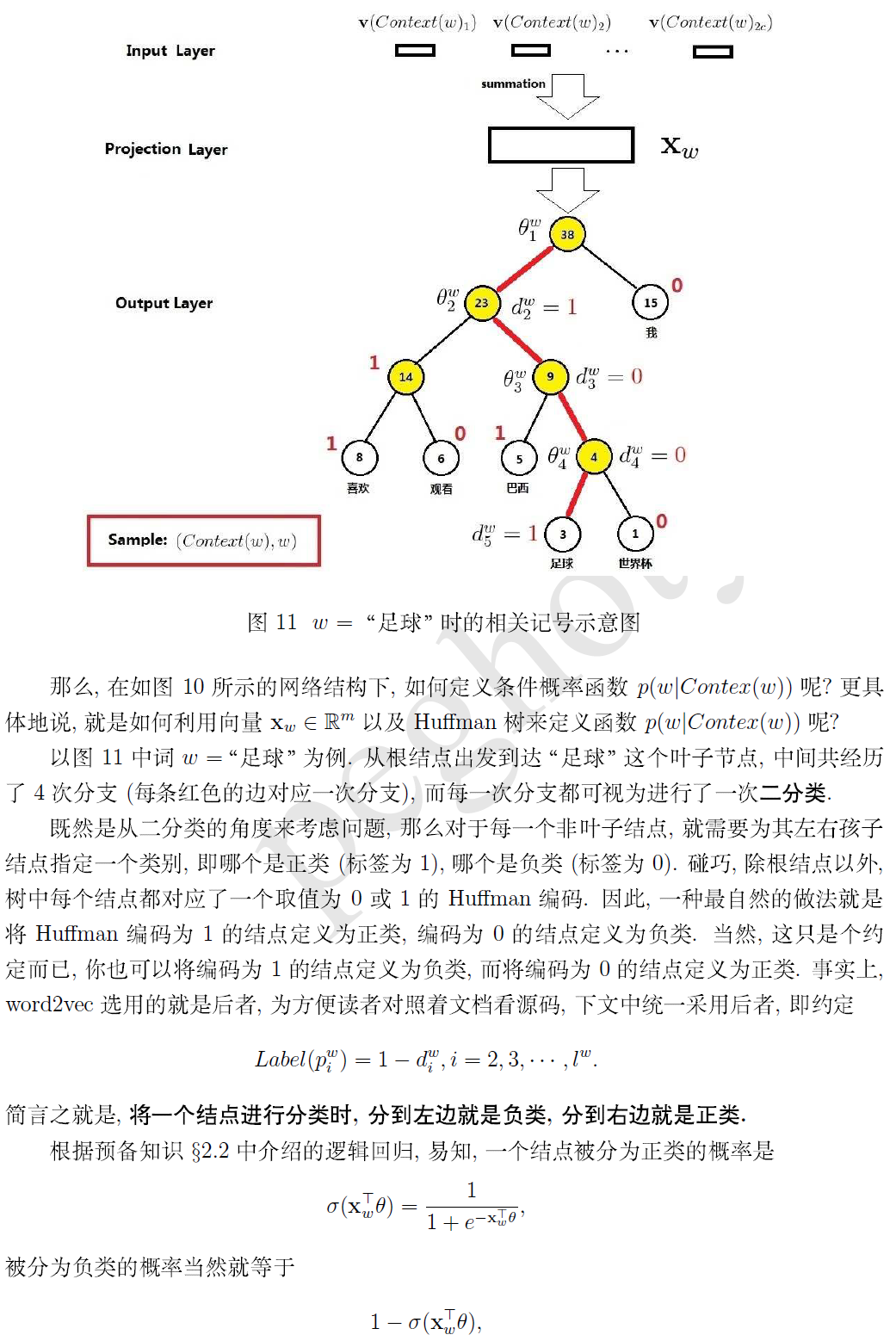
对于CBOW和Skip-gram两个模型，Word2Vec给出了两套框架，它们分别基于Hier-archical Softmax 和Negative Sampling来进行设计。本文介绍基于Hierarchical Softmax的CBOW和Skip-gram模型。

 

 

 

 

 

 

参考：

http://www.jianshu.com/p/b2da4d94a122

http://blog.csdn.net/itplus/article/details/37969979

http://blog.csdn.net/zhoubl668/article/details/24314769