BZOJ4561：圆的异或并（扫描线+set||splay||线段树）

在平面直角坐标系中给定N个圆。已知这些圆两两没有交点，即两圆的关系只存在相离和包含。求这些圆的异或面

   积并。异或面积并为：当一片区域在奇数个圆内则计算其面积，当一片区域在偶数个圆内则不考虑。

Input

第一行包含一个正整数N，代表圆的个数。接下来N行，每行3个非负整数x,y,r，表示一个圆心在(x,y)，半径为r的

圆。保证|x|,|y|,≤10^8，r>0,N<=200000

Output

仅一行一个整数，表示所有圆的异或面积并除以圆周率Pi的结果。

Sample Input

  2

  0 0 1

  0 0 2

Sample Output

3

思路：扫描线，有很多这样的题，思路就是分成上下两半圆，然后用数据结构。

前提是不相交。然后可以求出包含关系。

具体：把一个圆分为上下两个半圆，然后每次扫描线扫到一个圆X（左边），去找这个圆的“上面的第一个半圆Cir”，若Cir是上半圆的话，则X被其包含，否则无。                     然后把圆X加入数据结构中。

扫描到一个圆X（右边），则把圆X从数据结构中删除。

对于当前扫描线里的圆（保存在数据结构里的那些），排序是根据直线与圆的交点的纵坐标排序得到：

下面左图，B上面第一个圆是A，因为3上面第一个点是2。而2代表下半圆，说明无圆包含B。

下图右图，B上面第一个圆是A，因为3上面第一个点是1。而1代表上半圆，说明第一个包含B的是A。（可能A还被其他圆包含，即B<A<...）

简单证明划分圆来解决的可行性：

由于圆之间不相交，所以我们用平行Y轴是直线去扫描的时候（从左向右），直线与圆产生一些交点。

易得：这些圆中，一个圆与直线的两个交点与其他圆的两个交点不交叉。即一对交点“属于哪个圆”这个属性“相离”或者“包含”，不会“交叉”，如下：

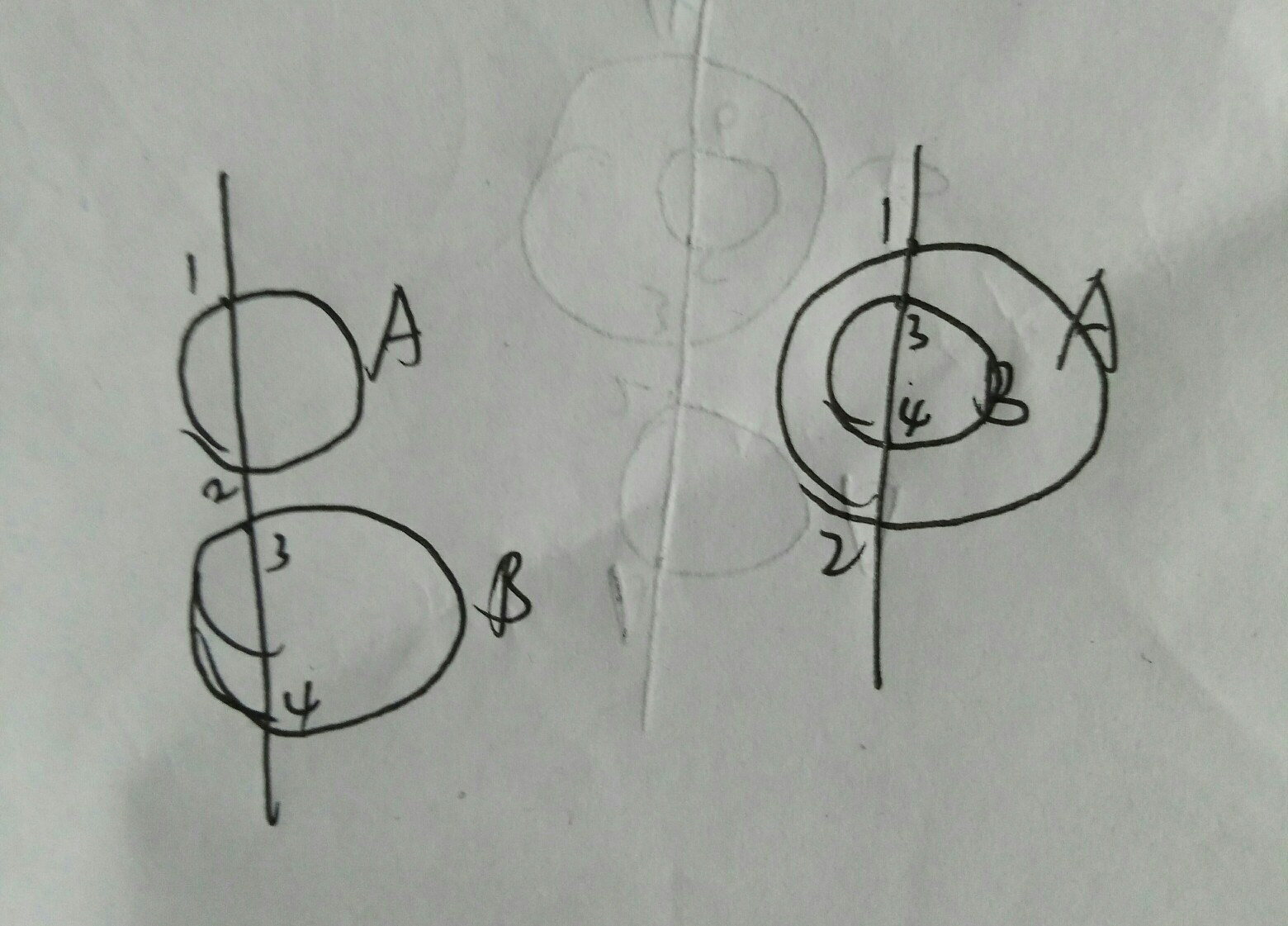
如左图：A圆与直线交点1，2，B圆与直线交点3，4。二圆相离，所以（1，2），（3，4）。

如右图：A圆与直线交点1，2，B圆与直线交点3，4。二圆包含。所以（1，（3，4）2）。

不会出现下图中的（1，（3，2）4）

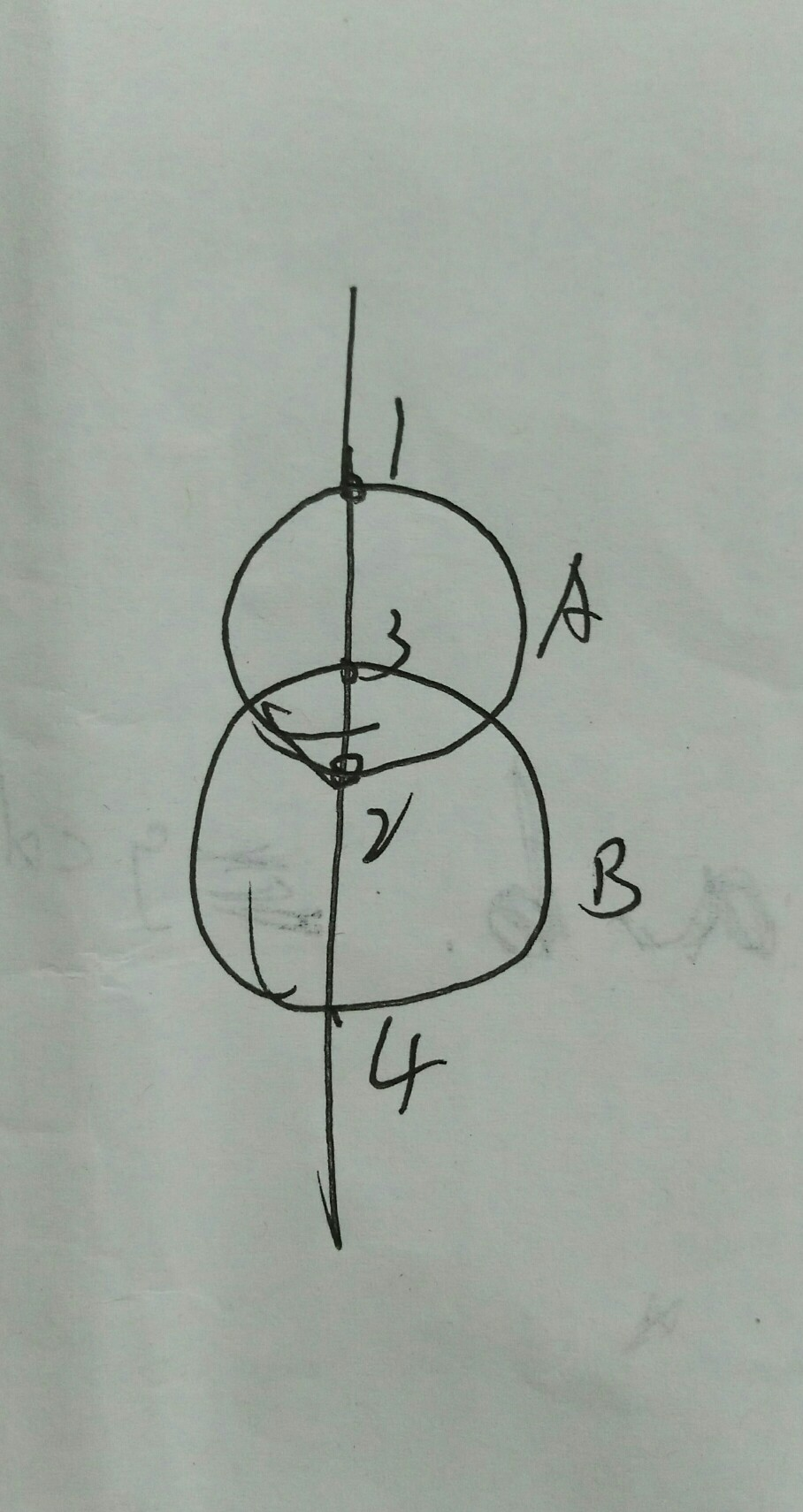
因此，一个圆X被圆Y包含，要求最内层的Y，只需要在这条线上找X与直线的交点a上面的第一个“下半圆交点”即可。

-----------------------上面是简单证明，下面是整正题--------------------------

数据结构用于查找大于等于a的数，可以是set，线段树，判平衡树等。

这里是练习平衡树，但是为了保险，先写了下set，不然直接写splay找错很麻烦。

待续。。。。

#include<set>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
using namespace std;
#define ll long long
const int maxn=;
struct cir{
     ll x,y,r;
     cir(){}
     cir(ll xx,ll yy,ll rr):x(xx),y(yy),r(rr){}
}c[maxn];
struct ins{
     int x,opt,id;
     ins(){}
     ins(int xx,int oo,int ii):x(xx),opt(oo),id(ii){}
}w[maxn<<];=
ll Lx,sig[maxn];  set<ins>s;
ll cal(ll x) { return x*x; }
bool cmp(ins a,ins b){ return a.x<b.x; }
bool operator <(ins a,ins b){

    double y1=c[a.id].y+a.opt*sqrt(cal(c[a.id].r)-cal(c[a.id].x-Lx));
    double y2=c[b.id].y+b.opt*sqrt(cal(c[b.id].r)-cal(c[b.id].x-Lx));
    if(y1==y2) return a.opt<b.opt; //当一个圆的左顶点刚好在LX线上？
    return y1<y2;
}
int main()
{
    int N; scanf("%d",&N);
    for(int i=;i<=N;i++){
        scanf("%lld%lld%lld",&c[i].x,&c[i].y,&c[i].r);
        w[(i<<)-]=ins(c[i].x-c[i].r,,i);
        w[i<<]=ins(c[i].x+c[i].r,-,i);
    }
    sort(w+,w+(N<<)+,cmp);
    for(int i=;i<=(N<<);i++){
        Lx=w[i].x;
        if(w[i].opt==){//左，加圆 

            set<ins>::iterator it;
            it=s.upper_bound(ins(,,w[i].id));
            if(it==s.end()) sig[w[i].id]=;
            else{
                if((*it).opt==-) sig[w[i].id]=sig[(*it).id];
                else sig[w[i].id]=-sig[(*it).id];
            }
            s.insert(ins(,,w[i].id));
            s.insert(ins(,-,w[i].id));
        }
        else {
            s.erase(ins(,,w[i].id));
            s.erase(ins(,-,w[i].id));
        }
    }
    ll ans=;
    for(int i=;i<=N;i++)  ans+=sig[i]*cal(c[i].r);
    printf("%lld\n",ans);
    return ;
}