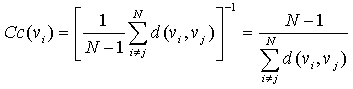社交网络图中结点的“重要性”计算 (30 分) C++解法
社交网络图中结点的“重要性”计算 (30 分)
在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来。他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用,可以增强也可以减弱。而结点根据其所处的位置不同,其在网络中体现的重要性也不尽相同。
“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标,即一个有较高中心性的结点比有较低中心性的结点能够更快地(平均意义下)到达网络中的其它结点,因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中,结点vi 的“紧密度中心性”Cc(vi )数学上定义为vi 到其余所有结点vj (j≠i) 的最短距离d(vi ,vj )的平均值的倒数:
对于非连通图,所有结点的紧密度中心性都是0。
给定一个无权的无向图以及其中的一组结点,计算这组结点中每个结点的紧密度中心性。
输入格式:
输入第一行给出两个正整数N和M,其中N(≤104 )是图中结点个数,顺便假设结点从1到N编号;M(≤105 )是边的条数。随后的M行中,每行给出一条边的信息,即该边连接的两个结点编号,中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K(≤100)以及K个结点编号,用空格分隔。
输出格式:
按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性,每个输出占一行,结果保留到小数点后2位。
输入样例:
9 14
1 2
1 3
1 4
2 3
3 4
4 5
4 6
5 6
5 7
5 8
6 7
6 8
7 8
7 9
3 3 4 9
输出样例:
Cc(3)=0.47
Cc(4)=0.62
Cc(9)=0.35
代码:
#include <iostream>
#include <queue>
#include <climits>
#include <map>
using namespace std;
class Graph {
public:
Graph(int v, int e) : Vertex(v), Edge(e) {
G = new int *[v];
for (int i = 0; i < v; i++) {
G[i] = new int[v];
for (int j = 0; j < v; j++) {
G[i][j] = 0;
}
}
}
~Graph(){
for (int i = 0; i < Vertex; i++) {
delete[] G[i];
}
delete[] G;
}
void Insert(int v1, int v2) {
G[v1][v2] = 1;
G[v2][v1] = 1;
}
double Importance(int v) {
int distance[Vertex];
for (int i = 0; i < Vertex; i++) {
distance[i] = INT_MAX;
}
distance[v] = 0;
int Visited[Vertex][Vertex];
for (int i = 0; i < Vertex; i++) {
for (int j = 0; j < Vertex; j++) {
Visited[i][j] = 0;
}
}
map<int,int> visitedNode;
queue<int> q;
q.push(v);
while (!q.empty()) {
int temp = q.front();
q.pop();
for (int i = 0; i < Vertex; i++) {
if (G[temp][i] == 1 && Visited[temp][i] == 0 && visitedNode[i]==0) {
if (distance[i] > distance[temp] + 1)
distance[i] = distance[temp] + 1;
visitedNode[i]=1;
q.push(i);
Visited[temp][i] = 1;
Visited[i][temp] = 1;
}
}
}
double sum = 0;
for (int i = 0; i < Vertex; i++) {
sum += distance[i];
}
return (Vertex - 1.0) / sum;
}
private:
int Vertex;
int Edge;
int **G;
};
int main() {
int vertex, edge;
scanf("%d %d", &vertex, &edge);
Graph graph(vertex, edge);
int temp1, temp2;
for (int i = 0; i < edge; i++) {
scanf("%d %d", &temp1, &temp2);
graph.Insert(temp1 - 1, temp2 - 1);
}
int num;
scanf("%d", &num);
int n;
for (int i = 0; i < num; i++) {
scanf("%d", &n);
printf("Cc(%d)=%.2f\n", n, graph.Importance(n - 1));
}
}
社交网络图中结点的“重要性”计算 (30 分) C++解法的更多相关文章
- PTA数据结构与算法题目集(中文) 7-36 社交网络图中结点的“重要性”计算 (30 分)
PTA数据结构与算法题目集(中文) 7-36 社交网络图中结点的“重要性”计算 (30 分) 7-36 社交网络图中结点的“重要性”计算 (30 分) 在社交网络中,个人或单位(结点)之间通过某 ...
- PTA 社交网络图中结点的“重要性”计算(30 分)
7-12 社交网络图中结点的“重要性”计算(30 分) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互 ...
- 7-10 社交网络图中结点的“重要性”计算(30 point(s)) 【并查集+BFS】
7-10 社交网络图中结点的"重要性"计算(30 point(s)) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络 ...
- PTA 7-12(图) 社交网络图中结点的“重要性”计算 最短路
7-12(图) 社交网络图中结点的“重要性”计算 (30 分) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的 ...
- 7-11 社交网络图中结点的“重要性”计算 (30 分)(Dijkstra算法)
题意: 思路:对每个输入的点跑一遍dijkstra算法,然后对这个点到所有点的距离求和按公式输出就可以了. (这次尝试了用数组模拟链表来做最短路问题,刷新了自己对最短路的理解) 这里构造链表的过程我 ...
- Excel中最精确的计算年龄的公式
身份证算年龄 假设A1是身份证号所在单元格 =IF(MONTH(NOW())<INT(MID(A1,11,2)),INT(YEAR(NOW())-INT(MID(A1,7,4)))-1,IF(M ...
- sql server2005版本中,len函数计算了字符串末尾的空格
sql server2005版本中,len函数计算了字符串末尾的空格的长度,以下是测试脚本: print @@version declare @v varchar(max) set @v = 'hp, ...
- dgraph解决社交关系中的正反向查找
dgraph解决社交关系中的正反向查找 本篇介绍的是, 社交关系中的关注者与被关注者在dgraph中如何实现查找. 对dgraph的基本操作不太清楚的可以看看我之前写的博客 dgraph实现基本操作 ...
- jQuery中height()不能精确计算的问题
jQuery中关于高度的计算有三个方法:outerHeight().innerHeight().height() outerHeight():获取元素集合中第一个元素的当前计算高度值,包括paddin ...
随机推荐
- iOS动画案例(1) 仿qq账号信息里的一个动画
受人所托,模仿qq账号信息里的一个动画,感觉挺有意思,也没感觉有多难,就开始做了,结果才发现学的数学知识都还给体育老师了,研究了大半天才做出来. 先看一下动画效果: 用到的知识点: ( ...
- jeasyUI treegrid 的 reload 和 getChanges
看上去,treegrid继承自datagrid,因此,datagrid有的,treegrid也会有. 比如说,getChanges,翻看那些网络教程,绝大多数都没提treegrid有这个东东.但是,t ...
- c# Custom Controls
http://www.cnblogs.com/light169/archive/2008/06/11/1217139.html
- frame pointer及其用途
1 什么是frame pointer frame pointer指向本函数栈帧顶,通过它可以找到本函数在进程栈中的位置.有专门的寄存器保存该值. 2 frame pointer有什么用 主要是back ...
- golang中管道热替换
golang中管道替换问题 https://blog.csdn.net/cyk2396/article/details/78875347 1.运行以下代码: var chan1 chan int va ...
- 杂项-DB:Druid
ylbtech-杂项-DB:Druid Apache Druid (incubating) is a high performance analytics data store for event-d ...
- GCD中各种队列和任务执行方式的组合
一.概念回顾 1.GCD全称 Grand Central Dispatch ,是纯C语言,提供了非常多强大的函数,来进行系统线程的管理. 2.优势:GCD是苹果公司为多核的并行运算提出的解决方案.GC ...
- LVS的持久连接、会话保持和高可用介绍
持续连接 1)持久连接(lvs persistence)模板: 实现无论使用任何调度算法,在一段时间内(默认360s),能够实现将来自同一个地址的请求始终发往同一个RS ipvsadm -A|E -t ...
- Web Api之Cors跨域(干货)---大家一定要看清我写的内容哦
Web Api之Cors跨域 要想跨域需要准备一下几步骤 1.创建WebAPI(请按照图片先后顺序来) 2.进入NuGet包管理搜 Microsoft.AspNet.WebApi.Cors 进行下载 ...
- view 的继承关系
view 的继承关系 如果一个view 有多个子view. 甚至是多成次的 子view. 只需要把第一级别的view(父view) 授权给用户,就可以访问view了,子view 不需要授权.