【6.24校内test】T1 江城唱晚

【题目背景】

墙角那株海棠，是你种下的思念。

生死不能忘，高烛照容颜。

一曲江城唱晚，重忆当年坐灯前，

青衫中绣着你留下的线。

——银临《江城唱晚》

【问题描述】

扶苏是个喜欢一边听古风歌一边写数学题的人，所以这道题其实是五三原题。

歌曲中的主人公看着墙边的海棠花，想起当年他其实和自己沿着墙边种了一排海 棠，但是如今都已枯萎，只剩下那一株，寄托着对他深深的思念。

沿着墙一共有 n 个位置可以种下海棠花，主人公记得自己当年和他一共种下了 m 朵，由于花的特性，海棠不能紧挨着种植，也就是两朵海棠花之间最少间隔一个不种花 的空位置。但是她记不清当时海棠花具体是怎么摆放的了，所以她想知道一共有多少方 案使得 m 朵海棠花都被种下且两两之间不是相邻的。我们将这 m 朵海棠花按照 1,2,3…m 的顺序编号，两个种花的方案不同当且仅当它们被种下的位置不同或者从左向 右数花的编号序列不同。

为了避免输出过大，答案对一个参数 p 取模

【输入格式】

输入文件名为 ilove.in。

输入文件中有且仅有一组数据，只有一行四个数字，分别代表 type,n,m,p。其中 type 是一个帮助你判断测试点类型的参数，会在数据范围中说明。

【输出格式】

输出文件名为 ilove.out。

输出一行一个数字，代表答案对 p 取模的结果。

【输入输出样例 】

【数据规模与约定】

---

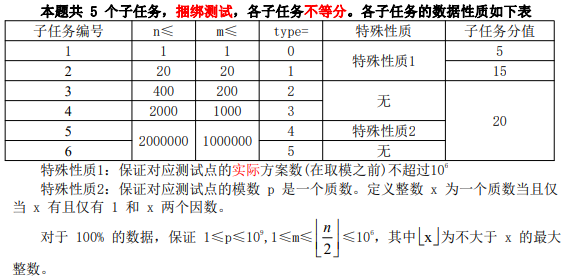
然后这套题的最后有句话：

（我恨了）

好了下面来说正解

---

SOLUTION：

首先，这是一道五三上的原题，所以它一定可以用数学的方法来计算。

其实这是一道zhx问题，但当你找不到思路时，不妨在考场上打打表找规律

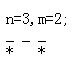
如果关心排列顺序的话，每个n与m的组合似乎都对应一个排列数呢qwq

n=8，m=3对应排列数：C₆³，n=7，m=3对应排列数：C₅³

而样例对应的C₂²，再仔细观察，不难推测对应的排列数与n和m的取值有关，于是我们大胆假设，在不考虑排列顺序的前提下，这m盆花摆在n个位置的方案数是C_n-m+1^m（好啦数学证明一下）

（对于任意两盆海棠花，不可以相邻的种植，那么每盆海棠花相当于占据了两个位置，因为会有一盆并不需要占据，例如对于三盆花，需要占据五个位置，所以我们用n-m+1，直接删去一定不能占的位置，或者我们可以感性的理解成：先将这m盆花放到n-m+1个位置中（不考虑空隙），如果两盆花相邻了，就加一个空位在这两盆花中间。那么方案数就是将m盆花摆放在n-m+1个空位中的方案数）

求出了所有组合方案后，对于每种方案，都有A_m^m种不同的排列方法，所以最后答案就是：

C_n-m+1^m*A_m^m

但是问题来了，看数据范围：

这可了不得了，这怎么算啊；

其实上面的式子可以展开再化简：

C_n-m+1^m=（n-m+1）！ /m！*（n-2m+1）！

A_m^m=m！；

C_n-m+1^m*A_m^m=（n-m+1）！/（n-2m+1）！

=（n-m+1）*（n-m）*……*（n-2m+2）；

所以这样就可以用很短的代码直接for循环出来啦：

#include<bits/stdc++.h>

using namespace std;

inline long long read(){
    long long ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch<=''&&ch>='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

long long type,n,m,p;

int main(){
    type=read();n=read();m=read();p=read();
    long long ans=;
    for(int i=n-*m+;i<=n-m+;i++)
      ans=(ans*i)%p;
    printf("%d",ans%p);
    return ;
}

毕竟zay写了题解，所以我们放一下：

end-