Andrew Ng机器学习公开课笔记 -- Logistic Regression

网易公开课，第3，4课
notes，http://cs229.stanford.edu/notes/cs229-notes1.pdf

前面讨论了线性回归问题，
符合高斯分布，使用最小二乘来作为损失函数

下面继续讨论分类问题，分类问题和回归问题不同在于Y的取值是离散的
我们先讨论最简单的binary classification，即Y的取值只有0和1
分类问题一般不会使用回归模型，因为回归模型是输出是连续的，而分类问题需要的输出是离散的

但是一定要用也不是不可以，比如这里继续使用线性回归模型，但是不是非常适合
原因如下，
首先线性模型的Y取值是连续，且没有限制的，而二元分类的取值为[0,1]，对于线性回归模型，参考下图，可以以0.5为分界线，大于则取1，小于则取0，也可以转化为离散的结果
再者，其实只有在分界线周围的样本点对分类模型会有比较大的影响，而比较远的样本点其实对模型没啥影响
但对于线性模型而言，增加任何样本点都会对模型产生相同的影响

所以提出logistic回归模型，这种回归模型可以比较好的解决二元分类问题
从本质上你仍然可以把他理解为线性模型，
你可以看下面给出的H函数，只是在线性回归外面加上logistic函数进行转换，可以理解成把上图的直线转化为那条sigmoid曲线，使其更加符合二元分类的需求
但是本质上可以看成仍然是用那条直线进行划分
参考，对线性回归，logistic回归和一般回归的认识

 

Logistic function（Sigmoid function）
下面给出H函数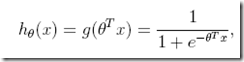

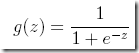
由这个函数生成的曲线称为Sigmoid曲线，这个曲线很有说道，参考http://t.cn/8st3jG1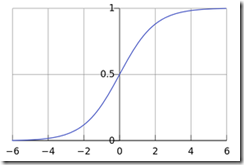

先不从数学上说为什么这个模型中二元分类上比线性模型好，单纯从图形上看就可以得到直观的结论
首先Y值域在[0,1]，其次图形中中间陡峭而两边平缓，符合二元分类的样本点特性

确定了模型，下面要做的是fit最优的θ，仍然是采用最大似然法，即找出对训练数据可能性最大的那个θ

前面对于线性回归问题，符合高斯分布（连续回归问题往往符合高斯分布），最终我们由最大似然推导出最小二乘回归
但是对于二元分类，符合伯努利分布（the Bernoulli distribution, 又称两点分布，0-1分布），因为二元分类的输出一定是0或1，典型的伯努利实验
by the way，二项分布是n次独立的伯努利实验形成的概率分布，当n=1时，就是伯努利分布
同样，如果离散输出是多个值，就是符合多项分布

看看由最大似然可以推导出什么
首先给出伯努利分布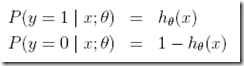

是否好理解，给定x;θ，y=1的概率等于h的值，看看图中，当然是h的值越大越可能为1，越小越可能为0
那么这个式子可以合并写成，比较tricky的写法，Y为0或1，总有一项为1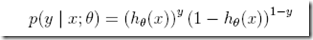

那么θ的似然函数定义为，θ的可能性取决于模型对训练集拟合的好坏
 
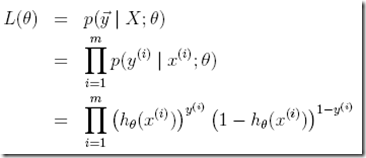
同样为了数学计算方便，定义log likelihood，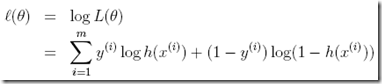

很显然，对于伯努利分布，这里无法推导出最小二乘呵呵
下面要做的是找到θ使得ℓ(θ)最大，由于这里是找最大值而非最小值，所以使用梯度上升（gradient ascent），道理是一样的
首先计算梯度，计算过程参考原文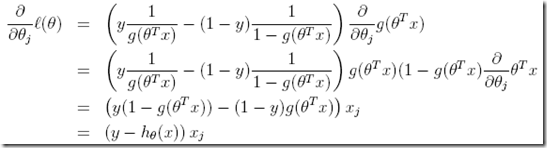

所以最终随机梯度上升rule写成，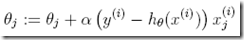

这个梯度公式，奇迹般的和线性回归中的梯度公式表面上看是一样的，可以仔细比较一样的
之所以说表面上，是因为其中的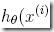 是不同的，这里是logitics函数

 

Perceptron Learning Algorithm（感知机算法）
这里谈感知机，好像有些离题，但是你看下感知机的函数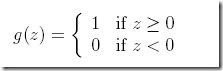
 
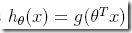
单纯从直观图形的角度，似乎是逻辑函数的简化形式
逻辑函数是连续的在[0,1]区间上，而感知机直接非0则1，参考下图红线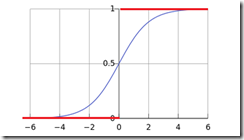
 
同样使用梯度下降的感知机算法也是和上面相同的形式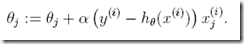

同样不同的仅仅是h(x)
1960s，感知机被看作是大脑工作中独立神经元的粗糙的模型，由于简单，会用作后面介绍的学习算法的起点
虽然直观看上去感知机和之前看到的logistic回归或最小二乘回归很像，但是其实是非常不一样的算法
因为，对于感知机，很难赋予一种有意义的概率解释（probabilistic interpretations），或使用最大似然估计算法来推导感知机算法
而对于最小二乘或logistic都可以给出像高斯分布或伯努利分布的概率解释，并可以使用最大似然进行推导

 

牛顿算法（Newton’s method）
前面我们说道使用梯度上升法来求解maximizing ℓ(θ)
现在介绍另外一种收敛速度更快的算法来求解，称为牛顿法
也很简单，看下面的图

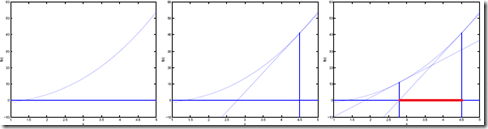
对于梯度下降，每次只是在梯度方向（导数，切线）下降一小步（取决于学习速度参数）
而牛顿法是一直下降到导数（切线）和θ轴交界的那个θ，直观上可以看出这个下降速度确实很快
而其中θ下降了图中红线部分，通过三角计算很容易算出
故牛顿法的rule为，最终找到f(θ) = 0的点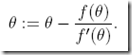

好，现在看我们的问题，解逻辑回归就是要找到max(ℓ )，即ℓ′(θ)=0的点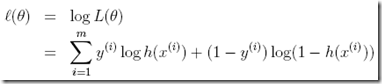

代入牛顿法，即f(θ) = ℓ′(θ)
所以逻辑回归的牛顿法的rule公式，写为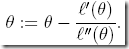

但这里我们只是考虑一个θ的情况，实际情况下参数会有多个，即θ其实是一个向量
那么对于θ向量，牛顿法的公式会变成怎样？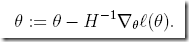

其中∇ℓ(θ)也是个向量，是ℓ(θ)对于每个θi的偏导的结果
其中H是个n-by-n matrix，其实一般是n + 1-by-n + 1，因为如果有n个参数θi，还会有个截距项
H矩阵称为Hessian，矩阵中每一项定义为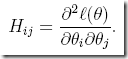
 

和梯度下降比，牛顿法会带来更快的收敛速度和更少的迭代次数
但相应的每次迭代会需要更大的计算量，因为需要计算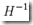
所以当θ的参数个数不是很多的时候，牛顿法会比较适合