什么是马拉车算法（Manacher's Algorithm）？

提出问题

最长回文子串问题：给定一个字符串，求它的最长回文子串长度。

如果一个字符串正着读和反着读是一样的，那它就是回文串。如a、aa、aba、abba等。

暴力解法

简单粗暴：找到字符串的所有子串，遍历每一个子串以验证它们是否为回文串。一个子串由子串的起点和终点确定，对于一个长度为n的字符串，共有n^2个子串。这些子串的平均长度大约是n/2，因此这个解法的时间复杂度是 \(O(n^3)\)。明显不可取。

方法改进

回文子串是连续的，而且是对称的。长度为奇数回文串以最中间字符的位置为对称轴左右对称，而长度为偶数的回文串的对称轴在中间两个字符之间的空隙。可否利用这种对称性来提高算法效率呢？答案是肯定的。我们知道整个字符串中的所有字符，以及字符间的空隙，都可能是某个回文子串的对称轴位置。可以遍历这些位置，在每个位置上同时向左和向右扩展，直到左右两边的字符不同，或者达到边界。对于一个长度为n的字符串，这样的位置一共有 n+n-1=2n-1 个，在每个位置上平均大约要进行 n/4 次字符比较，于是此算法的时间复杂度是 \(O(n^2)\)。

另外一种改进方法是利用动态规划，DP[i][j]定义成子串[i, j]是否是回文串。外循环 i从 n−1 往 0 遍历，内循环 j 从 i 往 n−1 遍历，若s[i]==s[j]：

• 若i==j，则dp[i][j]=true；
• 若i和j是相邻的，则dp[i][j]=true；
• 若i和j中间只有一个字符，则dp[i][j]=true；
• 否则，检查dp[i+1][j-1]是否为true，若为true，那么dp[i][j]就是true。

前三条可以合并，即 j−i≤2。求得dp[i][j]真值后，也可快速解决问题。时间复杂度：\(O(n^2)\)。

Manacher's Algorithm

对于 \(O(n^2)\) 的复杂度，或许还不满足，是否可以再优化一些呢？

先分析改进方法中的缺陷，利用回文中心需要分奇偶两种情况讨论，两种改进都会重复访问子串，降低效率。

Manacher's Algorithm正是针对这两个问题进行进一步的改进，将时间复杂度降到了神奇的 \(O(n)\)：

问题一：回文长度奇偶性问题

为了不区分奇偶两种情况，对字符串作预处理，在所有字符之间（包括首尾）插入相同字符如'#'，处理之后所有的子串都是奇数长度的。如aba→#a#b#a#。

插入的是同样的符号，且符号不存在于原串，因此子串的回文性不受影响，原来是回文的串，插完之后还是回文的，原来不是回文的，依然不会是回文。

问题二：重复访问问题

定义回文半径：回文串中最左或最右位置的字符与其对称轴的距离。算法中定义回文半径数组 \(RL\)，\(RL[i]\) 表示以第i个字符为对称轴的回文串的回文半径。

定义 \(MaxRight\)，表示当前访问到的所有回文子串，所能触及的最右一个字符的位置。另外还要记录下 \(MaxRight\) 对应的回文串的对称轴所在的位置，记为 \(pos\)。

核心代码：RL[i] = i < MaxRight ? min(RL[2*pos-i], MaxRight-i) : 1;

理解了这行代码，可以说就理解了这个算法。我们来分情况讨论：

（1）i < MaxRight时，可以再分两种情况：

①MaxRight - i > RL[2*pos-i]，如下图，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]。

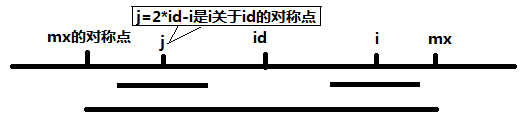
②MaxRight - i ＜ RL[2*pos-i]，如下图，以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。

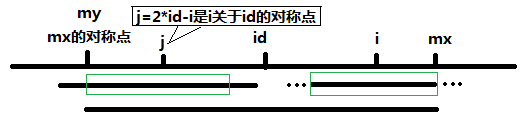
（2）i ＞ MaxRight时，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去慢慢匹配了。

代码实现

返回最长的回文子串。代码中resLen为处理后字符串的最大回文半径，对应到原来的字符串中时，只需-1即是整个回文串的长度。

string Manacher(string s) {
    //预处理
    string t = "#";
    for (int i = 0; i < s.size(); ++i) {
        t += s[i];
        t += "#";
    }

    vector<int> RL(t.size(), 0);
    int MaxRight = 0, pos = 0;
    int resLen = 0, resCenter = 0;
    for (int i = 0; i < t.size(); ++i) {
        RL[i] = MaxRight > i ? min(RL[2 * pos - i], MaxRight - i) : 1;

        while (i-RL[i] >=0 && i+RL[i] < t.size() && t[i + RL[i]] == t[i - RL[i]])//扩展，注意边界
            ++RL[i];
        //更新最右端及其中心
        if (MaxRight < i + RL[i] -1) {
            MaxRight = i + RL[i] -1;
            pos = i;
        }
        if (resLen < RL[i]) {
            resLen = RL[i];
            resCenter = i;
        }
    }
    return s.substr((resCenter - resLen + 1) / 2 , resLen - 1);
}

时间复杂度：\(O(n)\)。在参考链接中有比较详细的证明过程。

参考链接：https://segmentfault.com/a/1190000003914228

参考链接：http://www.cnblogs.com/grandyang/p/4475985.html