题解 洛谷 P2287 [USACO07NOV]Sunscreen G

原题

传送门

有C个奶牛去晒太阳 (1 <=C <= 2500)，每个奶牛各自能够忍受的阳光强度有一个最小值和一个最大值(minSPFi and maxSPFi)，太大就晒伤了，太小奶牛没感觉。
而刚开始的阳光的强度非常大，奶牛都承受不住，然后奶牛就得涂抹防晒霜，防晒霜的作用是让阳光照在身上的阳光强度固定为某个值。
那么为了不让奶牛烫伤，又不会没有效果。
给出了L种防晒霜。每种的数量和固定的阳光强度(coveri and SPFi)也给出来了
每个奶牛只能抹一瓶防晒霜，最后问能够享受晒太阳的奶牛有几个。

思路

声明

minSPFi : 奶牛忍受的阳光强度最小值
maxSPFi : 奶牛忍受的阳光强度最大值
coveri : 防晒霜数量
SPFi ： 防晒霜阳光强度

初始的思路(38 pts)

这是一道贪心题,但我开始时还是想错了。

我先将每头牛按照最小忍受阳光强度从小到大排序，防晒霜按照强度从小到大排序。

然后开始枚举，对于第 \(i\) 个奶牛 ，假设当前枚举到第 \(l\) 个 防晒霜 , 当其 \(SPFi < minSPFi\) , \(l++\) ,直到满足 \(SPFi \ge minSPFi\) ，而当 \(SPFi > maxSPFi\) , 则 continue ,最后判断一下防晒霜剩余个数即可判断答案

初始代码（38 pts)

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int MAXN = 2510;
int C,L,ans,l = 0;

struct cow{//奶牛
	int l,r;
	bool operator < (const cow &b) const{
		if(l == b.l) return r < b.r;
		return l < b.l;
	}
}a[MAXN];

struct sunscreen{//防晒霜
	int SP,num;
	bool operator < (const sunscreen &b) const{
		return SP < b.SP;
	}
}lotion[MAXN];

int main (){
	scanf("%d %d",&C,&L);
	for(int i = 0 ;i < C;i++) scanf("%d %d",&a[i].l,&a[i].r);
	for(int i = 0 ;i < L;i++) scanf("%d %d",&lotion[i].SP,&lotion[i].num);
	sort( a , a+C );
	sort( lotion , lotion+L);
	for(int i = 0 ;i < C;i++){
		if(lotion[l].num == 0) l++; //判断个数
		while ( a[i].l > lotion[l].SP && l < L-1) l++;//查找左端点是否符合条件
		if( a[i].r < lotion[l].SP) continue;//右端点不符合直接跳过
		lotion[l].num--;
		ans++;//答案处理
	}
	printf("%d",ans);
	return 0;
}

正解思路

然鹅，这种贪心错了。

举个例子：



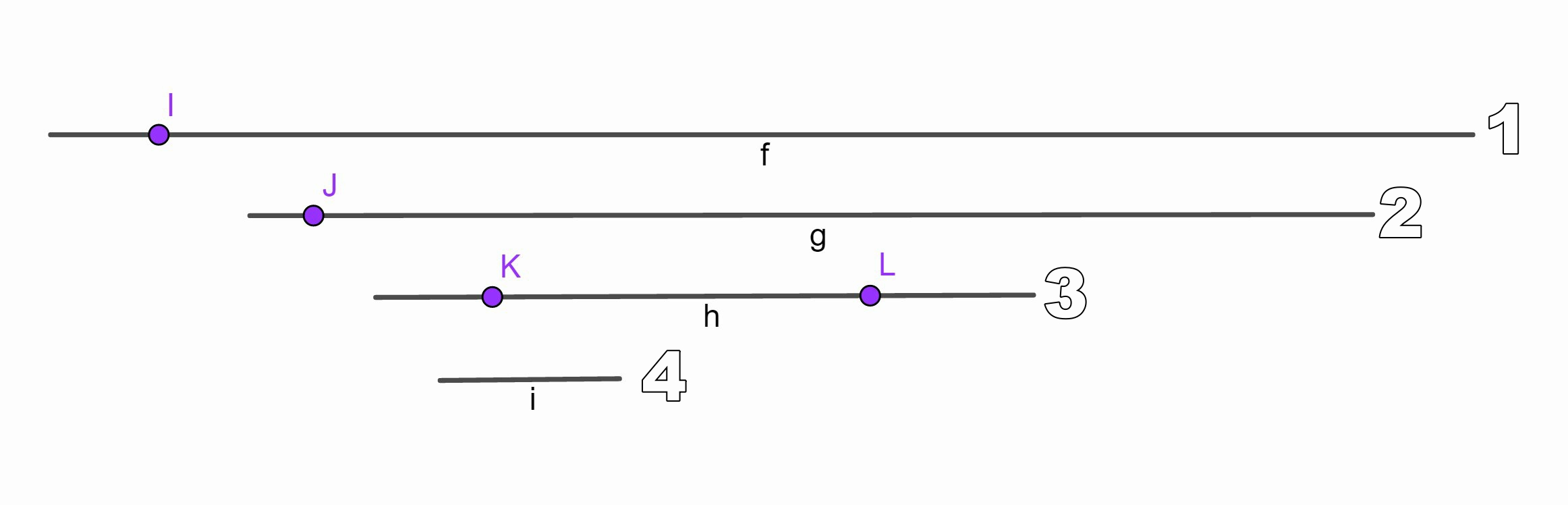
按照这种算法，我们会让 1 区间使用 I ，2区间使用 J，3 区间使用 K ，答案为 3。

但是答案为4。

正确解法应该为：

先将每头牛按照最小忍受阳光强度从大到小排序，然后开始枚举，对于第 \(i\) 个奶牛 ，我们要找到它能用的防晒霜里面SPFi最大的，然后计算答案。

关于正确性

SPFi更小的显然其他没枚举到的牛很可能会被用到，于是我们拿掉SPFi最大的，具体可以见上面的图。

代码

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int MAXN = 2510;
int C,L,ans;

struct cow{
	int l,r;
	bool operator < (const cow &b) const{
		return l > b.l;
	}
}a[MAXN];

struct sunscreen{
	int SP,num;
}lotion[MAXN];

int main (){
	scanf("%d %d",&C,&L);
	for(int i = 0 ;i < C;i++) scanf("%d %d",&a[i].l,&a[i].r);
	for(int i = 0 ;i < L;i++) scanf("%d %d",&lotion[i].SP,&lotion[i].num);
	sort( a , a+C );
	for(int i = 0 ;i < C;i++){
		int l = -1,choose = -1;
		for(int j = 0;j < L;j++)//暴力枚举
			if ( lotion[j].num > 0 && lotion[j].SP >= a[i].l && lotion[j].SP <= a[i].r)
				if(lotion[j].SP > choose){
					choose = lotion[j].SP;
					l = j;
				}
		if( l != -1 ){
			ans++;
			lotion[l].num--;
		}//答案处理
	}
	printf("%d",ans);
	return 0;
}