Johnson全源最短路

例题：P5905 【模板】Johnson 全源最短路

首先考虑求全源最短路的几种方法：

• Floyd：时间复杂度\(O(n^3)\)，可以处理负权边，但不能处理负环，而且速度很慢。
• Bellman-Ford：以每个点为源点做一次Bellman-Ford，时间复杂度\(O(n^2m)\)，可以处理负权边，可以处理负环，但好像比Floyd还慢？
• dijkstra：以每个点为源点做一次dijkstra，时间复杂度\(O(nmlogm)\)，不能处理负权边，但比前面两个快多了。

好像……只有dijkstra还有希望？但负权边处理不了真是很棘手啊。

一种方法是让每条边都加上一个数\(x\)使得边权为正，但考虑下图：



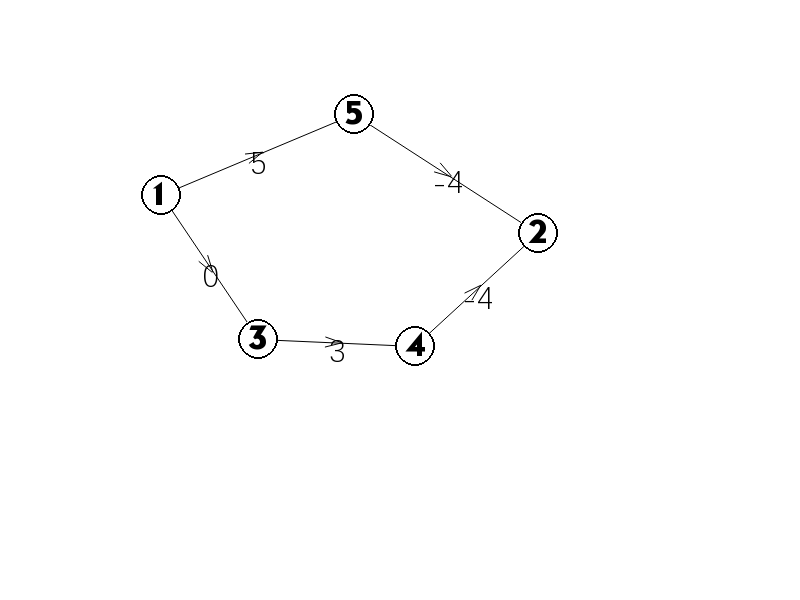
\(1\)到\(2\)的最短路应为：\(1 -> 3 -> 4 -> 2\)，长度为\(-1\)。如果我们把每条边的边权都加上\(5\)：



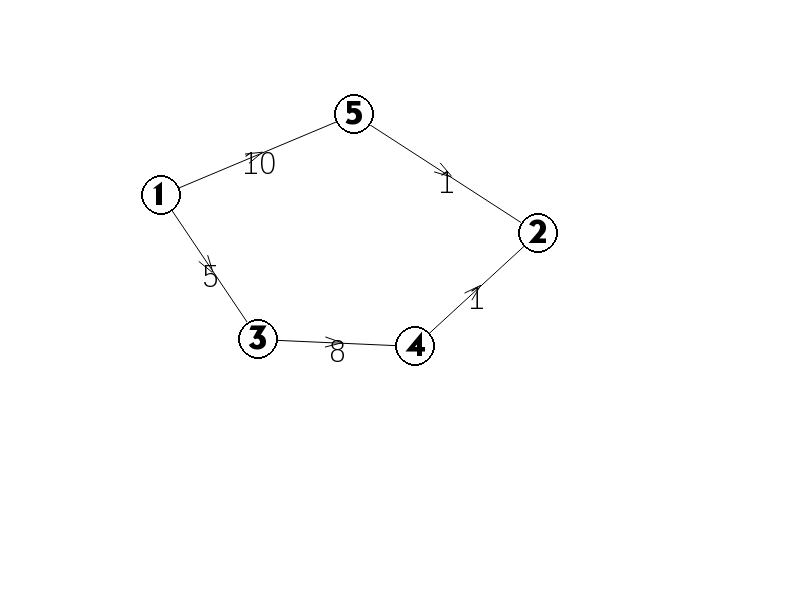
此时的最短路是：\(1 -> 5 -> 2\)，就不是实际的最短路了，所以这种方法行不通

注：经本人研究，应该是两条路径进过的边的数量不同而导致的

接下来，就该 Johnson 登场啦！Johnson 其实就是用另一种方法标记边权啦。

首先来看看实现方法：我们新建一个虚拟结点（不妨设他的编号为0），由他向其他的所有结点都连一条边权为\(0\)的边，然后求0号节点为源点的单源最短路，存到一个\(h\)数组中。然后，让每条边的权值\(w\)变为\(w+h_u-h_v\)，这里\(u\)和\(v\)分别为这条边的起点和终点。然后再以每个点为源点做 dijkstra 就OK了。

Q：那这么说，Dijkstra 也可以求出负权图（无负环）的单源最短路径了？

A：没错。但是预处理要跑一遍 Bellman-Ford，还不如直接用 Bellman-Ford 呢。

如何证明这是正确的呢？

首先，从\(s\)到\(t\)的路径中随便取出一条：

\[s -> p_1 -> p_2 -> \cdots -> p_k -> t
\]

则这条路径的长度为：

\[(w_{s,p_1}+h_s-h_{p_1})+(w_{p_1,p_2}+h_{p_1}-h_{p_2})+\dots+(w_{p_k,t}+h_{p_k}-h_t)
\]

简化后得到：

\[w_{s,p_1}+w_{p_1,p_2}+\cdots+w_{p_k,t}+h_s-h_t
\]

可以发现，不管走哪条路径，最后都是\(+h_s-h_t\)，而\(h_s\)和\(h_t\)又是不变的，所以最终得到的最短路径还是原来的最短路径。

到这里已经证明一半了，接下来要证明得到的边权非负，必须要无负权边才能使 dijkstra 跑出来的结果正确。根据三角形不等式（就是那个三角形里任意两条边的长度之和大于等于另一条边的长度），新图上的任意一条边\((u,v)\)上的两点满足：\(h_v \le w_{u,v}+h_u\)，则新边的边权\(w_{u,v}+h_u-h_v \ge 0\)。所以新图的边权非负。

正确性证明就是这个亚子。

代码实现（注意处理精度问题，该开ll的时候开ll）：

#include<cstdio>
#include<queue>
#define MAXN 5005
#define MAXM 10005
#define INF 1e9
using namespace std;
int n,m;
int vis[MAXN];
long long h[MAXN],dis[MAXN];
bool f[MAXN];
struct graph
{
	int tot;
	int hd[MAXN];
	int nxt[MAXM],to[MAXM],dt[MAXM];
	void add(int x,int y,int w)
	{
		tot++;
		nxt[tot]=hd[x];
		hd[x]=tot;
		to[tot]=y;
		dt[tot]=w;
		return ;
	}
}g;//链式前向星
bool SPFA(int s)//这里用了Bellman-Ford的队列优化
{
	queue<int>q;
	for(int i=1;i<=n;++i) h[i]=INF,f[i]=false;
	h[s]=0;
	f[s]=true;
	q.push(s);
	while(!q.empty())
	{
		int xx=q.front();
		q.pop();
		f[xx]=false;
		for(int i=g.hd[xx];i;i=g.nxt[i])
			if(h[g.to[i]]>h[xx]+g.dt[i])
			{
				h[g.to[i]]=h[xx]+g.dt[i];
				if(!f[g.to[i]])
				{
					if(++vis[g.to[i]]>=n) return false;//注意在有重边的情况下要记录入队次数而不是松弛次数
					f[g.to[i]]=true,q.push(g.to[i]);
				}
			}
	}
	return true;
}
void dijkstra(int s)
{
	priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
	for(int i=1;i<=n;i++) dis[i]=INF,f[i]=false;
	q.push(make_pair(0,s));
	dis[s]=0;
	while(!q.empty())
	{
		int xx=q.top().second;
		q.pop();
		if(!f[xx])
		{
			f[xx]=true;
			for(int i=g.hd[xx];i;i=g.nxt[i])
				if(dis[g.to[i]]>dis[xx]+g.dt[i])
				{
					dis[g.to[i]]=dis[xx]+g.dt[i];
					if(!f[g.to[i]])
						q.push(make_pair(dis[g.to[i]],g.to[i]));
				}
		}
	}
	return ;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		g.add(u,v,w);
	}
	for(int i=1;i<=n;i++) g.add(0,i,0);//建虚拟节点0并且往其他的点都连一条边权为0的边
	if(!SPFA(0))//求h的同时也判了负环
	{
		printf("-1");
		return 0;
	}
	for(int u=1;u<=n;u++)
		for(int i=g.hd[u];i;i=g.nxt[i])
			g.dt[i]+=h[u]-h[g.to[i]];//求新边的边权
	for(int i=1;i<=n;i++)
	{
		dijkstra(i);//以每个点为源点做一遍dijkstra
		long long ans=0;
		for(int j=1;j<=n;j++)//记录答案
			if(dis[j]==INF) ans+=1ll*j*INF;
			else ans+=1ll*j*(dis[j]+(h[j]-h[i]));
		printf("%lld\n",ans);
	}
	return 0;
}

最后安利一发博客