C++ 数据结构 2：栈和队列

1 栈

1.1 栈的基本概念

栈（stack）又名堆栈，它是一种 运算受限的线性表。限定 仅在表尾进行插入和删除操作 的线性表。表尾被称为栈顶，相对地，把另一端称为栈底。

1.1.1 特点

它的特殊之处在于限制了这个线性表的插入和删除的位置，它始终只在栈顶进行。这也就使得：栈底是固定的，最先进栈的只能在栈底。

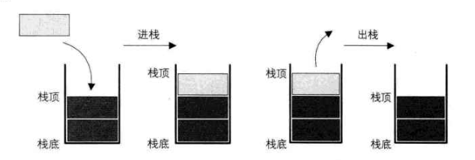
1.2 栈的常用操作

• 创建栈

• 销毁栈

• 清空栈

• 进栈

• 出栈

• 获取栈顶元素

• 获取栈的大小

1.2.1 栈的抽象数据类型

ADT 栈（stack）
Data
	通线性表。元素具有相同的类型，相邻的元素具有前驱和后继关系。
Operation
	// 初始化，建立一个空栈S
	InitStack(*S);
	// 若栈存在，则销毁它
	DestroyStack(*S);
	// 将栈清空
	ClearStack(*S);
	// 若栈为空则返回true，否则返回false
	StackEmpty(S);
	// 若栈存在且非空，用e返回S的栈顶元素
	GetTop(S，*e);
	// 若栈S存在，插入新元素e到栈S中并成为其栈顶元素
	Push(*S，e);
	// 删除栈S中的栈顶元素，并用e返回其值
	Pop（*S, *e）;
	// 返回栈S的元素个数
	StackLength(S);
endADT

1.3 栈的顺序存储

1.3.1 基本概念

基本概念：

栈的顺序存储结构简称顺序栈，它是运算受限制的顺序表。顺序栈的存储结构是：利用一组地址连续的的存储单元依次存放自栈底到栈顶的数据元素，同时附设指针top只是栈顶元素在顺序表中的位置。

栈是先进后出的线性表。

1.3.2 设计与实现

因为栈是一种特殊的线性表，所以栈的顺序存储可以通过顺序线性表来实现。

示例代码：

SqStack.h

#ifndef _SQSTACK_H
#define _SQSTACK_H
#define MAXSIZE 50
typedef int EnumType;
typedef struct _SQSTACK
{
	int top;	// 栈顶指针
	EnumType data[MAXSIZE];
}SqStack;
// 初始化，建立一个空栈S
void InitStack(SqStack *S);
// 将栈清空
void ClearStack(SqStack *S);
// 若栈为空则返回true，否则返回false
int StackEmpty(SqStack S);
// 若栈存在且非空，用e返回S的栈顶元素
void GetTop(SqStack S, EnumType *e);
// 若栈S存在，插入新元素e到栈S中并成为其栈顶元素
void Push(SqStack *S, EnumType e);
// 删除栈S中的栈顶元素，并用e返回其值
void Pop(SqStack *S, EnumType *e);
// 返回栈S的元素个数
int StackLength(SqStack S);
#endif // _SQSTACK_H

SqStack.c

#include "SqStack.h"
#include <string.h>
void InitStack(SqStack *S)
{
	// 空栈
	S->top = -1;
	memset(S->data, 0, sizeof(S->data));
}
void ClearStack(SqStack *S)
{
	S->top = -1;
}
int StackEmpty(SqStack S)
{
	if (S.top == -1)
	{
		return 1;
	}
	return 0;
}
void GetTop(SqStack S, EnumType *e)
{
	// 栈为空
	if (S.top == -1 && S.data[S.top]!= 0)
	{
		return;
	}
	*e = S.data[S.top];
}
void Push(SqStack *S, EnumType e)
{
	// 栈已经满了
	if (S->top == MAXSIZE - 1)
	{
		return;
	}
	// 栈顶上移
	S->top++;
	// 赋值
	S->data[S->top] = e;
}
void Pop(SqStack *S, EnumType *e)
{
	// 栈为空
	if (S->top == -1 && S->data[S->top]!= 0)
	{
		return;
	}
	// 赋值
	*e = S->data[S->top];
	// 栈顶指针下移
	S->top--;
}
int StackLength(SqStack S)
{
	return S.top + 1;
}

main.c

#include "SqStack.h"
#include <stdio.h>
#include <stdlib.h>
void main()
{
	// 定义栈变量
	SqStack st;
	int i = -1;
	// 初始化栈
	InitStack(&st);
	// 压栈
	for (i = 0; i < 10; ++i)
	{
		Push(&st,i+1);
	}
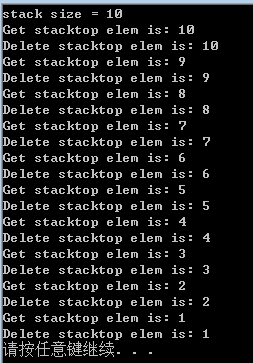
	printf("stack size = %d\n", StackLength(st));
	// 出栈
	while (StackEmpty(st) != 1)
	{
		int temp;
		// 取栈顶元素
		GetTop(st, &temp);
		printf("Get stacktop elem is: %d\n", temp);
		// 删除栈顶元素
		Pop(&st, &temp);
		printf("Delete stacktop elem is: %d\n", temp);
	}
	system("pause");
}

运行结果：

1.4 栈的链序存储

1.4.1 基本概念

栈的链式存储结构简称链栈。

1.4.2 设计与实现

链栈是一种特殊的线性表，链栈可以通过链式线性表来实现。

示例代码：

LinkStack.h

#ifndef _LINKSTACK_H
#define _LINKSTACK_H
// 定义小链表节点
typedef struct NODE
{
	struct NODE* next;
}Node;
// 链表结构体
typedef struct
{
	// 栈顶指针
	Node *top;
	// 长度
	int length;
}LinkStack;
// 初始化，建立一个空栈S
void InitStack(LinkStack *S);
// 将栈清空
void ClearStack(LinkStack *S);
// 若栈为空则返回true，否则返回false
int StackEmpty(LinkStack S);
// 若栈存在且非空，用e返回S的栈顶元素
void GetTop(LinkStack S, Node **e);
// 若栈S存在，插入新元素e到栈S中并成为其栈顶元素
void Push(LinkStack *S, Node *e);
// 删除栈S中的栈顶元素，并用e返回其值
void Pop(LinkStack *S, Node **e);
// 返回栈S的元素个数
int StackLength(LinkStack S);
#endif	// _LINKSTACK_H

LinkStack.c

#include "LinkStack.h"
#include <stdio.h>
void InitStack(LinkStack *S)
{
	S->length = 0;
	S->top = NULL;
}
void ClearStack(LinkStack *S)
{
	while (S->length)
	{
		Node* p;
		Pop(S, &p);
	}
}
int StackEmpty(LinkStack S)
{
	if (S.length == 0)
	{
		return 1;
	}
	return 0;
}
void GetTop(LinkStack S, Node **e)
{
	// 空栈
	if (S.length == 0 || S.top == NULL)
	{
		return;
	}
	*e = S.top;
}
// 栈顶是链表头部
void Push(LinkStack *S, Node *e)
{
	// 节点e插入到链表的头部
	e->next = S->top;
	// top指针指向第一个节点
	S->top = e;
	// 长度+1
	S->length++;
}
void Pop(LinkStack *S, Node **e)
{
	// 删除第一个节点
	Node* pDel = S->top;
	// 空栈
	if (S->length == 0)
	{
		return;
	}
	// 赋值
	*e = pDel;
	// 栈顶指针后移
	S->top = pDel->next;
	// 长度减1
	S->length--;
}
int StackLength(LinkStack S)
{
	return S.length;
}

main.c

#include <stdio.h>
#include <stdlib.h>
#include "LinkStack.h"
// 业务节点
typedef struct stu
{
	// 包含链表节点
	Node node;
	int id;
	int age;
}Student;
void main()
{
	Student stu[10];
	// 链表结构变量
	LinkStack st;
	int i = -1;
	// 初始化栈
	InitStack(&st);
	// 初始化数组
	for (i = 0; i < sizeof(stu) / sizeof(Student); ++i)
	{
		stu[i].id = i;
		stu[i].age = i + 20;
		// 数据添加链表中
		Push(&st, &stu[i].node);
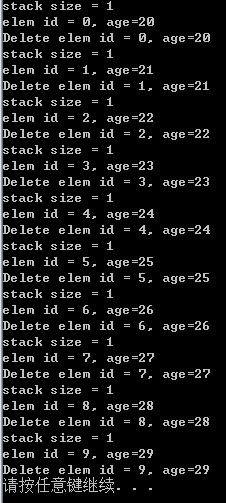
		printf("stack size = %d\n", StackLength(st));
		while (StackEmpty(st) != 1)
		{
			Node* p = NULL;
			Student* pp = NULL;
			// 获取栈顶元素
			GetTop(st, &p);
			pp = (Student*)p;
			printf("elem id = %d, age=%d\n", pp->id, pp->age);
			// 删除
			Pop(&st, &p);
			pp = (Student*)p;
			printf("Delete elem id = %d, age=%d\n", pp->id, pp->age);
		}
	}
	system("pause");
}

运行结果：

2 队列

2.1 基本概念

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

2.1.1 特点

队列是先进先出的线性表。

在队尾添加元素，在队头删除元素。

判断队列是空队列还是已满呢？

1. 栈空： 队首标志 = 队尾标志时，表示栈空。

2. 栈满 : 队尾 + 1 = 队首时，表示栈满。

2.2 队列的常用操作

• 创建队列

• 销毁队列

• 清空队列

• 进队列

• 出队列

• 获取队头元素

• 获取队列的长度

2.2.1 队列的抽象数据类型

ADT 队列（Queue）
Data
	通线性表。元素具有相同的类型，相邻元素具有前驱后继关系。
Operation
	// 初始化操作，建立一个空队列Q
	InitQueue（*Q）；
	// 若队列Q存储，则销毁它。
	DestroyQueue(*Q);
	// 将队列Q清空
	ClearQueue(*Q);
	// 若队列为空则返回true，否则返回false
	QueueEmpty(Q);
	// 若队列Q存在且非空，用e返回队列Q的队头元素
	GetHead(Q, *e);
	// 若队列Q存在，插入新元素e到队列Q中并成为队尾元素。
	EnQueue(*Q, e);
	// 删除队列Q中的队头元素，并用e返回其值
	DeQueue(*Q, *e);
	// 返回队列Q的元素个数
	QueueLength(Q);
endADT

2.3 队列顺序模型和链表模型关系分析

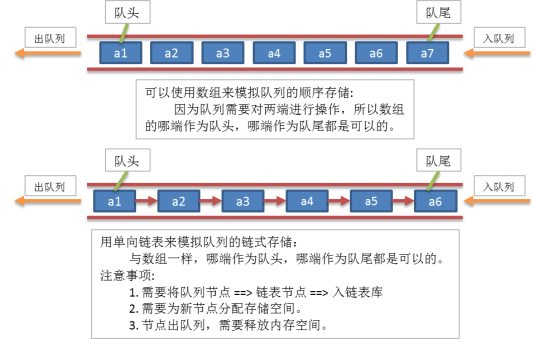
2.4 队列的顺序存储

2.4.1 基本概念

队列也是一种特殊的线性表；可以用线性表顺序存储来模拟队列。

2.4.2 设计与实现

示例代码：

SqQueue.h

#ifndef _SQQUEUE_H
#define _SQQUEUE_H
#define MAXSIZE 50
typedef int EnumType;
typedef struct _SQQUEUE
{
	// 尾节点指针
	int rear;
	// 头结点指针
	int front;
	EnumType data[MAXSIZE];
}SqQueue;
// 初始化操作，建立一个空队列Q
void InitQueue(SqQueue *Q);
// 将队列Q清空
void ClearQueue(SqQueue *Q);
// 若队列为空则返回true，否则返回false
int QueueEmpty(SqQueue Q);
// 若队列Q存在且非空，用e返回队列Q的队头元素
void GetHead(SqQueue Q, EnumType* e);
// 若队列Q存在，插入新元素e到队列Q中并成为队尾元素。
void EnQueue(SqQueue *Q, EnumType e);
// 删除队列Q中的队头元素，并用e返回其值
void DeQueue(SqQueue *Q, EnumType* e);
// 返回队列Q的元素个数
int QueueLength(SqQueue Q);
#endif	//_SQQUEUE_H

SqQueue.c

#include "SqQueue.h"
#include <string.h>
void InitQueue(SqQueue *Q)
{
	Q->rear = Q->front = 0;
	memset(Q->data, 0, sizeof(Q->data));
}
void ClearQueue(SqQueue *Q)
{
	Q->rear =  Q->front = 0;
	memset(Q->data, 0, sizeof(Q->data));
}
int QueueEmpty(SqQueue Q)
{
	if (Q.rear == Q.front)
	{
		return 1;
	}
	return 0;
}
// 返回队首元素的值，但不删除该元素
void GetHead(SqQueue Q, EnumType* e)
{
	// 队列为空
	if (Q.rear == Q.front)
	{
		return;
	}
	*e = Q.data[Q.front];
}
// 在队尾压入新元素
void EnQueue(SqQueue *Q, EnumType e)
{
	// 队列已经满了
	if (Q->rear -1 == MAXSIZE)
	{
		return;
	}
	else
	{
		// 赋值
		Q->data[Q->rear] = e;
		// 队尾上移
		Q->rear++;
	}
}
// 删除队列首元素
void DeQueue(SqQueue *Q, EnumType* e)
{
	// 队列为空
	if (Q->rear == Q->front)
	{
		return;
	}
	// 赋值
	*e = Q->data[Q->front];
	// front指针上移
	Q->front++;
}
int QueueLength(SqQueue Q)
{
	return Q.rear;
}

main.c

#include "SqQueue.h"
#include <stdio.h>
#include <stdlib.h>
void main()
{
	// 队列变量
	SqQueue q;
	int i = -1;
	// 初始化队列
	InitQueue(&q);
	// 入队列
	for (i = 0; i < 5; ++i)
	{
		EnQueue(&q, i+1);
	}
	printf("Queue size = %d\n", QueueLength(q));
	// 删除全部节点
	while (QueueEmpty(q) != 1)
	{
		int temp;
		// 取栈顶元素
		GetHead(q, &temp);
		printf("Queue head value = %d\n",temp);
		// 删除栈顶元素
		DeQueue(&q, &temp);
		printf("Delete stacktop elem is: %d\n", temp);
	}
	system("pause");
}

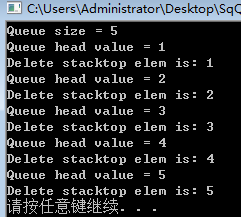
运行结果：

2.5 队列的链序存储设计与实现

2.5.1 基本概念

队列也是一种特殊的线性表；可以用线性表链式存储来模拟队列的链式存储。

2.5.2 设计与实现

示例代码：

LinkQueue.h

#ifndef _LINKQUEUE_H
#define _LINKQUEUE_H
typedef struct _NODE
{
	struct _NODE* next;
}Node;
typedef struct
{
	// 长度
	int length;
	// 尾节点指针
	Node *rear;
	// 头结点指针
	Node *front;
}LinkQueue;
// 初始化操作，建立一个空队列Q
void InitQueue(LinkQueue *Q);
// 将队列Q清空
void ClearQueue(LinkQueue *Q);
// 若队列为空则返回true，否则返回false
int QueueEmpty(LinkQueue Q);
// 若队列Q存在且非空，用e返回队列Q的队头元素
void GetHead(LinkQueue Q, Node** e);
// 若队列Q存在，插入新元素e到队列Q中并成为队尾元素。
void EnQueue(LinkQueue *Q, Node* e);
// 删除队列Q中的队头元素，并用e返回其值
void DeQueue(LinkQueue *Q, Node** e);
// 返回队列Q的元素个数
int QueueLength(LinkQueue Q);
#endif	//_LINKQUEUE_H

LinkQueue.c

#include "LinkQueue.h"
#include <stdio.h>
void InitQueue(LinkQueue *Q)
{
	Q->length = 0;
	Q->rear = NULL;
	Q->front = NULL;
}
void ClearQueue(LinkQueue *Q)
{
	while (Q->length)
	{
		Node* p;
		DeQueue(Q, &p);
	}
}
int QueueEmpty(LinkQueue Q)
{
	if (Q.length == 0)
	{
		return 1;
	}
	return 0;
}
// 链表的头部为队头, 尾部为队尾
void GetHead(LinkQueue Q, Node** e)
{
	// 错误处理
	if (Q.length == 0)
	{
		return;
	}
	*e = Q.front;
}
void EnQueue(LinkQueue *Q, Node* e)
{
	if (Q->length == 0)
	{
		// 空链表
		Q->rear = Q->front = e;
	}
	else
	{
		// 新节点放到队尾
		Q->rear->next = e;
		// rear指向最后一个节点
		Q->rear = e;
	}
	// 长度
	Q->length++;
}
void DeQueue(LinkQueue *Q, Node** e)
{
	if (Q->length == 0)
	{
		// 空链表
		return;
	}
	// 赋值
	*e = Q->front;
	// front指针后移
	Q->front = Q->front->next;
	// 长度
	Q->length--;
	if (Q->length == 0)
	{
		// 删除最后一个节点的时候, 尾指针需要指向NULL
		Q->rear = NULL;
	}
}
int QueueLength(LinkQueue Q)
{
	return Q.length;
}

main.c

#include "LinkQueue.h"
#include <stdio.h>
#include <stdlib.h>
void main()
{
	// 业务节点
	typedef struct _tag_value
	{
		// 包含一个链表节点
		Node node;
		// 数据
		int v;
	}Value;
	Value val[5];
	// 队列变量
	LinkQueue q;
	int i = -1;
	// init
	InitQueue(&q);
	for (i = 0; i < 5; ++i)
	{
		val[i].v = i + 20;
		// 入队列
		EnQueue(&q, &val[i].node);
	}
	printf("Queue size = %d\n", QueueLength(q));
	// 删除全部节点
	while (QueueEmpty(q) != 1)
	{
		// 取出队头元素
		Node* p;
		Value* pp;
		GetHead(q, &p);
		pp = (Value*)p;
		printf("Queue head value = %d\n", pp->v);
		// 出队列
		DeQueue(&q, &p);
		pp = (Value*)p;
		printf("Delete Queue head value = %d\n", pp->v);
	}
	system("pause");
}

运行结果：