六、Python集合定义和基本操作方法

一、集合的定义方法及特点

1、特点：

　　（1）由不同元素组成

#集合由不同元素构成
s={1,2,3,3,4,3,3,}
print(s)#运行结果：{1, 2, 3, 4}

　　（2）集合无序

#集合无序
s={'lilei','liuhua','alax','bob','bbb','bob'}
print(s)#运行结果：{'bob', 'liuhua', 'bbb', 'alax', 'lilei'}

　　（3）集合只能存放数字、字符串和元祖（即不可变类型）

#集合只能存放不可变类型
s={'alax',12,[1,2],('bab')}#[1,2]为列表类型
print(s)

　　运行结果：

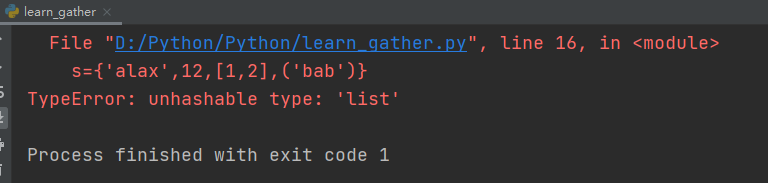
2、定义方式

　　类型一：s={ }

　　类型二：s=set( )

s=set('hel')
print(s)#输出结果：{'h', 'l', 'e'}

二、集合的内置方法

1、.add( )     添加（不可添加相同元素）

#添加
s1={1,2,3}
s1.add('alax')
print(s1)#输出结果：{1, 2, 3, 'alax'}
s2={1,2,3}
s2.add(3)
print(s2)#输出结果：{1, 2, 3}

2、.clear( )    清空、.copy( )   拷贝

#清空、拷贝
s={1,2,3}
s1={'baba'}
s.clear()
print(s)#输出结果：set()
s1.copy()
print(s1)#输出结果：{'baba'}

3、删除 .pop( ) 随机删除   .remove( )指定删除——>元素不存在会报错   .discard( )指定删除——>元素不存在不会报错

#删除
s1={'ax',1,2,3}
s1.pop()
print(s1)#运行结果：{1, 'ax', 2}
s2={'ax',1,2,3}
s2.remove('ax')
print(s2)#运行结果：{1, 2, 3}
#s2.remove('axxx')
#print(s2)#不存在，运行结果报错
s3={'ax',1,2,3}
s3.discard('axxxx')
print(s3)#运行结果：{1, 2, 3, 'ax'}，不存在但是不报错

二、集合关系运算、交叉，并集

1、基本关系运算

　　现在我们举一个例子

　　例：现在有同学'bob','alax','zh'学习Python，有同学'bob','zh'学习Linux，用列表统计处即学习Python也学习Linux的同学名单。

　　解答：此题使用列表解决有三种写法，如下所示:

#列表举例
python_l=['bob','alax','zh']
linux_l=['zh','bob']

# #方法一：
# for i in python_l:
#     for j in linux_l:
#         if i==j:
#             print(i)#运行结果：['bob', 'zh']

# #方法二：
# for name_l in python_l:
#     if name_l in linux_l:
#         print(name_l)#运行结果：['bob', 'zh']

#方法三：
python_l_and_linux_l=[]
for name_l in python_l:
    if name_l in linux_l:
        python_l_and_linux_l.append(name_l)
print(python_l_and_linux_l)#运行结果：['bob', 'zh']

　　现在我们用集合来解决此类问题：

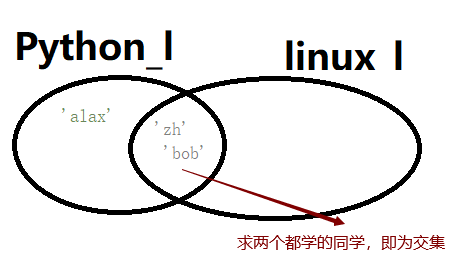
如上图所示，求即学习Python_l和Linux_l的同学，即求交集部分

（1）交集，A.intersection(B) A与B的交集  或者 A&B

　　例题所示代码表示为：

python_l=['bob','alax','zh']
linux_l=['zh','bob']
#——————转化为集合形式——————————
p_l=set(python_l)
l_l=set(linux_l)
#——————求两个集合的交集————————
print(p_l.intersection(l_l))#运行结果:{'zh', 'bob'}
print(p_l&l_l)#运行结果:{'zh', 'bob'}

　　补充：交集更新  A.intersection_updata(B)

（2）并集，A.union(B)  A与B的并集 或者A|B

#集合求并集
python_l=['bob','alax','zh']
linux_l=['zh','bob','hahah']
#——————转化为集合形式——————————
p_l=set(python_l)
l_l=set(linux_l)
#——————求两个集合的并集————————
print(p_l.union(l_l))#运行结果：{'alax', 'hahah', 'zh', 'bob'}
print(p_l|l_l)#运行结果：{'alax', 'hahah', 'zh', 'bob'}

（3）差集：即A中存在但是B中不存在的元素 　A.diference(B)   或者  A-B或者B-A

#集合求差集
python_l=['bob','alax','zh']
linux_l=['zh','bob','hahah']
#——————转化为集合形式——————————
p_l=set(python_l)
l_l=set(linux_l)
#——————求两个集合的差集————————
print(p_l-l_l)#运行结果：{'alax'}
print(l_l-p_l)#运行结果：{'hahah'}
print(p_l.difference(l_l))#运行结果：{'alax'}

　　图解如下：

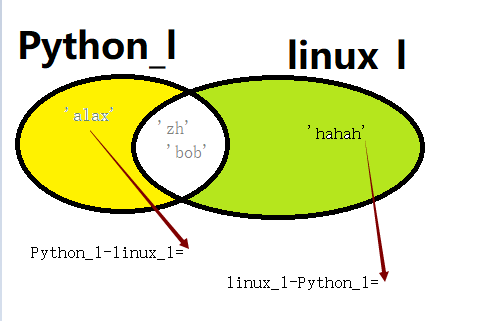
　　补充：差集更新

python_l=['bob','alax','zh','hghg']
linux_l=['zh','bob','hahah','hghg','hhhh']
#——————转化为集合形式——————————
p_l=set(python_l)
l_l=set(linux_l)
p_l.difference_update(l_l)
print(p_l)#运行结果：{'alax'}

（4）交叉补集   A.symmetric_difference(B)  或者  A^B

#交叉补集
python_l=['bob','alax','zh']
linux_l=['zh','bob','hahah']
#——————转化为集合形式——————————
p_l=set(python_l)
l_l=set(linux_l)
print(p_l.symmetric_difference(l_l))#运行结果：{'alax', 'hahah'}
print(p_l^l_l)#运行结果：{'alax', 'hahah'}

　　图解如下：

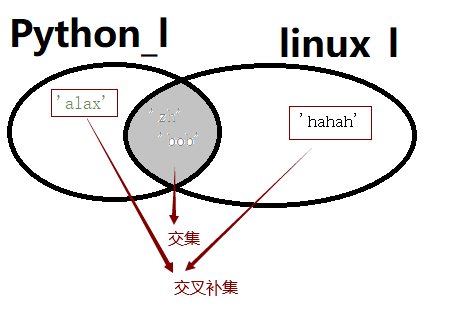
2、其他关系运算

（1）判断两个集合的交集是否为空  A.isdisjoint(B)

s1={'kk','bb','zz'}
s2={'kk','ss','aa'}
s3={1,2,3}
result1=s1.isdisjoint(s2)
print(result1)#运行结果：False  ——> 即交集不为空
result2=s1.isdisjoint(s3)
print(result2)#运行结果：True  -->即交集为空

（2）判断两个集合的包含关系

　　集合A>=B  A.issubset(B)       集合A<=B   A.issuperset(B)

s1={1,2,3}
s2={4,5,6,1,2,3}
result1=s1.issubset(s2)
print(result1)#运行结果：True
result2=s1.issuperset(s2)
print(result2)#运行结果：False
result3=s2.issuperset(s1)
print(result3)#运行结果：True

（3）更新  A.update(B)  

s1={1,2,5}
s2={7,8}
s1.update(s2)
print(s1)#运行结果：{1, 2, 5, 7, 8}

三、补充：

　　集合是可变类型，当定义不可变集合时，可使用s=frozenset(**)

s=frozenset('hello')
print(s)#运行结果：frozenset({'l', 'o', 'h', 'e'})
#不可进行添加删除等操作