集训考试题tents

题目描述
Pb 去郊游啦！他来到一块空地打算在这里搭一个帐篷。
但是,帐篷的四个支撑点不能在落在任何位置上,而只能落在一些固定点上。现在,他找到地面上有 N 个点可以支撑帐篷。（四个支撑点必须围成一个矩形） 他想知道依次每加多一个点，搭帐篷的方法数。
输入格式
第1行：一个整数N
第2行至N+1行：每行有两个整数的x, y作为一个点的坐标。
输出格式
共N行：第i行表示当前加入第i个点后可以搭帐篷的方案数。

这题的关键在于如何判断任意四个点是矩形。
在数学上，矩形的判定有4种方式
1.有三个角是直角的四边形是矩形；
2.对角线互相平分且相等的四边形是矩形；
3.有一个角为直角的平行四边形是矩形；
4.对角线相等的平行四边形是矩形。
于是显然我们可以看出来，第一种和第三种方法肯定时候超时的
而第二种和第四种，从本质上讲，我们在是实现时是一样的
于是现在的问题是我们要如何快速判断对角线相等且平分

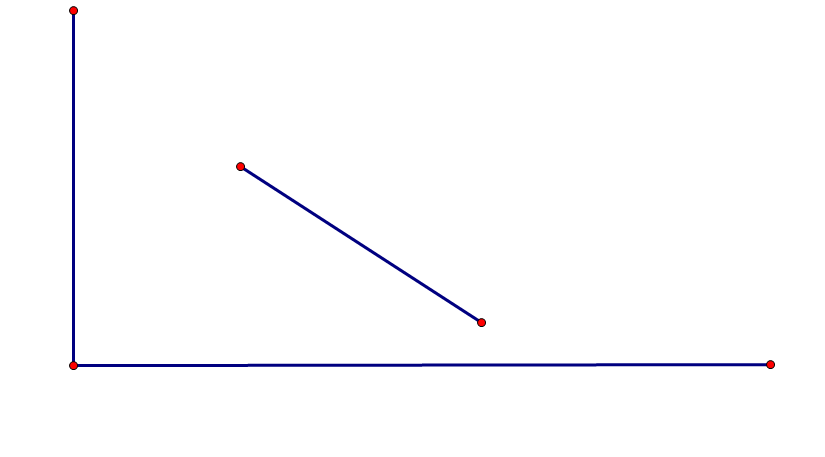
我们可以知道的是合法的对角线一定是这样的，对于一个矩形的两条对角线，我们可以知道他们的交叉点是相等的
而这个交叉点的横坐标是如图确定出一条对角线的两个点横坐标的和的一半，纵坐标同理
所以我们要先解决这个点，但是接着，问题出现了，只靠这一个信息是不够的。
我们目前有两个选择：
1.获取足够多的可以确定是矩形的信息
2.将三个点（矩形的两个顶点和对角线的中点）统一成一个值
显然我们肯定不愿意写第一种，因为很麻烦
所以我们可以利用第二种方式，于是我们很自然的想到了hash，为了保证答案的准确，我们只需要准备一个足够复杂和hash函数即可
而每一个hash过的数，我们用挂链法记录下来，若碰到了两个相等或是误差极小hash值，我们可以确定这四个点可以构成一个矩形，答案数加一
具体实现见代码

 #include<bits/stdc++.h>
 #define ll long long
 using namespace std;
 const int maxn = ;
 const int mod = ;
 const double cri = 0.0000001;
 struct enkidu {
     double x, y;
 }a[maxn];
 struct Shiki {//Ryougi
     double x, y, z;
     int net;
 }e[mod + ];
 int n, ans = ;
 int ha[mod + ], len = ;

 inline int read() {
     int x = , y = ;
     char ch = getchar();
     while(!isdigit(ch)) {
         if(ch == '-') y = -;
         ch = getchar();
     }
     while(isdigit(ch)) {
         x = (x << ) + (x << ) + ch - '';
         ch = getchar();
     }
     return x * y;
 }

 inline void insert(ll kk, double xx, double yy, double zz) {
     e[++len].x = xx;
     e[len].y = yy;
     e[len].z = zz;
     e[len].net = ha[kk];
     ha[kk] = len;
 } 

 inline bool check(double a, double b) {
     if(abs(a - b) < cri) return ;
     else return ;
 } 

 inline void hash(double x, double y, double z) {
     ll k = x * y + y * z + x * z + x + y + z + mod;
     if(k < ) k = -k;
     k %= mod;
     //cout << k << '\n';
     for(int i = ha[k]; i; i = e[i].net)
         if(check(x, e[i].x) && check(y, e[i].y) && check(z, e[i].z))
             ans++;
     insert(k, x, y, z);
 }

 int main() {
     n = read();
     for(int i = ; i <= n; ++i)
         a[i].x = read(), a[i].y = read();
     for(int i = ; i <= n; ++i) {
         double x, y, z;
         for(int j = ; j < i; ++j) {
             x = (a[i].x + a[j].x) / ;
             y = (a[i].y + a[j].y) / ;
             z =  ((a[i].x - a[j].x) * x + (a[i].y - a[j].y) * y) / (a[i].x + a[j].y);
             hash(x, y, z);
         }
         cout << ans << '\n';
     }
     return ;
 }

目前接到反映加实测，上面那份代码好像死了....我....天知道发生了什么....

下面随便摆一份Ac的（hash函数不同

 #include<bits/stdc++.h>
 #define ll long long
 using namespace std;
 const int maxn = ;
 const int mod = ;
 struct node {
     double x, y;
 }a[maxn];
 struct nn {
     double x, y, z;
     ll net;
 }e[mod + ];
 int n;
 int lin[mod + ];
 int tot = , ans = ;
 double x, y, z;

 inline bool pd(double a, double b) {
     if(abs(a - b) < 0.000000001) return ;
     return ;
 }

 inline void insert(double x, double y, double z, ll k) {
     e[++tot].x = x;
     e[tot].y = y;
     e[tot].z = z;
     e[tot].net = lin[k];
     lin[k] = tot;
 }

 inline void hash(double x, double y, double z) {
     ll k = x * y + y * z + x * z + x + y + z + mod;
     if(k < ) k = -k;
     k %= mod;
 //    cout << 'k' << ':' << k <<'\n';
     for(int i = lin[k]; i; i = e[i].net)
         if(pd(e[i].x, x) && pd(e[i].y, y) && pd(e[i].z, z))
             ans++;
     insert(x, y, z, k);
 }

 int main() {
 //    freopen("tents.in", "r", stdin);
 //    freopen("tents.out", "w", stdout);
     cin >> n;
     for(int i = ; i <= n; i++) {
         cin >> a[i].x >> a[i].y;
         for(int j = ; j < i; ++j) {
             x = (a[i].x + a[j].x) / ;
             y = (a[i].y + a[j].y) / ;
             z = (a[i].x - a[j].x) * (a[i].x - a[j].x) + (a[i].y - a[j].y) * (a[i].y - a[j].y);
             hash(x, y, z);
         }
         cout << ans << '\n';
     }
     fclose(stdin);
     fclose(stdout);
     return ;