上课总结-模电chapter 2
1.无明显失真时电压放大倍数——输出与输入电压的变化量之比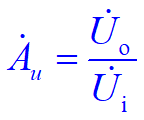
.无明显失真时 电流放大倍数——输出与输入电流的变化量之比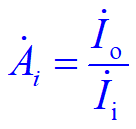
3.最大输出幅度
①无明显失真时最大输出电压(或最大输出电流)
②交流有效值(Uom 、Iom)或峰−峰值表示
4.非线性失真系数
所有谐波总量与基波成分之比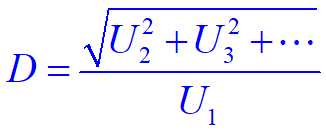
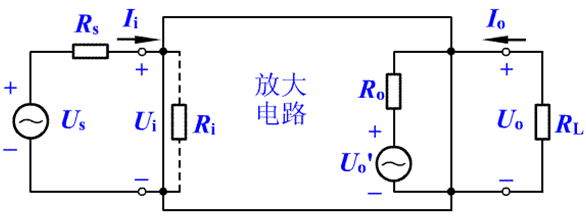
5.输入电阻
Ri大,电压索取强,减少Us功率负荷,放大电路对信号源索取的电流越小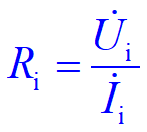
6.输出电阻
Ro小,放大电路的带负载能力强
7.通频带

8.最大输出功率与效率
输出不产生明显失真的最大输出功率 —— Pom(ŋ-效率Pv-直流电源消耗功率)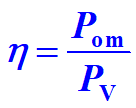
========================================================================
单管共发射极放大电路电路工作原理
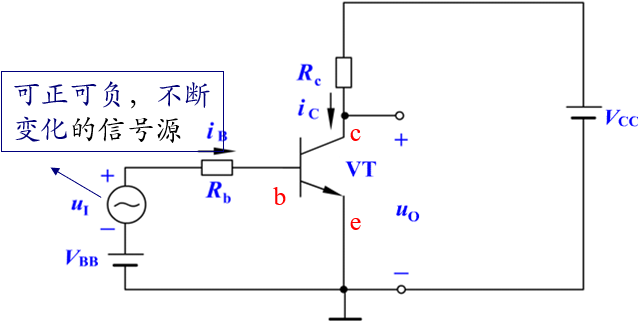
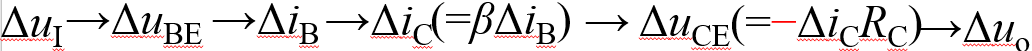
分压 分流 iC=βiB 分压 kvl
由上式可得:

==================================================================
放大电路的基本分析方法
1.顺序:先直流再交流
未输入信号时直流通路 加上信号时叫交流通路


2.图解法分析电路
①分析静态
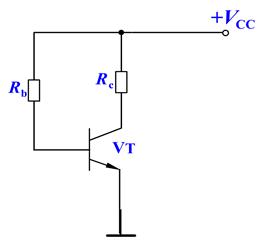
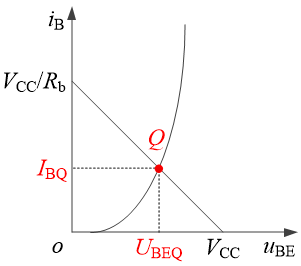
直流负载线用以确定静态工作点
②分析动态:变化量(交流分量)ΔuCE与Δic之间是线性关系
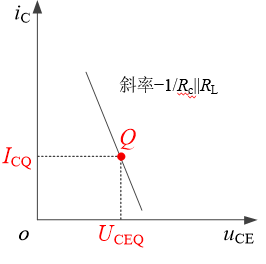
交流负载线描述动态时uCE与iC的关系
===================================================================
单管共射放大电路交流通路的微变等效
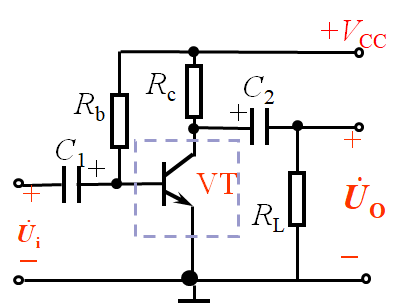
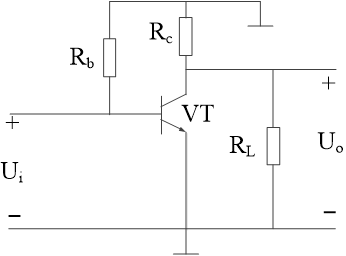
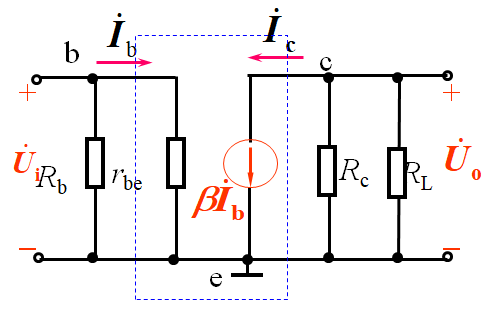
(1) (2) (3)
(1)==》(2)
其中电容相当于导线 Vcc变为0端电压
(2)==》 (3)
b和e间夹着rbe c和e夹着受控源
******************************************
其中 rbe 的求法:
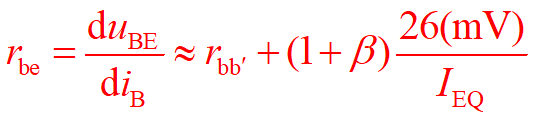
电压放大倍数:输出电压与输入电压之比
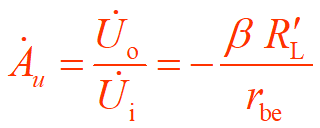
=================================
输入、输出电阻求法举例:
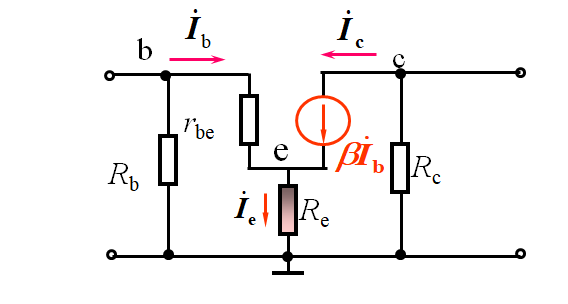
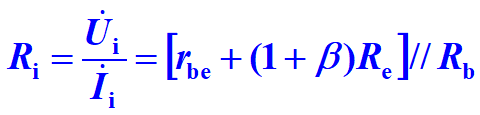

输入电阻 输出电阻
===================================================================
图解法与微变等效电路法优缺点比较
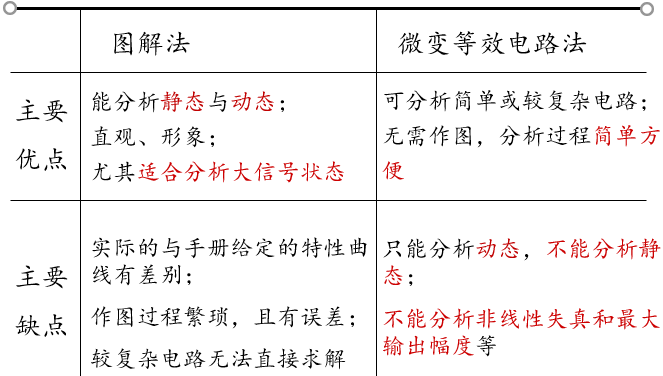
==================================================================================
典型例题分析
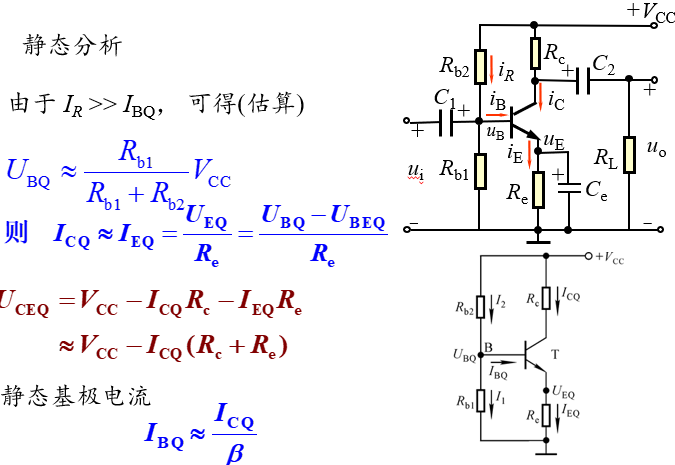

上课总结-模电chapter 2的更多相关文章
- 上课总结-模电chapter 1
Chapter 1 半导体器件 一.杂质半导体(N型半导体/P型半导体) N型 p型 特点 N型 将少量5价元素参入四价元素中==> 电子多 ==>电子为多子 p型 将少量3价元素参入四价 ...
- 模电&数电知识整理(不定期更新)
模电总复习之爱课堂题目概念整理 Chapter 1 1) 设室温情况下某二极管的反偏电压绝对值为1V,则当其反偏电压值减少100mV时,反向电流的变化是基本不发生变化. 2) 二极管发生击穿后,在击穿 ...
- 模电Multisim仿真Rb变化对Q点和电压放大倍数的影响
一.目的 研究Rb变化对Q点和Au的影响. 二.方法描述 仿真电路如下所示.晶体管采用FMMT5179其参数BF=133,RB=5Ω. (1)分別测量Rb=3MΩ和3.2MΩ时得UCEQ和Au.由于信 ...
- What is 软件工程
话说新的一学期,有一门叫软件工程的专业课,作为计算机科学与技术专业的学生,在上课前有几个问题 1.软件工程顾名思义是学软件,可是软件这个词范围还是挺大的,那到底学的是哪方面,是编程?设计APP?还是一 ...
- java第一节感受
第一节java课考试,感觉自从小学期和实习过了以后就等这个测试了,测试过了以后就是中秋节了,下周再上一节java又放国庆节了. 当时报软工的时候就早早地做好了心理准备,但是当亲身经历一遍后真的有了一种 ...
- 2017 Summary
几门课 基础电路与电子学 知道了一些二极管三极管的基本基本很基本的那种物理知识吧,但是毕竟我是从电信转专业过来的,所以说我内心就是逃避模电这样的课的.上课基本没听,后面只是死命复习了一周,考的还可以. ...
- 由ubuntu装好想到的
这篇不是技术文,有点唠叨的总结.不喜勿喷. 最近开始全面学ubuntu,一翻书回忆起本科没选但是去听了的Linux.当时看的还是楚广明的fedora教程,这多年过去综合很多人的说 法,fedora不稳 ...
- 风物长宜放眼量,人间正道是沧桑 - 一位北美 IT 技术人破局
引言 我对于本科时光的印象,还停留在那所普通 211 大学的建筑物之间,我坐在大学的时光长廊里,满眼望去,都是经历的过的故事.可毕业后回首,却很少有人能说,自己从来没有迷茫过.迷茫,仿佛就是一团乌云, ...
- 我是如何从通信转到Java软件开发工程师的?
我的读者里面有绝大部分都是在校学生,有本科的,也有专科的,我在微信里收到很多读者的提问,大部分问题都跟如何学习编程有关,有换专业自学的.有迷茫不知道如何学习的.有报培训班没啥效果的等等,我能感受到他们 ...
随机推荐
- dB2 索引相关
ALTER TABLE "XXXX"."tableA" PCTFREE 20 ; CREATE INDEX "schema"."X ...
- java多态介绍温故而知新
多态是同一个行为具有多个不同表现形式或形态的能力. 多态就是同一个接口,使用不同的实例而执行不同操作. 多态性是对象多种表现形式的体现. 现实中,比如我们按下 F1 键这个动作: 如果当前在 Flas ...
- 【树莓派智能门锁】使用脚本控制GPIO来开锁【4】
假定你已经通过此文章或者其他方式完成了树莓派的基本配置 [树莓派]RASPBIAN镜像初始化配置 我们通过VNC View连接到树莓派查看一下~ 1.更新一下基本的设置:更新一下源,把python-d ...
- 【知识碎片】python 篇
领域:运维 网站 游戏 搜索 嵌入式 C/S软件 Openstack二次开发 绿色版:Portable Python 面向对象.解释型动态语言 env python 切换版也好使,自己寻找系统中pyt ...
- collections、time和datetime模块
主要内容: 一.collections模块 二.time模块 三.datetime模块 1️⃣ collection模块 1.什么是collections模块.干什么用? collections模块 ...
- Leetcode:Divide Two Integers分析和实现
题目要求我们用一个32位整数整除另外一个整数,但是不允许我们使用除法,乘法和取模运算. 有趣的问题,下面说一下我的思路: 首先,先给出两个正整数除法运算的过程.假设a为被除数,而b为除数.在计算机中无 ...
- 【NOIP2008】传纸条
[描述] Description 小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题.一次素质拓展活动中,班上同学安排做成一个m行n列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就 ...
- EF删除,查询,Linq查询,Lambda查询,修改链接字符串
(1)//删除操作 public bool delete() { try { a_context = new AEntities(); b1 = new Table_1(); //删除只需要写主键就行 ...
- Python PyPI中国镜像
from:http://blog.makto.me/post/2012-11-01/pypi-mirror from:http://www.pypi-mirrors.org/ from:http:// ...
- Luogu 4159 [SCOI2009]迷路
BZOJ 1297 应当是简单题. 发现边权的数量很小,所以我们暴力把一个点拆成$9$个点,然后把$(x, i)$到$(x, i + 1)$连边,代表转移一次之后可以走回来:对于每一条存在的边$(i, ...
